Cette technologie est une invention qui risque de changer complètement les cartes dans tous les domaines, on peut déjà voir son application dans les domaines nécessitant un tier de confiance, comme la monnaie avec différents concept comme les cryptomonnaies même plus encore avec la monnaie libre qui est un système qui permet la création monétaire directement par les utilisateurs, il y aura aussi de grands changements dans la logistique, les sites permettant la mise en relation comme Airbnb, Uber, blabla car, etc.

Ses applications sont nombreuses, on peut même espérer organiser une démocratie, une vraie démocratie ou chaque citoyen pourrait faire valoir son vote. On peut même dans un futur proche avoir l’ambition de gérer la politique d’un politique à partir d’une blockchain et d’une IA. Beaucoup d’essais, de réflexions sont en cours.

Concernant l’article, Nous allons aborder la technologie de la blockchain par des exemples pour vous permettre de comprendre le nouveau paradigme qui est proposé grâce à cette technologie.

Ensuite nous prendrons le temps de comprendre la valeur ajoutée de la blockchain avec des exemples illustrés, ensuite nous expliquerons les concepts permettant de réaliser une blockchain et ses variantes possibles que ce soit les méthodes de consensus, les fonctions de hachage, etc. Nous détaillerons comment s’organise la sécurité d’une blockchain pour se prémunir des fraudes de type double dépense, création de transaction frauduleuse, etc.

Nous verrons par la suite les typiques de fonctionnement de la blockchain Bitcoin et Ethereum. Pour finir, nous développerons une application permettant de voter via une blockchain avec Ethereum et les fonctions du Dapp.

Vous serez enfin apte à comprendre tous les enjeux autour de la blockchain, son fonctionnement et tous les articles techniques de la presse informatique liés à la blockchain.

• Comprendre le fonctionnement de la monnaie et de la blockchain
  
• Comprendre le fonctionnement de Bitcoin
  
• Comprendre le fonctionnement d’Ethereum
  
• Développement d’application pour la Blockchain
  
• Construction d’une application pour la Blockchain

CHAPITRE 1 Introduction à la Blockchain

Blockchain est la nouvelle vague de perturbations qui a déjà commencé à repenser les interactions commerciales, sociales et politiques, et tout autre moyen d’échange de valeur. Encore une fois, il ne s’agit pas seulement d’un changement, mais d’un phénomène rapide qui est déjà en mouvement et annonce un nouveau paradigme. On compte déjà plus de 40 institutions financières de premier plan et de nombreuses entreprises au travers des industries qui ont commencé à explorer la blockchain pour réduire les coûts de transaction, accélérer le temps de transaction, réduire le risque de fraude, et d’éliminer l’intermédiaire ou les services intermédiaires dans tous un grand nombre de domaines. Certains essaient de réinventer les systèmes et services existants pour les amener à un nouveau niveau et aussi trouver de nouveaux types d’offres de services et d’autres réinvente leurs métiers au travers de la blockchain.

Nous couvrirons la blockchain plus en détail tout au long de l’article. Vous pouvez suivre les chapitres sur la barre à droite sur la blockchain ou choisissez seulement ceux qui vous sont pertinents. Ce chapitre explique ce qu’est la blockchain, comment elle a évolué, et son importance dans le monde d’aujourd’hui avec quelques utilisations et cas d’utilisation. Commençons par détailler au travers de son histoire la blockchain.

Histoire de Blockchain

L’une des premières perturbations numériques connues qui a jeté les bases d’Internet a été le TCP/IP (Protocole de contrôle de la transmission/Protocole Internet) dans les années 1970. Avant TCP/IP, c’était l’ère de la commutation de circuit, qui exigeait une connexion dédiée entre deux parties pour que la communication se produise. TCP/IP a mis au jour sa conception de commutation de paquets, qui était plus ouverte et peer-to-peer sans avoir besoin de préétablir une ligne dédiée entre les parties.

Lorsque l’Internet a été rendu accessible au public par l’entremise du World Wide Web (WWW) au début des années 1990, il était censé être plus ouvert et plus égalitaire. C’est parce qu’il a été construit au sommet de l’ouvert et décentralisé TCP / IP. Lorsque toute nouvelle technologie, en particulier révolutionnaire, frappe le marché, soit elles s’estompent d’elles-mêmes, soit elles créent un tel impact qu’elles deviennent la norme acceptée. Les gens se sont adaptés à la révolution WWW et ont tiré parti des avantages qu’elle avait à offrir de toutes les manières possibles. En conséquence, le World Wide Web a commencé à se dessiner d’une manière qui n’aurait peut-être pas été la façon exacte dont il a été imaginé. Il aurait pu être plus ouvert, plus accessible et plus égalitaire. Beaucoup de nouvelles technologies et d’entreprises ont commencé à s’appuyer sur elle et elle est devenue ce qu’elle est aujourd’hui, plus centralisée. Lentement et graduellement, les gens s’habituent à ce que la technologie offre.

Examinons de plus près le système bancaire et son évolution. À partir de l’époque du système de troc jusqu’aux monnaies fiduciaires, il n’y avait pas de réelle différence entre une transaction et son règlement parce qu’il ne s’agissait pas de deux entités distinctes. Par exemple, si Alice devait payer 10 € à Bob, elle remettait simplement un billet de 10 € à Bob et la transaction s’effectuait. Aucune banque n’était nécessaire pour débiter 10 € du compte d’Alice et de créditer de la même chose sur le compte de Bob ou d’établir un système de confiance pour s’assurer qu’Alice ne trompe pas Bob. Toutefois, les transactions directes avec quelqu’un qui n’est pas physiquement présent à proximité restaient difficiles. Ainsi, les systèmes bancaires ont évolué avec beaucoup plus d’offres de services et ont permis des transactions dans tous les coins du monde. Avec l’aide d’Internet, la géographie n’était plus une limitation et les services bancaires sont devenus plus faciles que jamais. Pas seulement les banques d’ailleurs : l’Internet a facilité de nombreux types différents d’échange de valeur sur le web.

La technologie a permis à quelqu’un de l’Inde de faire une transaction monétaire avec quelqu’un au Royaume-Uni, mais avec un certain coût. Il faut des jours pour régler de telles transactions et elles sont coûteuses. Une banque était toujours nécessaire pour imposer la confiance et assurer la sécurité de telles transactions entre deux parties ou plus. Et si la technologie pouvait permettre la confiance et la sécurité sans ces systèmes intermédiaires et centralisés ?

D’une manière ou d’une autre, cette partie (de la technologie imposant la confiance) manquait à l’appel, ce qui a entraîné le développement de systèmes centralisés tels que les banques, les services d’entiercement, les chambres de compensation, les bureaux d’enregistrement et de nombreuses autres institutions de ce type. Au sein de l’UE, on peut le modéliser par le système SEPA et l’une de ses briques les TARGET.

La Blockchain quant à elle, s’avère être cette pièce manquante du puzzle de la révolution Internet qui facilite un système sans confiance d’une manière cryptographiquement sécurisée.

Satoshi Nakamoto, le pseudonyme que le monde connaît, a dû sentir que les systèmes monétaires n’ont pas été touchés par la révolution technologique depuis les années 1980. Les banques ont formé les institutions centralisées qui maintenaient les registres des transactions, gouvernaient les interactions, faisaient respecter la confiance et la sécurité et réglementaient l’ensemble du système. L’ensemble du commerce repose sur ces institutions financières, qui servent de tiers de confiance pour traiter les paiements. La médiation des institutions financières augmente les coûts et le temps de règlement d’une transaction, et limite également la taille des transactions. La médiation était nécessaire pour régler les différends, mais cela signifiait que la transaction complètement non réversible n’était jamais possible. Il en a résulté une situation où la confiance était nécessaire pour que quelqu’un interagisse avec un autre. Certes, ce système bureaucratique a dû changer pour suivre la transformation numérique attendue de l’économie.

Ainsi, Satoshi a inventé une crypto-monnaie appelée Bitcoin qui a été activée par la technologie sous-jacente – blockchain. Bitcoin n’est qu’un cas d’utilisation monétaire de la blockchain qui s’attaque à la faiblesse inhérente des modèles basés sur la confiance. Nous allons approfondir les fondamentaux des Bitcoins et de la blockchain dans cet article.

Qu’est-ce que la Blockchain ?

L’Internet a révolutionné de nombreux aspects de la vie, de la société et des affaires. Cependant, nous avons appris dans la section précédente que la façon dont les gens et les organisations exécutent des transactions les uns avec les autres n’a pas beaucoup changé au cours des deux dernières décennies. Blockchain est considéré comme le composant qui complète le puzzle Internet et le rend plus ouvert, plus accessible et plus fiable.

Pour comprendre la blockchain, il faut la comprendre à la fois d’un point de vue commercial et technique. Comprenons d’abord dans un contexte de transaction d’affaires pour obtenir le “quoi” de celui-ci, puis nous examinerons la technicité pour comprendre le “comment” de celui-ci dans les chapitres suivants.

Blockchain est un système d’enregistrements pour traiter la valeur (pas seulement l’argent !) d’une manière peer-to-peer. Ce que cela signifie, c’est qu’il n’y a pas besoin d’un intermédiaire de confiance comme les banques, les courtiers ou d’autres services d’entiercement pour servir de tiers de confiance. Par exemple, si Alice paie à Bob 10 €, pourquoi passerait-elle par une banque ? Jetez un œil à la figure 1-1.

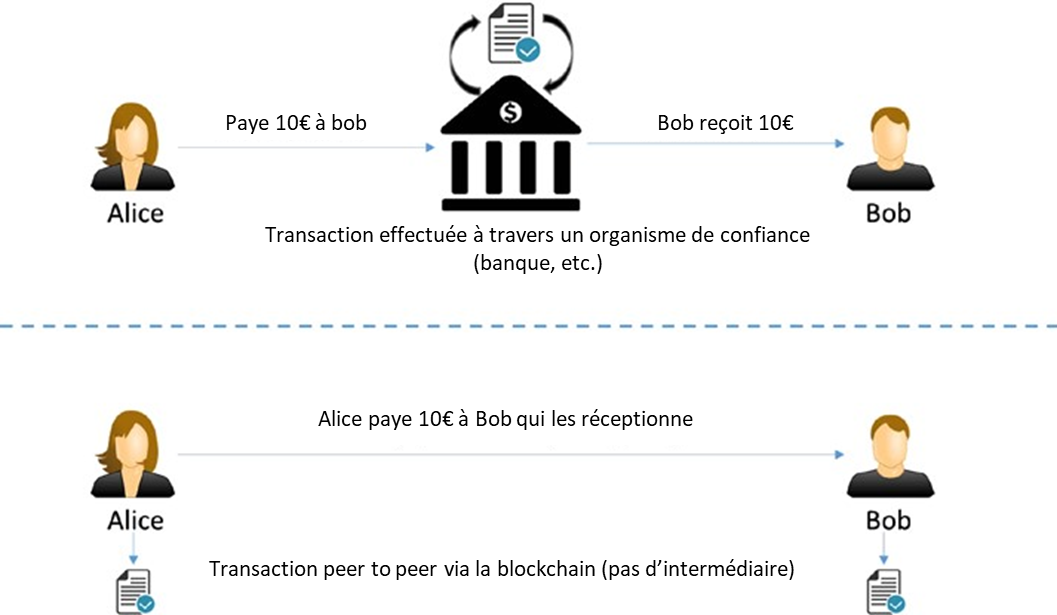
Figure 1-1. Transaction par un intermédiaire de confiance par rapport à la transaction peer-to-peer

Examinons un exemple différent maintenant. Une transaction d’actions typique se produit en quelques secondes, mais son règlement prend des semaines (voir les soldes Target). Est-il souhaitable en cette ère numérique ? Certainement pas ! La figure 1-2 illustre la situation actuelle.

Figure 1-2. Opérations d’actions par l’intermédiaire d’une chambre de compensation intermédiaire

Si quelqu’un veut acheter des actions d’une entreprise ou d’une personne, il peut simplement l’acheter directement auprès d’eux avec un règlement instantané, sans avoir besoin de courtiers, de chambres de compensation ou d’autres institutions financières entre les deux. Une solution décentralisée et peer-to-peer à une telle situation peut être représentée comme dans la figure 1-3.

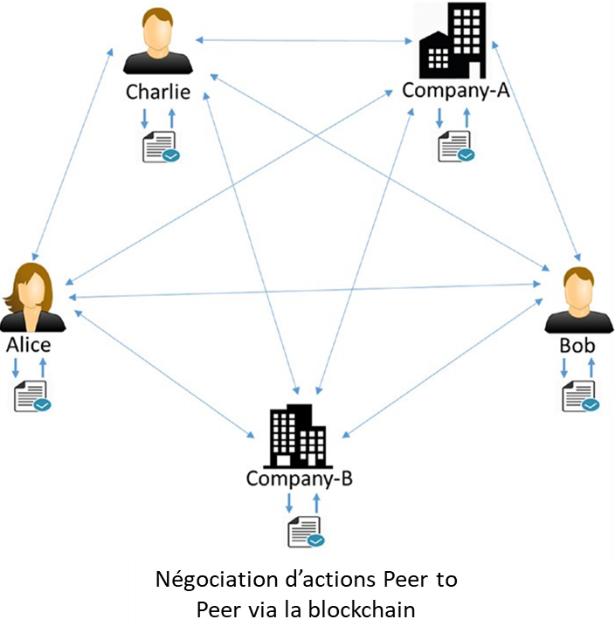
Figure 1-3. Négociation d’actions peer-to-peer

Notons que les transactions et les règlements ne sont pas deux entités différentes dans un paramètre blockchain ! Les transactions sont analogues, par exemple, aux transactions en monnaie fiduciaire ou si quelqu’un paie un autre billet de 10 €, il ne le possède plus et ce billet de 10 € est physiquement transféré au nouveau propriétaire.

Maintenant que vous comprenez la blockchain d’un point de vue fonctionnel, à un niveau élevé, examinons-la un peu techniquement, et la raison de la nommer “blockchain” devient plus claire. Nous verrons “Qu’est-ce” qu’il est en techniquement et laisser le “Comment” du fonctionnement au chapitre 2.

Lisez les énoncés suivants et ne vous inquiétez pas si les concepts ne permettent pas encore votre compréhension complète. Vous voudrez peut-être le revoir, mais soyez patient jusqu’à ce que vous ayez fini de lire cet article.

• Blockchain est un système peer-to-peer de transactions de valeurs sans tiers de confiance entre les deux.
• Il s’agit d’un registre partagé, décentralisé et ouvert des transactions. Cette base de données de registre est reproduite sur un grand nombre de nœuds (les nœuds en informatique font référence à un serveur).
• Cette base de données de registre est une base de données d’ajout de transactions uniquement et ne peut pas être modifiée ou altérée. Cela signifie que chaque entrée est une entrée permanente. Toute nouvelle entrée sur elle est reflétée sur toutes les copies des bases de données hébergées sur différents nœuds. (Mais comme on dit il ne faut jamais dire jamais, il existe dans certains cas des possibilités d’altérer une transaction, mais pour cela il faut contrôler plus de 50 % des nœuds du réseau, nous ne ferons pas état de ce cas dans cet article.)
• Il n’est pas nécessaire que des tiers de confiance servent d’intermédiaires pour vérifier, sécuriser et régler les transactions.
• Il s’agit d’une autre couche au-dessus de l’Internet et peut coexister avec d’autres technologies Internet.
• Juste la façon dont TCP/ IP a été conçu pour atteindre un système ouvert, la technologie blockchain a été conçue pour permettre une véritable décentralisation. Dans un effort pour le faire, les créateurs de Bitcoin l’ont fait de façon « open-source » afin qu’elle puisse inspirer de nombreuses applications décentralisées.

Une blockchain typique ressemble à ce qui est indiqué dans la figure 1-4.

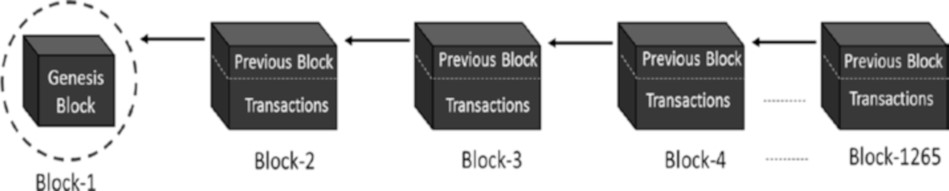
Figure 1-4. La structure de données blockchain

Chaque nœud sur le réseau blockchain a une copie identique de la blockchain montrée dans la figure 1-4, où chaque bloc est une collection de transactions, d’où le nom. Comme vous pouvez le voir, il y a deux parties principales dans chaque bloc. La partie “en-tête” (Header en anglais) renvoie au bloc précédent de la chaîne. Ce que cela signifie, c’est que chaque en-tête de bloc contient le hash du bloc précédent de sorte que personne ne peut modifier une transaction dans le bloc précédent. Nous examinerons plus en détail ce concept dans les chapitres suivants. L’autre partie d’un bloc est le “contenu” (Body content en anglais) qui a une liste validée des transactions, leurs montants, les adresses des parties concernées, et quelques détails supplémentaires. Ainsi, étant donné le dernier bloc, il est possible d’accéder à tous les blocs précédents dans une blockchain.

Prenons un exemple pratique et voyons comment les transactions ont lieu et le grand livre (ledger en anglais) est mis à jour à travers le réseau, pour voir comment ce système fonctionne :

Supposons qu’il y ait trois candidats — Alice, Bob et Charlie — qui effectuent des transactions monétaires l’un d’entre eux sur un réseau de blockchain. Passons en revue les transactions étape par étape pour comprendre les fonctionnalités ouvertes et décentralisées de la blockchain.

Étape 1 :

Supposons qu’Alice avait 50€ avec elle, ce qui est la genèse de toutes les transactions et que chaque nœud en est conscient, comme le montre la figure 1-5.

Figure 1-5. Le bloc de genèse

Étape 2 :

Alice fait une transaction en payant 20 $ à Bob. Observez comment la blockchain est mise à jour à chaque nœud, comme le montre la figure 1-6.

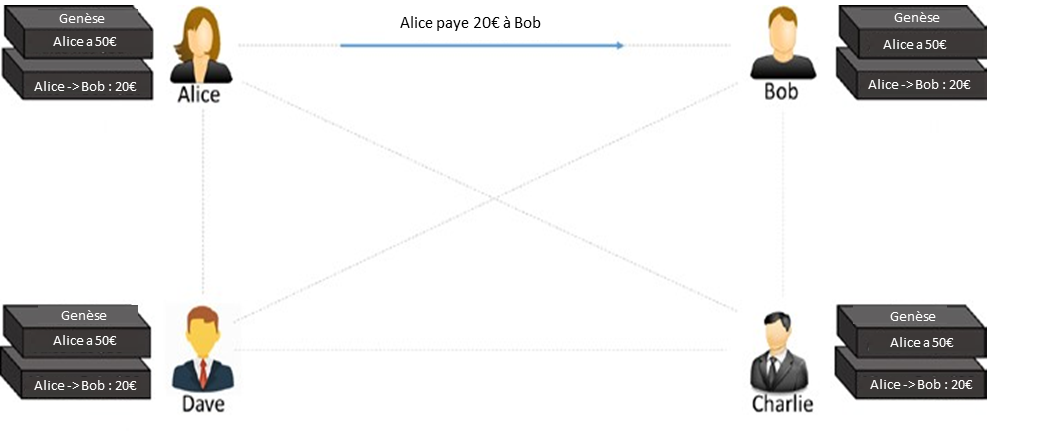
Figure 1-6. La première transaction

Étape 3 :

Bob fait une autre transaction en payant 10 $ à Charlie et la blockchain est mise à jour comme indiqué dans la figure 1-7.

Figure 1-7. La deuxième transaction

Notons que les données de transaction dans les blocs sont immuables. Toutes les transactions sont totalement irréversibles. Tout changement entraînerait une nouvelle transaction, qui serait validée par tous les nœuds contributeurs. Chaque nœud a sa propre copie de la blockchain.

S’il y a beaucoup de questions qui surgissent dans votre esprit, telles que « Et si Alice paye le même montant à Dave pour doubler le même montant, ou si elle fait un paiement sans avoir assez de fonds dans son compte ? », « Comment la sécurité est-elle assurée ?, et ainsi de suite! Nous allons aborder ces détails dans les chapitres suivants.

Systèmes centralisés vs décentralisés

La raison même pour laquelle nous pensons le débat sur la centralisation par rapport à la décentralisation est que la blockchain est conçue pour être décentralisée, défiant la conception centralisée. Cependant, les sternes décentralisées et centralisées ne sont pas toujours claires. Ils sont très mal définis et trompeurs dans de nombreux endroits. La raison en est qu’il n’y a presque pas de système purement centralisé ou décentralisé.

Qu’est-ce qu’un système distribué alors ? Juste pour la discussion actuelle, nous allons le comprendre et ensuite le retirer de la liste. Veuillez noter que si un système est centralisé ou décentralisé, il peut toujours être distribué. Un système distribué centralisé est un système dans lequel il y a, par exemple, un nœud maître chargé de décomposer les tâches ou les données et de distribuer la charge à travers les nœuds. D’autre part, un système distribué décentralisé est un système où il n’y a pas de nœud ” maître ” en tant que tel et pourtant le calcul peut être distribué. Blockchain est un exemple de ce genre, et nous allons examiner de nombreuses représentations schématiques de celui-ci plus tard dans l’article. La figure 1-8 est une représentation de la façon dont un système distribué centralisé peut fonctionner.

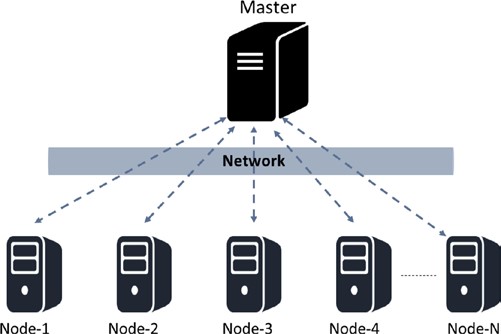
Figure 1-8. Un système distribué avec contrôle centralisé

Cette représentation est similaire à la mise en œuvre Hadoop, à titre d’exemple. Bien que le calcul est plus rapide dans de telles conceptions en raison de l’informatique distribuée, il souffre également de limitations dues à la centralisation.

Reprenons notre discussion sur la centralisation par rapport à la décentralisation. Il est extrêmement important de noter que pour qu’un système soit centralisé/décentralisé, il ne se limite pas à l’architecture technique. Ce que je dis, c’est qu’un système peut être centralisé ou décentralisé techniquement, mais qu’il ne l’est peut-être pas de façon logique ou politique. Jetons un coup d’œil à ces différentes perspectives pour être en mesure de concevoir un système correctement basé sur l’exigence :

Architecture technique : Un système peut être centralisé ou décentralisé du point de vue de l’architecture technique. Ce que nous considérons est combien d’ordinateurs physiques (ou nœuds) sont utilisés pour concevoir un système, combien de défaillances de nœuds, il peut soutenir avant que l’ensemble du système ne tombe en panne, etc.

Perspective politique : Cette perspective indique le contrôle qu’un individu, ou un groupe de personnes, ou une organisation dans son ensemble a sur un système. Si les ordinateurs du système sont contrôlés par eux, alors le système est naturellement centralisé. Cependant, si aucun individu ou groupe spécifique ne contrôle le système et que tout le monde a des droits égaux sur le système, alors c’est un système décentralisé dans un sens politique !

Perspective logique : Un système peut être logiquement centralisé ou décentralisé en fonction de son apparence, qu’il soit centralisé ou décentralisé techniquement ou politiquement. Une autre analogie pourrait être que si vous coupez verticalement un système (par exemple des dispositifs informatiques) en deux avec chaque moitié ayant des fournisseurs de services et des consommateurs, s’ils peuvent fonctionner comme des unités indépendantes, ils sont décentralisés et centralisés autrement.

Toutes les perspectives susmentionnées sont cruciales dans la conception d’un système de la vie réelle et son appellation de centraliser ou décentraliser. Discutons de quelques-uns des exemples mélangeant ces perspectives pour dissiper toute confusion que vous pourriez avoir :

• Si vous regardez les entreprises, elles sont architecturalement centralisées (un siège social), elles sont politiquement centralisées (régies par un PDG ou le conseil d’administration), et elles sont logiquement centralisées aussi. (Vous ne pouvez pas vraiment les diviser en deux.)
• Notre langage de communication est décentralisé sous tous les angles, tant sur le plan architectural, politique que logique. Pour que deux personnes communiquent entre elles, en général, leur langue n’est ni politiquement influencée ni logiquement dépendante du langage de communication des autres.
• Les systèmes torrent tels que BitTorrent sont également décentralisés sous tous les angles. N’importe quel nœud peut être un fournisseur ou un consommateur, donc même si vous coupez le système en deux, il soutient toujours.
• Le Réseau de livraison de contenu, quant à lui, est architecturalement décentralisé, logiquement aussi décentralisé, mais il est politiquement centralisé parce qu’il appartient à des entreprises. Un exemple est Amazon CloudFront.
• Considérons la blockchain maintenant. L’objectif de la blockchain était de permettre la décentralisation. Ainsi, il est architecturalement décentralisé par la conception. En outre, il est décentralisé d’un point de vue politique, car personne ne le contrôle. Cependant, il est logiquement centralisé, car il y a un état commun convenu et l’ensemble du système se comporte comme un seul ordinateur global.

Examinons ces termes séparément et ayons une vision comparative pour être en mesure d’apprécier pourquoi la blockchain est décentralisée par la conception.

Systèmes centralisés

Comme son nom l’indique, un système centralisé a un contrôle centralisé avec toute autorité administrative. Ces systèmes sont faciles à concevoir, maintenir, imposer la confiance et gouverner, mais souffrent de nombreuses limitations inhérentes, comme suit :

Ils ont un point central d’échec, donc sont moins stables.

• Ils sont plus vulnérables aux attaques et donc moins sécurisés.
• La centralisation du pouvoir peut conduire à des opérations contraires à l’éthique.
• L’évolutivité est difficile la plupart du temps.

Un système centralisé typique peut apparaître comme indiqué à la figure 1-9.

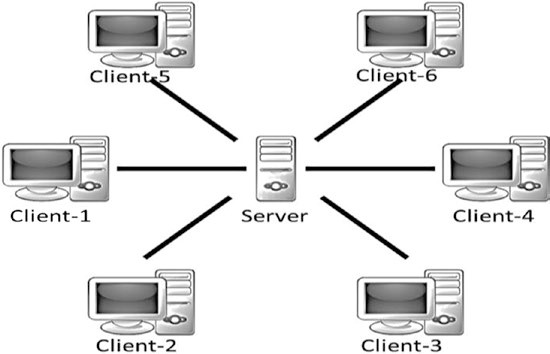
Figure 1-9. Un système centralisé

Systèmes décentralisés

Comme son nom l’indique, un système décentralisé n’a pas de contrôle centralisé et chaque nœud a une autorité égale. De tels systèmes sont difficiles à concevoir, à maintenir, à gouverner ou à imposer la confiance. Cependant, ils ne souffrent pas des limites des systèmes centralisés conventionnels. Les systèmes décentralisés offrent les avantages suivants :

• Ils n’ont pas un point central d’échec, donc plus stable et tolérant aux défauts
• Ils sont résistants aux attaques, comme il n’existe aucun point central, il est difficile d’en prendre le contrôle et est donc plus sécurisé (difficile n’est pas impossible, contrôler 50 % des nœuds pourraient permettre la falsification, mais ceci n’est évidemment pas préférable pour les possesseurs de nœuds, puisque les acteurs de cette blockchain en perdraient la confiance et la valeur inhérente au service ne ferait que baisser. Il est donc préférable pour tous les acteurs que ce cas ne se produisent pas.)
• système symétrique avec une autorité égale à tous, donc moins de portée d’opérations contraires à l’éthique et généralement de nature démocratique

Un système décentralisé typique peut apparaître comme indiqué à la figure 1-10.

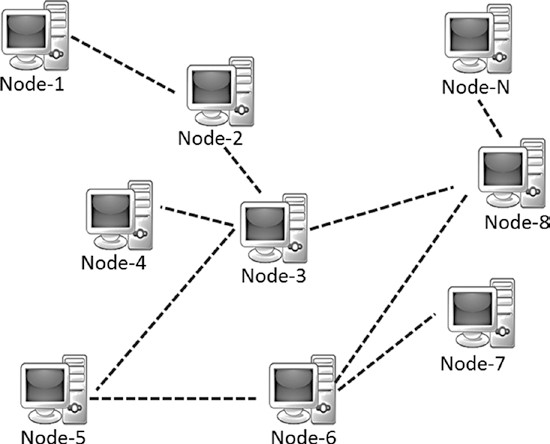
Figure 1-10. Un système décentralisé

Veuillez noter qu’un système distribué peut également être décentralisé. Un exemple serait la blockchain! Cependant, contrairement aux systèmes distribués courants, la tâche n’est pas subdivisée et déléguée aux nœuds, car il n’y a pas de maître qui ferait cela dans la blockchain. Les nœuds contributifs ne fonctionnent pas sur une partie de l’œuvre, mais plutôt sur les nœuds intéressés (ou ceux choisis au hasard) qui exécutent l’ensemble de l’œuvre. Un système décentralisé et distribué typique, qui est en fait un système peer-to-peer, peut apparaître comme indiqué à la figure 1-11.

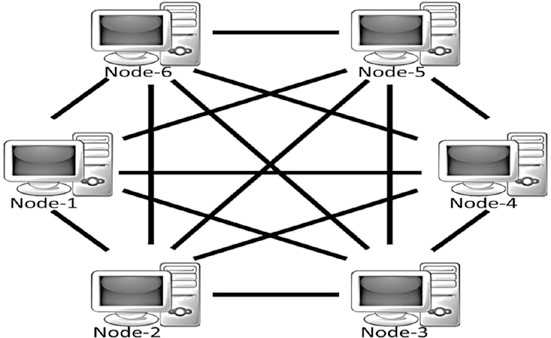
Figure 1-11. Un système décentralisé et peer-to-peer

Couches de Blockchain

Au fait que d’après cette écriture, les variantes de la blockchain publique comme Ethereum sont en train de mûrir, et la construction d’applications complexes au-dessus de ces blockchains n’est peut-être pas une bonne idée. Gardez à l’esprit que la blockchain n’est jamais seulement un morceau de technologie, mais une combinaison de principes d’affaires, l’économie, la théorie des jeux, la cryptographie et l’ingénierie informatique. La plupart des applications du monde réel sont de nature assez complexe, et il est conseillé de construire des solutions blockchain à partir de zéro.

Le but de cette section est seulement de vous fournir une vue à vol d’oiseau de diverses couches de blockchain, et d’approfondir les principes fondamentaux dans les chapitres suivants. Pour commencer, rappelons-nous simplement notre compréhension de base de la pile de protocole TCP/IP. L’approche en couches dans la pile TCP/IP est en fait une norme pour atteindre un système ouvert. Avoir des couches d’abstraction aide non seulement à mieux comprendre la pile, mais aide également à construire des produits qui sont conformes à la pile pour atteindre un système ouvert. En outre, avoir les couches abstraites les unes des autres rend le système plus robuste et plus facile à maintenir. Toute modification apportée à l’une ou l’autre des couches n’affecte pas les autres couches. Encore une fois, l’analogie TCP/IP ne doit pas être confondu avec les couches blockchain. TCP/IP est un protocole de communication que chaque application Internet utilise, tout comme la blockchain.

Entrez dans la blockchain. Il n’existe pas encore de normes mondiales convenues qui sépareraient clairement les composants de la blockchain en couches distinctes. Une architecture hétérogène en couches est nécessaire, mais pour l’instant c’est encore dans l’avenir. Ainsi, nous allons essayer de formuler des couches blockchain pour être en mesure de mieux comprendre la technologie et de construire une analogie comparative entre des centaines de variantes blockchain / Cryptocurrency sur le marché. Jetez un coup d’œil à la représentation de haut niveau et en couches de la blockchain dans la figure 1-12.

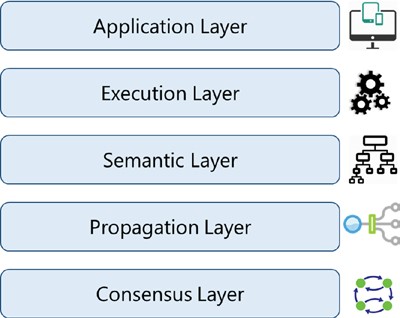
Figure 1-12. Différentes couches de blockchain

Vous vous demandez peut-être pourquoi cinq couches et pourquoi pas plus de couches granulaires, ou moins de couches. De toute évidence, il ne peut y avoir trop ou trop peu de couches ; il s’agira d’un compromis entre complexité, robustesse, adaptabilité, etc., pour n’en nommer que quelques-unes. Le but n’est pas vraiment de normaliser la technologie blockchain, mais de construire une meilleure compréhension.

Gardons à l’esprit que toutes ces couches sont présentes sur tous les nœuds.

Dans le chapitre 6 de cet article, nous allons construire une application décentralisée à partir de zéro et apprendre comment la blockchain fonctionne sur toutes ces couches avec un cas d’utilisation pratique.

Couche d’application

En raison des caractéristiques de la blockchain, telles que l’immuabilité des données, la transparence entre les participants, la résilience contre les attaques contradictoires, etc., il existe de multiples applications en cours de construction. Certaines applications sont juste construites dans la couche d’application, en tenant pour acquis toute « saveur » disponible de blockchain, et certaines applications sont construites dans la couche d’application et sont entrelacés avec d’autres couches dans la blockchain. C’est la raison pour laquelle la couche d’application doit être considérée comme faisant partie de la blockchain.

Il s’agit de la couche où vous codez les fonctionnalités souhaitées et en faites une application pour les utilisateurs finaux. Il s’agit généralement d’une pile technologique traditionnelle pour le développement de logiciels tels que les constructions de programmation côté client, scripts, API, « Framework » de développement, etc. Pour les applications qui traitent la blockchain comme un backend, ces applications peuvent avoir besoin d’être hébergées sur certains serveurs Web et qui pourraient nécessiter le développement d’applications Web, la programmation côté serveur, et les API, etc. Idéalement, les bonnes applications blockchain n’ont pas de modèle client-serveur, et il n’y a pas de serveurs centralisés pour l’accès du client, qui est juste la façon dont Bitcoin fonctionne.

Vous avez probablement entendu parler ou déjà appris au sujet des réseaux hors chaîne (« off-chain networks »). L’idée est de construire des applications qui n’utiliserait pas la blockchain pour tout et n’importe quoi, mais l’utiliser à bon escient. En d’autres termes, ce concept est de s’assurer que la gestion de lourdes tâches est faite à la couche application, ou les exigences de stockage volumineux sont pris en charge hors de la chaîne de sorte que la blockchain de base est légere et efficace et le trafic réseau n’est pas trop important.

Couche d’exécution

La couche d’exécution est l’endroit où les exécutions des instructions ordonnées par la couche d’application ont lieu sur tous les nœuds d’un réseau blockchain. Les instructions peuvent être des instructions simples ou un ensemble d’instructions multiples sous la forme d’un contrat intelligent (le smart contract en anglais). Dans les deux cas, un programme ou un script doit être exécuté pour assurer l’exécution correcte de la transaction. Tous les nœuds d’un réseau blockchain doivent exécuter les programmes/scripts de manière indépendante. Avec une exécution déterministe des programmes/scripts sur le même ensemble d’entrées et avec les mêmes conditions produit toujours la même sortie sur tous les nœuds, ce qui permet d’éviter les incohérences.

Dans le cas des Bitcoins, ce sont des scripts simples qui ne sont pas Turing complet et ne permettent que quelques ensembles d’instructions. Ethereum et Hyperledger, d’autre part, permettent des exécutions complexes. Le code d’Ethereum ou ses contrats intelligents écrits en solidité est compilé sur Bytecode ou Machine Code qui est exécuté sur sa propre machine virtuelle Ethereum.

Hyperledger a une approche beaucoup plus simple pour ses contrats intelligents à code de chaîne. Il prend en charge l’exécution des codes machine compilés à l’intérieur des images docker, et prend en charge plusieurs langages de haut niveau tels que le Java et le Go.

Couche sémantique

La couche sémantique est une couche logique parce qu’il y a un ordre dans les transactions et les blocs. Une transaction, valide ou invalide, a un ensemble d’instructions qui passe par la couche d’exécution mais est validée dans la couche sémantique.

Si c’est Bitcoin, alors si l’on dépense une transaction légitime, s’il s’agit d’une attaque à double dépense, si l’on est autorisé à faire cette transaction, etc, sont validés dans cette couche. Vous apprendrez dans les chapitres suivants que les Bitcoins sont en fait présents sous forme de transactions représentant l’état du système. Pour pouvoir dépenser un Bitcoin, vous devez consommer une ou plusieurs transactions précédentes et il n’y a aucune notion de comptes. Cela signifie que lorsqu’une personne effectue une transaction, elle utilise l’une des transactions précédentes où elle a reçu au moins le montant qu’elle dépense actuellement. Cette transaction doit être validée par tous les nœuds en traversant les transactions précédentes pour voir s’il s’agit d’une transaction légitime. Ethereum, d’autre part, a le système de comptes. Cela signifie que le compte de celui qui effectue la transaction et celui de celui qui la reçoit sont mis à jour.

Dans cette couche, les règles du système peuvent être définies, telles que les modèles de données et les structures. Il pourrait y avoir des situations qui sont un peu plus complexes par rapport aux transactions simples. Les ensembles d’instructions complexes sont souvent codés dans des contrats intelligents. L’état du système est mis à jour lorsqu’un contrat intelligent est invoqué lors de la réception d’une transaction. Un contrat intelligent est un type spécial de compte qui a le code exécutable et les états privés. Un bloc contient généralement un tas de transactions et quelques contrats intelligents. Les structures de données telles que l’arbre de Merkle sont définies dans cette couche avec la racine de Merkle dans l’en-tête de bloc pour maintenir une relation entre les en-têtes de bloc et l’ensemble des transactions dans un bloc (généralement le stockage de la valeur clé sur le disque). En outre, les modèles de données, les modes de stockage, dans le traitement basé sur la mémoire/disque, etc. peuvent être définis dans cette couche logique.

En dehors de ce qui précède, c’est la couche sémantique qui définit la façon dont les blocs sont liés les uns aux autres. Chaque bloc dans une blockchain contient le hash du bloc précédent, jusqu’au bloc de genèse. Bien que l’état final de la blockchain soit atteint par les contributions de toutes les couches, le lien des blocs les uns avec les autres doit être défini dans cette couche. Selon le cas d’utilisation, vous pouvez coder une fonctionnalité supplémentaire dans cette couche.

Couche de propagation

Les couches précédentes étaient plus d’un phénomène individuel : pas beaucoup de coordination avec d’autres nœuds dans le système. La couche de propagation est la couche de communication peer-to-peer qui permet aux nœuds de se découvrir les uns les autres, et de parler et de synchroniser les uns avec les autres en ce qui concerne l’état actuel du réseau. Lorsqu’une transaction est effectuée, nous savons qu’elle est diffusée sur l’ensemble du réseau. De même, lorsqu’un nœud veut proposer un bloc valide, il est immédiatement propagé à l’ensemble du réseau afin que d’autres nœuds puissent s’y appuyer, le considérant comme le dernier bloc. Ainsi, la propagation transaction/bloc dans le réseau est définie dans cette couche, ce qui assure la stabilité de l’ensemble du réseau. De par sa conception, la plupart des blockchains sont conçues de telle sorte qu’elles envoient immédiatement une transaction/bloc à tous les nœuds auxquels elles sont directement connectées, lorsqu’elles font la connaissance d’une nouvelle transaction/bloc.

Dans le réseau Internet asynchrone, il y a souvent des problèmes de latence pour la propagation des transactions ou des blocs. Certaines propagations se produisent en quelques secondes et d’autres prennent plus de temps, selon la capacité des nœuds, la bande passante réseau, et quelques facteurs de plus.

Couche de consensus

La couche de consensus est généralement la couche de base pour la plupart des systèmes blockchain. Le but principal de cette couche est d’obtenir tous les nœuds d’accord sur un état cohérent du grand livre. Il pourrait y avoir différentes façons de parvenir à un consensus entre les nœuds, selon le cas d’utilisation. La sécurité de la blockchain est assurée dans cette couche. Dans Bitcoin ou Ethereum, le consensus est atteint grâce à des techniques incitatives appropriées appelées « minage ». Pour qu’une blockchain publique soit autosuffisante, il doit y avoir une sorte de mécanismes d’incitation qui non seulement aide à maintenir le réseau en vie, mais aussi à faire respecter le consensus.

Bitcoin et Ethereum utilisent un mécanisme de consensus Proof of Work (PoW) pour sélectionner au hasard un nœud qui peut proposer un bloc. Une fois que ce bloc est proposé et propagé à tous les nœuds, ils vérifient s’il s’agit d’un bloc valide avec toutes les transactions légitimes et que le processus de PoW a été résolu correctement; ils ajoutent ce bloc à leur propre copie de la blockchain. Il existe de nombreuses variantes différentes de protocoles consensuels tels que la preuve d’enjeu (PoS), le PoS délégué (dPoS), l’algorithme des généraux byzantins (PBFT), etc., que nous aborderons en détail dans les chapitres suivants.

Pourquoi la Blockchain est-elle importante ?

Nous avons examiné les aspects de conception des systèmes centralisés et décentralisés et nous avons eu une idée des avantages techniques des systèmes décentralisés par rapport aux systèmes centralisés.

Nous avons également appris sur les différentes couches de blockchain. Blockchain, étant un système peer-to-peer décentralisé, présentant certains avantages et complexités inhérents. Gardez à l’esprit que ce n’est pas une solution miracle qui peut résoudre tous les problèmes dans le monde, mais il y a des cas spécifiques où il est une solution nécessaire. Il existe également des scénarios où la blockchainisation de la solution existante la rend plus robuste, transparente et sécurisée. Cependant, il peut aussi bien conduire à la catastrophe si elle n’est pas faite de la bonne façon ! Gardons maintenant une perspective commerciale et fonctionnelle à l’esprit et analysons la blockchain.

Limitations des systèmes centralisés

Si vous jetez un coup d’œil rapide au paysage de l’évolution logicielle, vous verrez que de nombreuses solutions logicielles ont une conception centralisée. La raison n’est pas seulement parce qu’elles sont faciles à développer et à entretenir, mais parce que nous sommes habitués à une telle conception pour être en mesure de faire confiance au système. Nous avons toujours besoin d’un tiers de confiance qui peut s’assurer que nous ne sommes pas trompés ou victimes d’une escroquerie. Sans relation d’affaires antérieure, il est difficile de commercer avec quelqu’un ou même d’évoluer le partnership. On ne ferait probablement pas affaire avec quelqu’un que l’on n’a jamais connu.

Prenons un exemple pour mieux comprendre. Aujourd’hui, lorsque nous commandons quelque chose d’Amazon, nous nous sentons en sécurité et assurés de la livraison de l’article. Le producteur de l’article est quelqu’un et l’acheteur est quelqu’un d’autre. Alors quel rôle est joué par Amazon ici? Il est là comme un facilitateur fonctionnant comme un intermédiaire de confiance, et aussi pour prendre une certaine part de la transaction. L’acheteur fait confiance au vendeur lorsque la relation de fiducie est effectivement imposée par des tiers de confiance. Ce que propose la blockchain, c’est que, dans l’ère numérique moderne, nous n’avons pas vraiment besoin d’un tiers entre les deux pour imposer la confiance, et la technologie a assez mûri pour la gérer. Dans la blockchain, la confiance est une partie inhérente du réseau par défaut, que nous explorerons davantage dans les chapitres à venir.

Apprenons rapidement quelques inconvénients d’un système centralisé conventionnel :

• Problèmes de confiance
• Question de sécurité
• Question de confidentialité : la confidentialité de la vente de données est compromise
• Facteur de coût et de temps pour les transactions

Voici quelques-uns des avantages des systèmes décentralisés par rapport aux systèmes centralisés :

• Élimination des intermédiaires
• Vérification plus facile et authentique des transactions
• Sécurité accrue avec un coût moindre
• Une plus grande transparence
• Décentralisé et immuable

Adoption Blockchain jusqu’à présent

Blockchain est venu avec Bitcoin, une crypto-monnaie numérique, en 2009 via une simple liste de diffusion. Peu de temps après son lancement, les gens pouvaient réaliser son véritable potentiel au-delà de la crypto-monnaie. Certaines entreprises ont mis au point différentes offres blockchain telles que Ethereum, Hyperledger, etc. Microsoft et IBM ont mis au jour des offres SaaS (Software as a Service) sur leurs plateformes cloud Azure et Bluemix, respectivement. Différentes start-ups ont été formées, et de nombreuses entreprises établies ont pris des initiatives blockchain qui se sont concentrés sur la résolution de certains problèmes d’affaires qui n’ont pas été facilement résolus avant.

Il est trop tard pour simplement dire que la blockchain a un énorme potentiel pour perturber presque toutes les industries d’une manière ou d’une autre ; la révolution a déjà commencé. Elle a eu un impact énorme sur le marché des services financiers. Il est difficile de nommer une banque mondiale ou une entité financière qui n’explore pas la blockchain. Outre le marché financier, des initiatives ont déjà été prises dans des domaines tels que les médias et le divertissement, la négoce de l’énergie, les marchés de prédiction, les chaînes de vente au détail, les systèmes de fidélisation, les assurances, la logistique et les chaînes d’approvisionnement, les dossiers médicaux, ainsi que les applications gouvernementales et militaires.

Au moment d’écrire ces lignes, la situation actuelle est telle que de nombreuses start-ups et entreprises sont en mesure de voir comment un système basé sur la blockchain peut vraiment répondre à certains domaines de la douleur et devenir bénéfique à bien des égards. Cependant, la conception du bon type de solution blockchain est assez difficile. Il y a de très bonnes idées pour un produit ou une solution basé sur la blockchain, mais il est tout aussi difficile de les construire ou de les mettre en œuvre. Il existe des cas d’utilisation qui ne peuvent être construits que sur une blockchain publique.

Concevoir une blockchain auto-durable avec un écosystème minier approprié est difficile, et quand il s’agit de blockchains publiques existantes pour construire des applications non crypto-monnaie il n’y a rien d’autre que Ethereum. Il est difficile de décider si une application blockchain doit être intégrée uniquement dans la couche d’application et utiliser les couches sous-jacentes telles qu’elles sont, ou si l’application doit être construite à partir de zéro. Il y a aussi des défis techniques. Blockchain est encore en train de mûrir, et il peut prendre quelques années de plus pour l’adoption grand public.

A partir d’aujourd’hui, il existe de multiples propositions pour aborder les questions d’évolutivité de la blockchain. Nous allons essayer de construire une solide compréhension de toutes ces perspectives dans tout ce livre. Pour l’instant, voyons quelques-unes des utilisations spécifiques et des cas d’utilisation dans la section suivante.

Les différents cas d’utilisation de la Blockchain

Dans cette section, nous examinerons certaines des initiatives qui sont déjà prises dans des secteurs tels que la finance, l’assurance, les banques, les soins de santé, le gouvernement, les chaînes d’approvisionnement, l’IdO (Internet des objets), et les médias et le divertissement, pour n’en nommer que quelques-uns. Les possibilités sont illimitées, cependant ! Une véritable économie de partage, difficile à réaliser dans les systèmes centralisés, est possible en utilisant la technologie blockchain (par exemple, les versions peer-to-peer d’Uber, AirBNB). Il est également possible de permettre aux citoyens de posséder leur identité (identité numérique auto-souveraine) et de monétiser leurs propres données à l’aide de cette technologie. Pour l’instant, examinons quelques-uns des cas d’utilisation existants.

• Tout type de bien ou d’actif, qu’il soit physique ou numérique, comme les ordinateurs portables, les téléphones mobiles, les diamants, les automobiles, l’immobilier, les enregistrements en e-immatriculation, les fichiers numériques, etc. peut être enregistré sur blockchain. Cela peut permettre à ces transactions d’actifs d’une personne à l’autre, de maintenir le journal des transactions et de vérifier la validité ou les propriétés. En outre, des services de notaire, une preuve d’existence, des régimes d’assurance sur mesure et bien d’autres cas d’utilisation de ce type peuvent être développés.
• De nombreux cas d’utilisation financière sont en cours de développement sur la blockchain tels que les paiements transfrontaliers, le trading d’actions, la fidélisation et le système de récompenses, Know Your Customer (KYC) entre les banques, etc. Initial Coin Offering (ICO) est l’un des cas d’utilisation les plus tendance à ce jour. ICO est le meilleur moyen de crowdsourcing aujourd’hui en utilisant la crypto-monnaie comme actifs numériques. Une pièce dans une ICO peut être considérée comme un stock numérique dans une entreprise, ce qui est très facile à acheter et à échanger.
• Blockchain peut être utilisé pour permettre à “La Sagesse des Foules” de prendre la tête et de façonner les entreprises, les économies et divers autres phénomènes nationaux en utilisant la sagesse collective ! Des prévisions financières et économiques basées sur la sagesse des foules, des marchés de prédiction décentralisés, un vote décentralisé, ainsi que des opérations boursières peuvent être possibles sur la blockchain.
• Le processus de détermination des redevances musicales a toujours été alambiqué. Les services de streaming musical sur Internet ont facilité une plus grande pénétration du marché, mais ont rendu la détermination des redevances plus complexe. Cette préoccupation peut à peu près être abordée par la blockchain en maintenant un registre public d’informations sur la propriété des droits musicaux ainsi que la distribution autorisée de contenu multimédia.
• C’est l’ère de l’IoT, avec des milliards d’appareils IoT partout et une tendance toujours croissante. Tout un tas de marques, de modèles et de protocoles de communication différents font qu’il est difficile d’avoir un système centralisé pour contrôler les appareils et fournir une plate-forme commune d’échange de données. Il s’agit également d’un domaine où la blockchain peut être utilisée pour construire un système peer-to-peer décentralisé pour que les périphériques IoT communiquent entre eux. ADEPT (Autonomous Decentralized Peer-To-Peer Telemetry) est une initiative conjointe d’IBM et de Samsung qui a développé une plate-forme qui utilise des éléments de la conception sous-jacente du Bitcoin pour construire un réseau distribué d’appareils, un IOT décentralisé. ADEPT utilise trois protocoles : BitTorrent pour le partage de fichiers, Ethereum pour les contrats intelligents et TeleHash pour la messagerie peer-to-peer dans la plate-forme. La fondation IOTA est une autre initiative de ce genre.
• Dans les secteurs publics également, la blockchain a pris de l’ampleur. Il y a des cas d’utilisation où la décentralisation technique est nécessaire, mais politiquement devrait être régie par des gouvernements : l’immatriculation des terres, l’immatriculation et la gestion des véhicules, le vote électronique, etc. sont quelques-uns des cas d’utilisation active. Les chaînes d’approvisionnement sont un autre domaine où il y a quelques cas d’utilisation de grande quantité de blockchain. Les chaînes d’approvisionnement ont toujours été sujettes à des différends à travers le monde, car il a toujours été difficile de maintenir la transparence dans ces systèmes.

Résumé

Dans ce chapitre, nous avons couvert l’évolution de la blockchain, l’histoire de celle-ci, ce qu’elle est, les avantages de conception, et pourquoi il est si important avec certains cas d’utilisation.

Dans les années 1990, l’adoption massive d’Internet a changé la façon dont les gens faisaient des affaires. Il a éliminé la friction de la création et de la distribution de l’information. Cela a ouvert la voie à de nouveaux marchés, plus d’opportunités et de possibilités. De même, la blockchain est ici aujourd’hui pour porter l’Internet à un tout nouveau niveau en supprimant les frictions dans trois domaines clés : le contrôle, la confiance et la valeur.

Contrôle: Blockchain a permis la distribution du contrôle en décentralisant le système.

Confiance: Blockchain est un grand livre immuable et résistant à la falsification. Il donne une source unique et partagée de vérité à tous les nœuds, ce qui rend le système sans confiance. Ce que cela signifie, c’est que la confiance n’est plus nécessaire pour traiter avec une personne ou une entité inconnue et est inhérente à la conception.

Valeur: Blockchain permet l’échange de valeur sous n’importe quelle forme. On peut émettre et transférer des actifs sans entités centrales ou intermédiaires.

Dans le chapitre 2, nous allons plonger en profondeur dans les fondamentaux de la blockchain.

CHAPITRE 2 Comment la Blockchain fonctionne

La blockchain est probablement la plus grande invention depuis l’Internet lui-même ! Il s’agit de la technologie la plus prometteuse pour la prochaine génération de systèmes d’interaction via Internet et a reçu une attention considérable de nombreux secteurs de l’industrie ainsi que par le milieu universitaire. Aujourd’hui, de nombreuses organisations ont déjà réalisé qu’elles devaient être prêtes à maintenir leur position sur le marché. Nous avons déjà examiné quelques cas d’utilisation au chapitre 1, mais les possibilités sont illimitées. Bien que la blockchain ne soit pas une solution miracle pour tous les problèmes d’affaires, elle a commencé à avoir un impact sur la plupart des fonctions commerciales et leurs implémentations technologiques.

Pour être en mesure de résoudre certains problèmes d’affaires du monde réel en utilisant la blockchain, nous avons réellement besoin d’une compréhension fine de ce qu’il est et comment il fonctionne. Pour cela, il doit être compris à travers différentes perspectives telles que les points de vue commerciaux, techniques et juridiques. Ce chapitre est un effort pour entrer dans les écrous et les boulons de la technologie blockchain et obtenir une compréhension complète de la façon dont il fonctionne.

Pose de la Fondation Blockchain

Blockchain n’est pas seulement une technologie, il est principalement couplé avec des fonctions d’affaires et des cas d’utilisation. Dans ses implémentations de crypto-monnaie, elle est également liée aux principes économiques. Dans cette section, nous nous concentrerons principalement sur ses aspects techniques. Techniquement, la blockchain est un brillant amalgame des concepts de la cryptographie, de la théorie des jeux et de l’ingénierie informatique, comme le montre la figure 2-1.

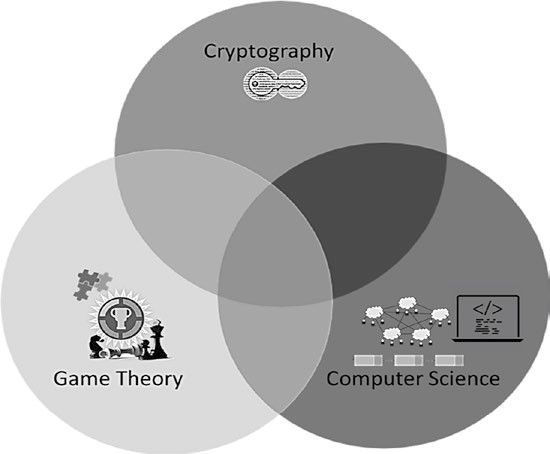
Figure 2-1. La Blockchain au cœur de la blockchain

Jetons un coup d’œil à quel rôle ces composants jouent dans le système de blockchain à un niveau supérieur et approfondissons plus profondément dans les fondamentaux par la suite. Avant cela, revoyons rapidement le fonctionnement des systèmes centralisés traditionnels. L’approche traditionnelle était qu’il y aurait une entité centralisée qui ne conserverait qu’un seul historique de transaction/modification. Il s’agissait d’exercer un contrôle de la concurrence sur l’ensemble de la base de données et d’injecter la confiance dans le système par l’intermédiaire d’intermédiaires. Quel était le problème avec un système aussi stable à l’époque ? Il faut faire confiance à un système centralisé, que les personnes impliquées soient honnêtes ou non ! En outre, le coût dû aux intermédiaires et le temps de transaction pourrait être plus élevé pour des raisons évidentes. Maintenant, pensez à la centralisation du pouvoir ; avoir le plein contrôle de l’ensemble du système permet aux autorités centralisées de faire presque tout ce qu’elles veulent.

Maintenant, regardons comment la blockchain aborde ces questions en raison d’intermédiaires centralisés en utilisant la cryptographie, la théorie des jeux et les concepts informatiques. Indépendamment du cas d’utilisation, les transactions sont sécurisées à l’aide de la cryptographie. En utilisant la cryptographie, on peut s’assurer qu’un utilisateur valide est à l’origine de la transaction et que personne ne peut falsifier une transaction frauduleuse. Cela signifie, cryptographiquement, il peut être assuré que Alice en aucune façon peut faire une transaction au nom de Bob en imitant sa signature.

Maintenant, que faire si un nœud ou un utilisateur tente de lancer une attaque à double dépense (par exemple, on a seulement dix dollars et tente de payer la même chose à plusieurs personnes)? Prêtez une attention particulière ici, bien qu’il n’ait pas suffisamment de fonds, on peut quand même initier une double dépense, ce qui est cryptographiquement correct. La seule façon d’éviter les doubles dépenses est que chaque nœud soit au courant de toutes les transactions. Maintenant, cela conduit à un autre problème intéressant. Étant donné que chaque nœud devrait maintenir la base de données des transactions, comment peuvent-ils tous s’entendre sur un état commun de base de données ?

Encore une fois, comment le système peut-il rester à l’abri des situations où un ou plusieurs nœuds informatiques tentent délibérément de renverser le système et d’essayer d’injecter un état de base de données frauduleux ? La majorité de ces problèmes relèvent du problème des généraux byzantins (décrit plus loin). Eh bien, il a gagné encore plus de popularité en raison de la blockchain, mais il a été là pendant des siècles. Si vous regardez les solutions de centre de données, ou les solutions de base de données distribuées, le problème des généraux byzantins est un problème évident et commun qu’elles traitent pour rester tolérantes aux défauts.

De telles situations et leur solution proviennent en fait de la théorie des jeux. Le domaine de la théorie des jeux fournit une approche radicalement différente pour déterminer comment un système se comportera. Les techniques de la théorie des jeux sont sans doute les plus sophistiquées et réalistes. Ils ne considèrent généralement jamais si un nœud est honnête, malveillant, éthique, ou à d’autres caractéristiques de ce genre et croient que les participants agissent en fonction de l’avantage qu’ils obtiennent, et non par des valeurs morales. Le seul but de la théorie des jeux dans la blockchain est de s’assurer que le système est stable (on parle de l’équilibre de Nash) avec un consensus parmi les participants.

Il existe différents types de problèmes et de situations d’affaires avec des degrés variables de complexités. Ainsi, les protocoles de consensus crypto et théoriciens du jeu sous-jacents pourraient être différents dans différents cas d’utilisation. Toutefois, le principe général de la maintenance d’un journal ou d’une base de données cohérente des transactions vérifiées est le même. Bien que les concepts de cryptographie et la théorie des jeux ont été autour depuis un certain temps maintenant, c’est la pièce d’informatique qui coud ces bits et pièces ensemble grâce à des structures de données et de la technique de communication réseau peer-to-peer. De toute évidence, c’est l’ingénierie logicielle intelligente qui est nécessaire pour réaliser tous les concepts logiques ou mathématiques dans le monde numérique. Ce sont ensuite les techniques d’ingénierie informatique qui intègrent la cryptographie et les concepts théorétiques du jeu dans une application, permettant l’informatique décentralisée et distribuée entre les nœuds avec la structure des données et les composants de communication réseau.

Cryptographie

La cryptographie est la composante la plus importante de la blockchain. Il s’agit certainement d’un domaine de recherche en soi et est basé sur des techniques mathématiques avancées qui sont assez complexes à comprendre. Nous allons essayer de développer une solide compréhension de certains des concepts cryptographiques dans cette section, parce que différents problèmes peuvent nécessiter des solutions cryptographiques différentes ; un type ne convient jamais à tous. Vous pouvez sauter certains détails ou vous y référer au besoin, mais c’est l’élément le plus important pour assurer la sécurité dans le système. Il y a eu de nombreux hacks signalés sur les portefeuilles et les échanges en raison de la conception trop faible ou de mauvaises implémentations cryptographiques.

La cryptographie existe depuis plus de deux mille ans maintenant. C’est la science de garder les choses confidentielles en utilisant des techniques de cryptage. Cependant, la confidentialité n’est pas le seul objectif. Il existe divers autres usages de la cryptographie comme mentionné dans la liste suivante, que nous explorerons plus tard :

• Confidentialité : Seul le destinataire prévu ou autorisé peut comprendre le message. On peut aussi parler de vie privée ou de secret.
• Intégrité des données : Les données ne peuvent pas être falsifiées ou modifiées par un adversaire intentionnellement ou par des erreurs involontaires ou accidentelles. Bien que l’intégrité des données ne puisse pas empêcher la modification des données, elle peut fournir un moyen de détecter si les données ont été modifiées.
• Authentification : L’authenticité de l’expéditeur est assurée et vérifiable par le récepteur.
• Non-répudiation : L’expéditeur, après avoir envoyé un message, ne peut pas nier plus tard qu’ils ont envoyé le message. Cela signifie qu’une entité (une personne ou un système) ne peut pas refuser la propriété d’un engagement antérieur ou d’une action.

Toute information sous la forme d’un message texte, de données numériques ou d’un programme informatique peut être appelée texte clair. L’idée est de chiffrer le texte clair à l’aide d’un algorithme de cryptage et d’une clé qui produit le texte chiffré. Le chiffrement peut ensuite être transmis au destinataire prévu, qui le décrypte à l’aide de l’algorithme de décryptage et de la clé pour obtenir le texte clair.

Prenons un exemple. Alice veut envoyer un message (m) à Bob. Si elle envoie le message tel quel, n’importe quel ennemi, par exemple, Eve peut facilement intercepter le message et la confidentialité est compromise. Ainsi, Alice veut chiffrer le message à l’aide d’un algorithme de cryptage (E) et une clé secrète (k) pour produire le message crypté appelé “chiffretexte”. Un adversaire doit être conscient à la fois de l’algorithme (E) et de la clé(k) pour intercepter le message. Plus l’algorithme et la clé sont forts, plus il est difficile pour l’adversaire d’attaquer. Notez qu’il serait toujours souhaitable de concevoir des systèmes blockchain qui sont au moins prouvablement sécurisés. Ce que cela signifie, c’est qu’un système doit résister à certains types d’attaques réalisables par des ennemis.

L’ensemble commun des étapes de cette approche peut être représenté comme le montre la figure 2-2.

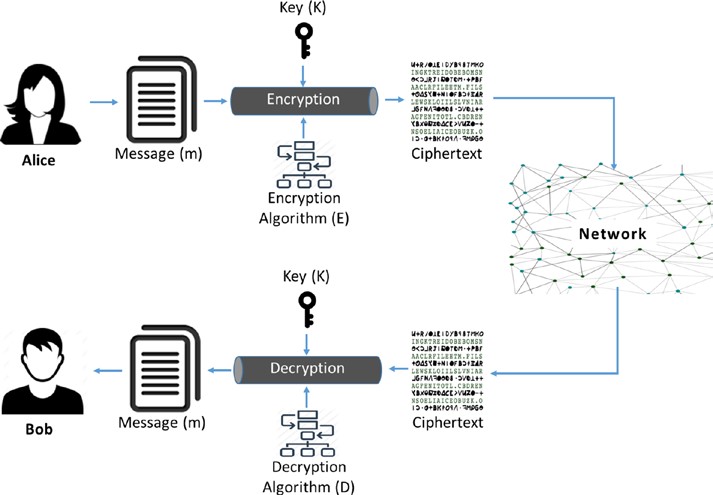
Figure 2-2. Fonctionnement général de la cryptographie

Dans l’ensemble, il existe deux types de cryptographie : la cryptographie de la clé symétrique et la clé asymétrique (alias clé publique). Examinons ces questions individuellement dans les sections suivantes.

Cryptographie symétrique de clé

Dans la section précédente, nous avons examiné comment Alice peut chiffrer un message et envoyer le chiffrement texte à Bob. Bob peut alors déchiffrer le chiffrement texte pour obtenir le message original. Si la même clé est utilisée à la fois pour le chiffrement et le décryptage, elle est appelée cryptographie de clé symétrique. Cela signifie qu’Alice et Bob doivent s’entendre sur une clé (k) appelée « secret partagé » avant d’échanger le chiffrement texte. Ainsi, le processus est le suivant :

Alice—l’expéditeur :

• Chiffrer le message en texte clair m à l’aide de l’algorithme de cryptage E et k clé pour préparer le chiffrement c
• c = E(k, m)
• Envoyer le chiffre texte c à Bob

Bob—le récepteur :

• Décrypter le chiffrement c à l’aide de l’algorithme de décryptage D et de la même clé k pour obtenir le texte clair m
• m = D( k, c )

Avez-vous juste remarqué que l’expéditeur et le récepteur ont utilisé la même clé (k) ? Comment s’entendent-ils sur la même clé et la partagent-elles entre elles ? De toute évidence, ils ont besoin d’un canal de distribution sécurisé pour partager la clé. Il semble généralement comme indiqué dans la figure 2-3.

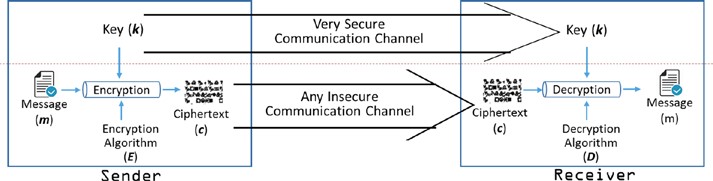
Figure 2-3. Cryptographie symétrique

La cryptographie de clé symétrique est employée couramment ; les utilisations les plus courantes sont les protocoles de transfert de fichiers sécurisés tels que HTTPS, SFTP et WebDAVS. Les crypto systèmes symétriques sont généralement plus rapides et plus utiles lorsque la taille des données est énorme.

Veuillez noter que la cryptographie de clé symétrique existe en deux variantes : les chiffrements de flux et les chiffrements de bloc. Nous en discuterons dans les sections suivantes, mais nous examinerons le principe et la fonction XOR de Kerchoff avant cela pour être en mesure de comprendre comment les crypto systèmes fonctionnent vraiment.

Principe et fonction XOR de Kerckhoff

Le principe de Kerckhoff stipule qu’un crypto système doit être sécurisé même si tout ce qui concerne le système est connu du public, à l’exception de la clé. En outre, l’hypothèse générale est que le canal de transmission de message n’est jamais sécurisé, et les messages pourraient facilement être interceptés pendant la transmission. Cela signifie que même si l’algorithme de cryptage E et l’algorithme de décryptage D sont publics, et qu’il y a une chance que le message puisse être intercepté pendant la transmission, le message est toujours sécurisé en raison d’un secret partagé. Ainsi, les clés doivent être gardées secrètes dans un crypto système symétrique.

La fonction XOR est le bloc de base pour de nombreux algorithmes de cryptage et de décryptage. Jetons un coup d’œil à elle pour comprendre comment il permet la cryptographie. Le XOR, autrement connu sous le nom de « Ou Exclusif» ( en anglais « Exclusive OR ») et dénoté par le symbole ,peut être représenté par le tableau de vérité suivant (tableau 2-1). Il s’agit de la logique Booléenne très utilisée en électronique et en informatique.

Tableau 2-1. Table de Vérité XOR

A	B	A ⊕ B
0	0	0
1	0	1
0	1	1
1	1	0

La fonction XOR a les propriétés suivantes, qui sont importantes pour comprendre les mathématiques derrière la cryptographie :

• Associative : A ⊕ (B ⊕ C) = (A ⊕ B) ⊕ C
• Commutative : A ⊕ B = B ⊕ A
• Négation : A ⊕ 1 = Ā
• Identité : A ⊕ A = 0

En utilisant ces propriétés, il serait maintenant logique de savoir comment calculer le chiffrement texte “c” en utilisant le texte simple “m“ et la clé “k“, puis décrypter le chiffrement texte “c” avec la même clé “k” pour obtenir le texte clair “m. ” La même fonction XOR est utilisée à la fois pour le chiffrement et le décryptage.

m ⊕ k = c et c ⊕ k = m

L’exemple précédent est dans sa forme la plus simple pour comprendre les notions de cryptage et de décryptage. Notez qu’il est très simple d’obtenir le message original en texte clair juste par XORing avec la clé, qui est un secret partagé et seulement connu par les parties visées. Tout le monde peut savoir que l’algorithme de cryptage ou de décryptage ici est XOR, mais pas la clé.

Chiffrement de flux vs chiffrement de bloc

Les algorithmes de chiffrement de flux et de chiffrement de bloc diffèrent dans la façon dont le texte clair est codé et décodé.

Les chiffrements de flux convertissent un symbole de texte clair en un symbole de chiffrement texte. Cela signifie que le chiffrement a effectué un bit ou un octet de texte clair à la fois. Dans un scénario de cryptage petit à petit, pour chiffrer chaque bit de texte clair, une clé différente est générée et utilisée. Ainsi, il utilise un flux infini de bits pseudo random comme la clé et effectue l’opération XOR avec des bits d’entrée de texte clair pour générer du chiffrement text. Pour qu’un tel système reste sécurisé, le générateur de flux de clés pseudo random doit être sécurisé et imprévisible. Les chiffrements de flux sont une approximation d’un chiffrement parfait éprouvé appelé « le bloc-notes unique », dont nous discuterons dans un peu de temps.

Comment le flux de clés pseudo random est-il généré en premier lieu ? Ils sont généralement générés en série à partir d’une valeur de démarrage aléatoire à l’aide de registres numériques de décalage. Les chiffrements de flux sont assez simples et plus rapides dans l’exécution. On peut générer des bits pseudo-aléatoires et décrypter très rapidement, mais cela nécessite une synchronisation dans la plupart des cas.

Nous avons vu que le générateur de nombres pseudo-aléatoires qui génère le flux clé est la pièce centrale ici qui assure la qualité de la sécurité, qui se présente pour être son plus grand inconvénient. Le générateur de nombres pseudo-aléatoires a été attaqué à plusieurs reprises dans le passé, ce qui a conduit à la dépréciation des chiffrements de flux. Le chiffrement de flux le plus largement utilisé est RC4 (Rivest Cipher 4) pour divers protocoles tels que SSL, TLS, et Wi-Fi WEP/WPA etc. Il a été révélé qu’il y avait des vulnérabilités dans RC4, et il a été recommandé par Mozilla et Microsoft de ne pas l’utiliser dans la mesure du possible.

Un autre inconvénient est que toutes les informations contenues dans un bit de texte d’entrée est contenu dans son correspondant de bit de texte chiffré, ce qui provoque un problème de faible diffusion. Il aurait pu être plus sécurisé si l’information d’un bit a été distribuée sur de nombreux bits dans la sortie de chiffrement texte, ce qui est le cas avec les chiffrements de bloc. Des exemples de chiffrements de flux sont un pad unique, RC4, FISH, SNOW, SEAL, A5/1, etc.

Le chiffrement de bloc d’autre part est basé sur l’idée de partitionner le texte clair en blocs relativement plus grands de groupes de bits de longueur fixe, et d’encoder davantage chacun des blocs séparément en utilisant la même clé. Il s’agit d’un algorithme déterministe avec une transformation invariable à l’aide de la clé symétrique. Cela signifie que lorsque vous chiffrez le même bloc de texte clair avec la même clé, vous obtiendrez le même résultat.

Les tailles habituelles de chaque bloc sont 64 bits, 128 bits, et 256 bits appelés longueur de bloc, et leurs blocs de chiffrement texte résultant sont également de la même longueur de bloc. Nous sélectionnons, disons, un r bits clé k pour chiffrer chaque bloc de longueur n, puis remarquez ici que nous avons limité les permutations de la clé k à un sous-ensemble très petit de 2^r. Cela signifie que la notion de « chiffrement parfait » ne s’applique pas. Pourtant, la sélection aléatoire de la clé secrète r bits est importante, dans le sens que plus elle est aléatoire plus le chiffrement est secret.

Pour chiffrer ou déchiffrer un message dans la cryptographie de chiffrement de bloc, nous devons les mettre dans un « mode de fonctionnement » qui définit comment appliquer l’opération d’un chiffrement à un seul bloc à plusieurs reprises pour transformer des quantités de données plus grandes qu’un bloc. Eh bien, le mode de fonctionnement n’est pas seulement de diviser les données en blocs de taille fixe, il a un but plus grand. Nous avons appris que le chiffrement du bloc est un algorithme déterministe. Cela signifie que les blocs avec les mêmes données, lorsqu’ils sont cryptés à l’aide de la même clé, produiront le même chiffrement texte- assez dangereux ! Il fuit beaucoup d’informations. L’idée ici est de mélanger les blocs de plaintext avec les blocs de chiffrement texte juste créé d’une certaine manière de sorte que pour les mêmes blocs d’entrée, leurs sorties correspondantes chiffrées sont différentes. Cela deviendra plus clair lorsque nous arriverons aux algorithmes DES et AES dans les sections suivantes.

Notez que différents modes d’opérations se traduisent par différentes propriétés qui ajoutent à la sécurité du chiffrement de bloc sous-jacent. Bien que nous n’entrerons pas dans la cuisine des modes d’opérations, voici les noms de quelques-uns pour votre culture personnelle: Electronic Codebook (ECB), Cipher Block Chaining (CBC), Cipher Feedback (CFB), Output Feedback (OFB), et Counter (CTR).

Les chiffrements de bloc sont un peu lents à chiffrer ou déchiffrer, comparés aux chiffrements de flux. Contrairement aux chiffrements de flux où la propagation des erreurs est bien moindre, ici l’erreur en un seul bit pourrait corrompre l’ensemble du bloc. Au contraire, les chiffrements de bloc ont l’avantage de la diffusion élevée, ce qui signifie que chaque bit de texte clair d’entré est diffusé à travers plusieurs symboles de chiffrement texte. Des exemples de chiffrements de bloc sont DES, 3DES, AES, etc.

Le déterminisme : Un algorithme déterministe est un algorithme qui, compte tenu d’une entrée particulière, produira toujours la même sortie. (Connu à l’avance, déterminé à l’avance)

Conclusion

	Chiffrement de flux	Chiffrement de blocs
Avantages	Vitesse de transposition Propagation à faible erreur	Diffusion Informations du texte en clair si elles sont diffusées en plusieurs symboles de texte chiffré Un bloc de texte chiffré peut dépendre de plusieurs lettres en texte brut Immunité aux insertions : intégrité Il est impossible d’insérer un seul symbole dans un bloc, La longueur du bloc serait alors incorrecte, et le déchiffrement révélerait rapidement l’insertion, L’intercepteur actif ne peut pas simplement supprimer une lettre de texte chiffré d’un message et en coller une nouvelle pour modifier un compte, une heure, une date ou le nom d’un message
Inconvénients	Diffusion faible (soumis aux outils tels que la distribution de fréquence, la digram analyse, l’indice de coïncidence et la méthode Kasiski Susceptibilité aux insertions et modifications malveillantes (intégrité des données)	Les forces du chiffrement de flux Vitesse Propagation d’erreur

Pad unique (one-time pad)

Il s’agit d’un chiffrement de flux symétrique où le texte clair, la clé et le texte chiffré sont tous des chaînes de bits. En outre, il est entièrement basé sur l’hypothèse d’une clé “purement aléatoire” (et non pseudo aléatoire), en utilisant laquelle il pourrait atteindre le “secret parfait.” En outre, selon la conception, la clé ne peut être utilisée qu’une seule fois. Le problème avec ceci est que la clé devrait être au moins aussi longue que le texte clair. Cela signifie que si vous cryptez un fichier 1 Go, la clé serait également 1 Go! Cela devient impraticable dans de nombreux cas réels.

Exemple:

Tableau 2-2. Exemple de chiffrement à l’aide de la fonction XOR

Clair	1	0	0	1	1	1	0	0	1	0	1	0	1	1	0	1	1	0
Clé	0	1	0	0	1	1	0	1	1	1	0	0	1	0	1	0	1	1
Ciphertext	1	1	0	1	0	0	0	1	0	1	1	0	0	1	1	1	0	1

Vous pouvez vous référer à la table de vérité XOR dans la section précédente pour trouver comment le texte chiffré est généré par XOR-ing plaintext avec la clé. Notez que le texte clair, la clé et le texte chiffré sont tous 18 bits de long.

Ici, le récepteur à la réception du chiffrement peut tout simplement XOR à nouveau avec la clé et obtenir le texte clair. Vous pouvez l’essayer vous-même avec le tableau 2-2 et vous obtiendrez le même texte.

Le principal problème avec ce one-time pad est plus la pratique, plutôt que la théorie. Comment l’expéditeur et le récepteur s’entendent-ils sur une clé secrète qu’ils peuvent utiliser ? Si l’expéditeur et le récepteur ont déjà un canal sécurisé, pourquoi ont-ils même besoin d’une clé ? S’ils n’ont pas de canal sécurisé (c’est pourquoi nous utilisons la cryptographie), alors comment peuvent-ils partager la clé en toute sécurité ? C’est ce qu’on appelle le « problème clé de distribution ».

La solution consiste à approximer le bloc-notes unique à l’aide d’un générateur de nombres pseudo-aléatoires (PRNG). Il s’agit d’un algorithme déterministe qui utilise une valeur source pour générer une séquence de nombres aléatoires qui ne sont pas vraiment aléatoires ; c’est en soi un problème. L’expéditeur et le récepteur doivent avoir la même valeur de démarrage pour que ce système fonctionne. Partager cette valeur source est beaucoup mieux par rapport au partage de la clé entière ; il doit juste être sécurisé. Il est susceptible d’être compromis par quelqu’un qui connaît l’algorithme ainsi que la source.

Norme de chiffrement des données (DES° : Data Encryption Standard)

La norme de chiffrement des données (DES) est une technique de chiffrement de bloc symétrique. Il utilise la taille du bloc 64 bits avec une clé 64 bits pour le chiffrement et le décryptage. Sur la clé 64 bits, 8 bits sont réservés aux contrôles de parité et techniquement 56 bits est la longueur de la clé. Il a été prouvé qu’il est vulnérable aux attaques par brute force et qu’il pourrait être brisé en moins d’un jour. Compte tenu de la loi de Moore, il pourrait être brisé beaucoup plus rapidement à l’avenir, de sorte que son utilisation a été dépréciée un peu en raison de la longueur de la clé. Il était très populaire et était utilisé dans les applications bancaires, les guichets automatiques, et d’autres applications commerciales, et plus encore dans les implémentations matérielles que les logiciels. Nous donnons une description détaillée du chiffrement DES dans cette section.

Dans la cryptographie symétrique, un grand nombre de chiffrements de bloc utilisent un schéma de conception connu sous le nom de « chiffrement de Feistel » ou « réseau Feistel ». Un chiffrement Feistel se compose de plusieurs tours pour traiter le texte clair avec la clé, et chaque tour se compose d’une étape de substitution suivie d’une étape de permutation. Plus le nombre de tours est élevé, plus il est sûr, mais le chiffrement/décryptage ralentit. Le DES est basé sur un chiffrage Feistel de 16 tours.

Une séquence générale d’étapes dans l’algorithme DES est montrée dans la figure 2-4.

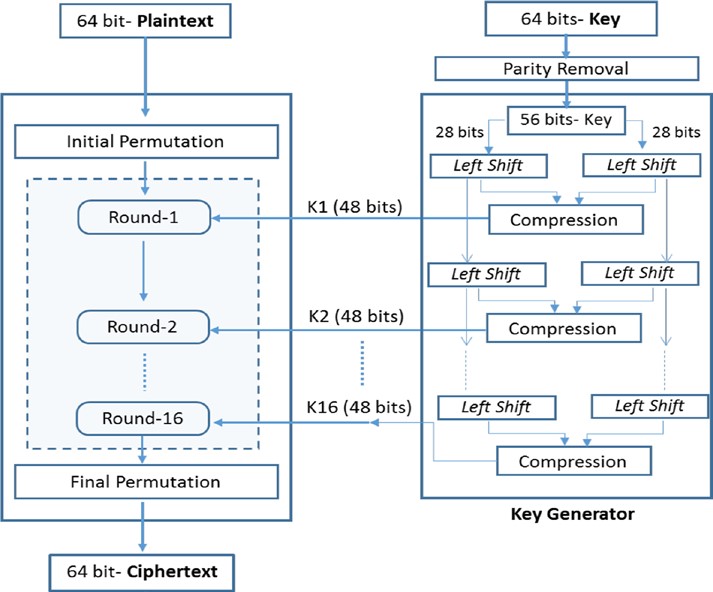
Figure 2-4. Cryptographie DES

Parlons d’abord du générateur de clés, puis nous entrerons dans la partie cryptage.

• Comme mentionné précédemment, la clé est également 64 bits de long. Étant donné que 8 bits sont utilisés comme bits de parité (plus précisément, bit numéro 8, 16, 24, 32, 40, 48, 56 et 64), seulement 56 bits sont utilisés pour le chiffrement et le décryptage.
• Après la suppression de la parité, la clé 56 bits est divisée en deux blocs, chacun de 28 bits. Ils sont alors peu-sage gauche décalée à chaque tour. Nous savons que le DES utilise 16 tours du réseau Feistel. Notez ici que chaque tour prend le bloc de bits décalé à gauche du tour précédent, puis à nouveau à gauche des décalages d’un bit dans le tour actuel.
• Les deux blocs 28 bits décalés à gauche sont ensuite combinés par un mécanisme de compression qui produit une clé de 48 bits appelée sous-clé qui est utilisée pour le chiffrement. De même, à chaque tour, les deux blocs de 28 bits de la ronde précédente se déplacer à nouveau d’un bit, puis matraqué et comprimé à la clé 48 bits. Cette clé est ensuite alimentée à la fonction de cryptage du même tour.

Examinons maintenant comment DES utilise les tours de chiffrement Feistel pour le cryptage:

• Tout d’abord, l’entrée en texte clair est divisée en blocs de 64 bits. Si le nombre de bits dans le message n’est pas également divisible par 64, alors le dernier bloc est rembourré pour en faire un bloc 64 bits.
• Chaque bloc de données d’entrée 64 bits passe par un premier tour de permutation (IP). Il permute simplement, c’est-à-dire, réarrange toutes les entrées 64 bits dans un modèle spécifique en transposant les blocs d’entrée. Il n’a aucune signification cryptographique en tant que telle, et son objectif est de le rendre plus facile à charger le texte clair/chiffretexte dans les puces DE dans le format byte-classé.
• Après le tour IP, le bloc 64 bits est divisé en deux blocs 32 bits, un bloc gauche (L) et un bloc droit (R). Dans chaque tour, les blocs sont représentés comme L_i et R_i, où le sous-scripte “I” désigne le tour. Ainsi, les résultats du cycle d’IP sont désignés comme L₀ et R₀.
• Maintenant, les tours Feistel commencent. Le premier tour prend L₀ et R₀ comme entrée et suit les étapes suivantes:
• Le bloc 32 bits du côté droit (R) vient comme c’est sur le côté gauche et le bloc 32 bits du côté gauche (L) passe par une opération avec le k clé de ce tour et le côté droit du bloc 32 bits (R) comme indiqué ci-dessous:
• L_i et R_et 1
• R_i = L_i – 1 ⊕ F(R_i -1, K_i) où “i” est le nombre du cycle
• Le F() est appelé la “Fonction Decipher” qui est en fait la partie centrale de chaque tour. Il y a plusieurs étapes ou opérations qui sont regroupées dans cette opération F().
• Dans la première étape, le fonctionnement du bloc R 32 bits est élargi et permuté pour produire un bloc de 48 bits.
• Dans la deuxième étape, ce bloc 48 bits est alors XORed avec la sous-clé 48 bits fourni par le générateur de clé de la même ronde.
• Dans la troisième étape, cette sortie XORed 48 bits est alimentée à la boîte de substitution pour réduire les bits de retour à 32 bits. L’opération de substitution dans cette boîte S est la seule opération non linéaire dans DES et contribue de manière significative à la sécurité de cet algorithme.
• Dans la quatrième étape, la sortie 32 bits de la boîte S est alimentée à la boîte de permutation (Boîte P), qui est juste une opération de permutation qui produit un bloc 32 bits, qui est en fait la sortie finale de F() fonction de chiffrement.
• La sortie de F() est alors XORed avec le 32 bits L-block, qui est entrée à ce tour. Cette sortie XORed devient alors la sortie finale de R-block de ce cycle.
• Reportez-vous à la figure 2-5 pour comprendre les diverses opérations qui ont lieu à chaque ronde.

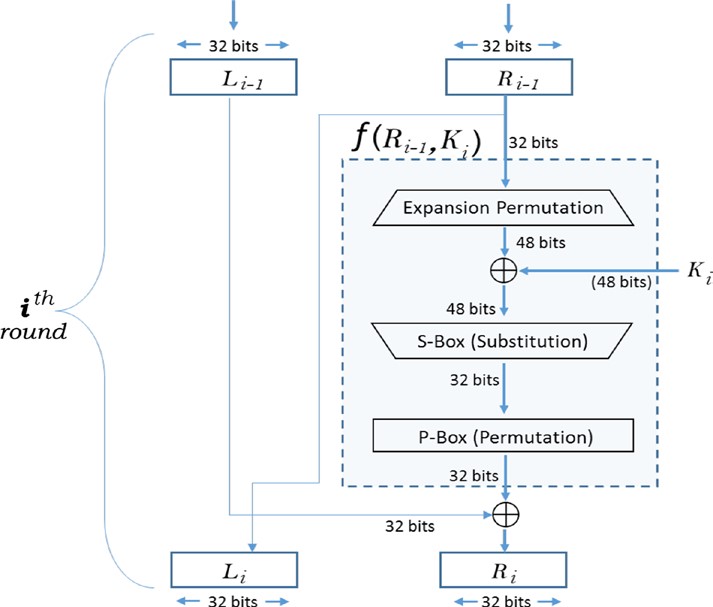
Figure 2-5. Fonction cycle de DES

• Le cycle Feistel précédemment discuté est répété 16 fois, où la sortie d’un tour est alimentée comme entrée à la ronde suivante.
• Une fois que tous les 16 tours sont terminés, la sortie du 16ème tour est à nouveau échangée de telle sorte que la gauche devient le bloc droit et vice versa.
• Ensuite, les deux blocs sont matraqués pour faire un bloc 64 bits et passé par une opération de permutation, qui est l’inverse de la fonction de permutation initiale et qui se traduit par la sortie de texte chiffré 64 bits.

Nous avons examiné comment fonctionne vraiment l’algorithme DES. Le décryptage fonctionne également de la même manière dans l’ordre inverse. Nous n’entrerons pas dans ces détails, mais nous vous laisserons le reste à la découverte.

Concluons avec les limites du DES. La longueur de clé de 56 bits était susceptible à l’attaque de force brute et les S-boxes utilisés pour la substitution dans chaque tour étaient également sujettes à l’attaque de cryptanalyses en raison de quelques faiblesses inhérentes. Pour ces raisons, la norme de chiffrement avancée (AES) a remplacé le DES dans la mesure du possible. De nombreuses applications choisissent maintenant AES plutôt que DES.

Norme de chiffrement avancée (AES : Advances Encryption Standard))

Comme DES, l’algorithme AES est également un chiffrement de bloc symétrique mais n’est pas basé sur un réseau Feistel. L’AES utilise un réseau de substitution-permutation dans un sens plus général. Il offre non seulement une plus grande sécurité, mais offre également une plus grande vitesse ! Selon les normes AES, la taille du bloc est fixée à 128 bits et permet un choix de trois clés : 128 bits, 192 bits, et 256 bits. Selon le choix de la clé, AES est nommé AES-128, AES-192 et AES-256.

Dans AES, le nombre de tours de chiffrement dépend de la longueur de la clé. Pour AES-128, il y a dix tours ; pour AES-192, il y a 12 tours ; et pour AES-256, il y a 14 tours. Dans cette section, notre discussion se limite à la longueur clé 128 (c.-à-d., AES-128), car le processus est presque le même pour d’autres variantes de l’AES. La seule chose qui change, c’est le « calendrier clé », que nous examinerons plus loin dans cette section.

Contrairement à DES, les cycles de cryptage AES sont des itérations et actionnent un bloc de données entier de 128 bits à chaque tour. En outre, contrairement à DES, le décryptage n’est pas très similaire au processus de cryptage dans AES.

Pour comprendre les étapes de traitement dans chaque tour, considérez le bloc 128bit comme 16 octets où les octets individuels sont disposés dans une matrice de 4 à 4 comme indiqué :

Cette matrice de 4 à 4 octets telle qu’indiquée est appelée tableau d’état. Veuillez noter que chaque tour consomme un tableau d’état d’entrée et produit un tableau d’état de sortie.

L’AES utilise également un autre morceau de jargon appelé « mot » qui doit être défini avant d’aller plus loin. Alors qu’un octet se compose de huit bits, un mot se compose de quatre octets, c’est-à-dire de 32 bits. Les quatre octets dans chaque colonne du tableau d’état forment des mots 32 bits et peuvent être appelés mots d’état. Le tableau d’état peut être affiché comme suit :

En outre, chaque octet peut être représenté avec deux nombres hexadécimal.

Exemple : si l’octet 8 bits est {00111010}, il pourrait être représenté comme « 3A » dans la notation Hexadécimale “3” représente les quatre bits gauche “0011” et “A” représente les quatre bits droits “1010”.

Maintenant, pour généraliser chaque tour, le traitement dans chaque tour se produit au niveau octet et se compose de substitution au niveau octet suivie d’une permutation au niveau du mot, d’où il s’agit d’un réseau de substitution-permutation. Nous aurons plus de détails lorsque nous discuterons des différentes opérations de chaque cycle. Le processus global de cryptage et de décryptage de l’AES peut être représenté à la figure 2-6.

Figure 2-6. Cryptographie AES

Si vous avez prêté une attention particulière à la figure 2-6, vous avez remarqué que le processus de décryptage n’est pas seulement le contraire du chiffrement. Les opérations dans les tours sont exécutées dans un ordre différent ! Toutes les étapes de la fonction ronde — SubBytes, ShiftRows, MixColumns, AddRoundKey — sont inversibles. Aussi, notez que les tours sont de nature itérative. La première ronde à la neuvième ronde comporte les quatre opérations, et le dernier tour exclut uniquement l’opération “MixColumns”. Construisons maintenant une compréhension de haut niveau de chaque opération qui se déroule dans une fonction ronde.

SubBytes: Il s’agit d’une étape de substitution. Ici, chaque octet est représenté comme deux chiffres hexadécimaux. À titre d’exemple, prenez un octet {00111010} représenté avec deux chiffres hexadécimaux, par exemple 3A. Pour trouver ses valeurs de substitution, consultez la table de recherche S-box (16 à 16 tables) pour trouver la valeur correspondante pour 3-row et A-column. Ainsi, pour 3A, la valeur substituée correspondante serait {80}. Cette étape fournit la non-linéarité dans le chiffrement.

ShiftRows: Il s’agit de l’étape de transformation et est basée sur la représentation de la matrice du tableau de l’état. Il se compose des opérations de quart suivantes :

• Aucun déplacement circulaire de la première rangée, et reste tel quel
• Déplacement circulaire de la deuxième rangée par un octet vers la gauche
• Déplacement circulaire de la troisième rangée par deux octets vers la gauche
• Déplacement circulaire de la quatrième rangée (dernière rangée) par trois octets vers la gauche

Il peut être représenté comme indiqué :

MixColumns: C’est aussi une étape de transformation où les quatre colonnes de l’Etat se multiplient avec un polynomial fixe (C_x) et se transforment en nouvelles colonnes. Dans ce processus, chaque octet d’une colonne est cartographié à une nouvelle valeur qui est une fonction des quatre octets dans la colonne. Ceci est réalisé par la multiplication de la matrice de l’état comme indiqué :

La multiplication de matrice est comme d’habitude, mais les produits ET sont XORed. Voyons l’un des exemples pour comprendre le processus. Byte 0′ est calculé comme indiqué :

Byte 0′ = (2 . Byte0) ⊕ (3 . Byte1) ⊕ Byte3 ⊕ Byte4

Il est important de noter que cette étape MixColumns, avec l’étape ShiftRows, fournit la propriété de diffusion nécessaire (information d’un octet est diffusé à plusieurs octets) au chiffrement.

AddRoundKey: Il s’agit à nouveau d’une étape de transformation où la clé ronde 128bit est au niveau du bit XORed avec 128 bits d’état dans un ordre de colonne majeure. Ainsi, l’opération a lieu au niveau de la colonne, ce qui signifie quatre octets d’une colonne d’état de mot avec un mot de la clé ronde. De la même manière que nous avons représenté le bloc de texte clair 128 bits, la clé 128 bits devrait également être représentée dans la même matrice 4 à 4 comme indiqué ici :

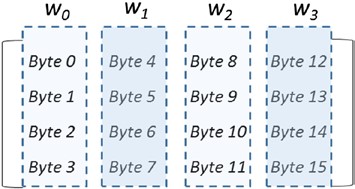
Clé 128 bits

Cette opération affecte chaque bit d’un état. Maintenant, se rappeler qu’il y a dix tours, et chaque tour a sa propre clé ronde. Étant donné qu’il y a une étape “AddRoundKey” avant le début des tours, il y a en fait onze (10+1) opérations AddRoundKey. Dans un tour, tous les 128 bits de sous-clé, c’est-à-dire les quatre mots de sous-clé, sont utilisés pour XOR avec le bloc de données d’entrée 128 bits. Donc, au total, nous avons besoin de 44 mots clés, w₀ à w₄₃. C’est pourquoi la clé 128 bits doit passer par une opération d’expansion clé, que nous allons obtenir dans un peu de temps.

Notez ici que le mot clé [w₀, w₁, w₂, w₃] obtient XORed avec le bloc d’entrée initial avant le traitement à base de rond commence. Les 40 touches de mots restantes, w₄ à w₄₃, utilisent quatre mots à la fois dans chacun des dix tours.

AES Key Expansion: L’algorithme d’extension de la clé AES prend comme entrée une clé de chiffrement de 128 bits (clé de quatre mots) et produit un calendrier de 44 mots clés à partir de celui-ci. L’idée est de concevoir ce système de telle sorte qu’un changement d’un bit dans la clé affecterait de manière significative toutes les clés rondes.

L’opération d’expansion clé est conçue de telle sorte que chaque groupement d’une clé de quatre mots produit le groupement suivant d’une clé de quatre mots dans une base de quatre à quatre mots. Il est facile d’expliquer cela avec une représentation picturale, alors nous y voilà:

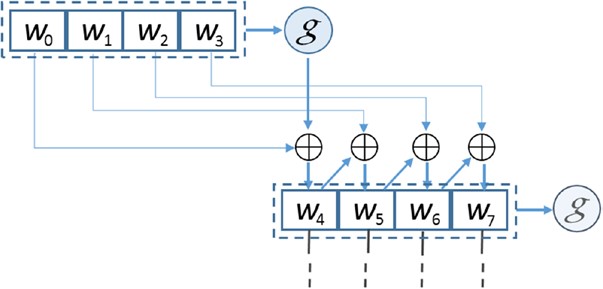
Figure 2-7. Expansion clé d’AES

Nous allons rapidement passer en revue les opérations qui ont lieu pour la clé d’expansion en se référant au diagramme :

• La touche initiale de 128 bits est [w₀, w₁, w₂, w₃] arrangé en quatremots.
• Jetez un oeil au mot élargi maintenant : [w₄, w₅, w₆, w₇]. Notez que w₅ dépend de w₄ et w₁. Cela signifie que chaque mot élargi dépend du mot immédiatement précédent, c’est-à-dire, w_i – 1 et le mot qui est de quatre positions en arrière, c’est-à-dire, w_i – 4 . Testez la même chose pour w₆ . Comme vous pouvez le voir, juste une simple opération XOR est effectuée ici.
• Maintenant, qu’en est-il de w_4? Ou, toute autre position qui est un multiple de quatre, comme w₈ ou w_12? Pour ces mots, une fonction plus complexe dénotée comme «g» est utilisée. Il s’agit essentiellement d’une fonction en trois étapes. Dans la première étape, le bloc d’entrée de quatre mots passe par le décalage circulaire gauche par un octet. Par exemple [w₀, w₁, w₂, w₃] devient[w₁, w₂, w₃, w₀]. Dans la deuxième étape, le mot d’entrée des quatre octets (par exemple, [w₁, w₂, w₃, w₀]) est pris comme entrée et la substitutionoctet est appliquée sur chaque octet à l’aide de S-box. Puis, dans la troisième étape, le résultat de l’étape 2 est XORed avec quelque chose appelé rond constante dénoté comme Rcon[ ]. La constante ronde est un mot dans lequel les trois octets les plus à droite sont toujours nuls. Par exemple, [x, 0, 0, 0]. Cela signifie que le but de Rcon[ ] est de simplement effectuer XOR sur l’octet le plus à gauche de l’étape 2 mot clé de sortie. Notez également que le Rcon[ ] est différent pour chaque tour. De cette façon, la sortie finale de la fonction complexe “g” est générée, qui est alors XORed avec w_i 4 pour obtenir w_i où “i” est un multiple de 4.
• C’est ainsi que se déroule la mise en place de la clé d’expansion dans l’AES.

Le tableau d’état de sortie du dernier tour est réarrangé pour former le bloc de chiffrement de 128 bits. De même, le processus de décryptage se déroule dans un ordre différent, que nous avons examiné dans le diagramme du processus AES. L’idée était de vous donner un point de vu général sur la façon dont cet algorithme fonctionne à un niveau élevé, et nous allons limiter notre discussion à seulement le processus de cryptage dans cette section.

L’algorithme AES est standardisé par le NIST (National Institute of Standards and Technology). Il avait la limitation du long temps de traitement. Supposons que vous envoyez seulement un fichier de 1 mégaoctet (8388608 bits) en cryptant avec AES. À l’aide d’un algorithme AES de 128 bits, le nombre d’étapes requises pour ce chiffrement sera de 8388608/128 à 65536 sur ce même nombre de blocs de données ! En utilisant une approche de traitement parallèle, l’efficacité AES peut être augmentée, mais n’est toujours pas très approprié lorsque vous avez affaire à de grands volumes de données.

Défis dans la cryptographie des clés symétriques

Il y a quelques limites dans la cryptographie symétrique de clé. Quelques-uns d’entre eux sont énumérés comme suit :

• La clé doit être partagée par l’expéditeur et le récepteur avant toute communication. Il faut mettre en place un mécanisme d’établissement de clé sécurisé.
• L’expéditeur et le récepteur doivent se faire confiance, car ils utilisent la même clé symétrique. Si un récepteur est piraté par un attaquant ou que le récepteur a délibérément partagé la clé avec quelqu’un d’autre, le système est compromis.
• Un vaste réseau de n nœuds, par exemple, nécessitent n(n-1)/2 paires de clés à gérer.
• Il est conseillé de continuer à changer la clé pour chaque séance de communication.
• Souvent, un tiers de confiance est nécessaire pour une gestion efficace des clés, ce qui est lui-même un gros problème.

Fonctions de hachage cryptographiques

Les fonctions de hachage sont les fonctions mathématiques qui sont les primitives cryptographiques les plus importantes et font partie intégrante de la structure des données de la blockchain. Ils sont largement utilisés dans de nombreux protocoles cryptographiques, applications de sécurité de l’information telles que les signatures numériques et les codes d’authentification des messages (MACs : Message Authentification Codes). Puisqu’ils sont employés dans la cryptographie asymétrique de clés, nous en discuterons ici avant d’entrer dans la cryptographie asymétrique. Veuillez noter que les concepts abordés dans cette section peuvent ne pas être conformes aux manuels académiques, et un peu biaisés vers l’écosystème de la blockchain.

Les fonctions de hachage cryptographique sont une classe spéciale de fonctions de hachage qui sont aptes à la cryptographie, et nous limiterons notre discussion en se rapportant à elle seulement. Ainsi, une fonction de hachage cryptographique est une fonction à sens unique qui convertit les données d’entrée de longueur arbitraire et produit une sortie de longueur fixe. La sortie est généralement appelée «hash value » ou « message digest». Il peut être représenté comme indiqué Figure 2-8.

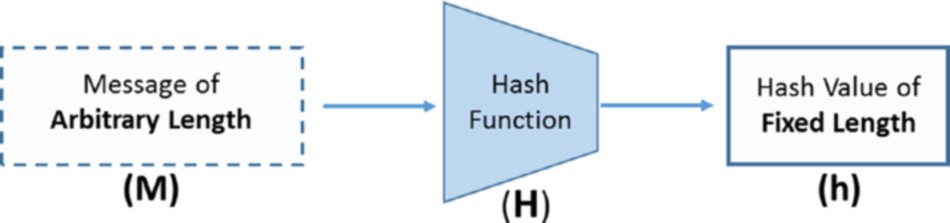
Figure 2-8. Fonction de hachage dans sa forme basique

Pour que les fonctions de hachage servent leur but de conception et soient utilisables, elles devraient avoir les propriétés de noyau suivantes :

• L’entrée peut être n’importe quelle chaîne de n’importe quelle taille, mais la sortie est de longueur fixe, par exemple, une sortie de 256 bits ou une sortie de 512 bits à titre d’exemples.
• La valeur de hachage doit être efficacement calculable pour n’importe quel message donné.
• Il est déterministe, en ce sens que la même entrée lorsqu’elle est fournie à la même fonction de hh produit la même valeur de hheth à chaque fois.
• Il est infaisable (mais pas impossible !) d’inverser et de générer le message à partir de sa valeur de hachage, sauf en essayant de tous les messages possibles.
• Tous les petits changements dans le message devraient grandement influencer le hachage de sortie, juste pour que personne ne puisse corréler la nouvelle valeur de hachage avec l’ancienne après un petit changement.

En dehors des propriétés de base mentionnées ci-dessus, ils doivent également répondre aux propriétés de sécurité suivantes pour être considéré comme un protocole cryptographique:

• Résistance aux collisions : Cela implique qu’il est impossible de trouver deux entrées différentes, par exemple, X et Y, qui hachent à la même valeur.

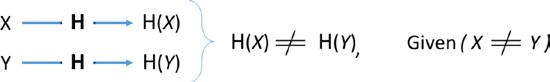
Cela rend la fonction hash H() résistante aux collisions parce que personne ne peut trouver X et Y, de même que H(X) H(Y). Notez que cette fonction de hachage est une fonction de compression, car elle comprime une entrée donnée à la sortie de taille fixe qui est plus courte que l’entrée. Ainsi, l’espace d’entrée est trop grand (n’importe quoi de n’importe quelle taille) comparé à l’espace de sortie, qui est fixe. Si la sortie est une valeur de hachages de 256 bits, alors l’espace de sortie peut avoir un maximum de 2²⁵⁶ valeurs, et pas au-delà. Cela implique qu’une collision doit exister. Cependant, il est extrêmement difficile de trouver cette collision. Selon la théorie du « paradoxe d’anniversaire », nous pouvons en déduire qu’il devrait être possible de trouver une collision en utilisant la racine carrée de l’espace de sortie. Donc, en prenant 2¹²⁸ + 1entrées, il est très probable de trouver une collision ; mais c’est un nombre extrêmement énorme à calculer, ce qui est tout à fait infaisable!

Discutons maintenant où cette propriété pourrait être utile. Dans la majorité du stockage en ligne, du stockage de fichiers en nuage, du stockage blob, des App Stores, etc., la propriété « résistance aux collisions » est largement utilisée pour assurer l’intégrité des fichiers. Exemple : quelqu’un calcule le « message digest » d’un fichier et les télécharge sur le stockage en nuage. Plus tard, quand ils téléchargent le fichier, ils pourraient simplement calculer le digest message à nouveau et recouper avec l’ancien. De cette façon, il peut être assuré si le fichier a été corrompu en raison de certains problèmes de transmission ou peut-être en raison de certaines tentatives délibérées. C’est en raison de la résistance à la collision que personne ne peut arriver à un fichier différent ou un fichier modifié qui serait haché à la même valeur que celle du fichier d’origine.

• Résistance préimage : Cette propriété signifie qu’il est informatiquement impossible d’inverser une fonction de hachage; c’est-à-dire qu’il est impossible de trouver l’entrée X de la sortie H(X). Par conséquent, cette propriété peut également être appelée propriété «cachée». Faites très attention ici; il y a un autre aspect subtil à cette situation. Notez que lorsque X peut être n’importe quoi dans le monde, cette propriété est facilement atteinte. Cependant, s’il n’y a qu’un nombre limité de valeurs que X peut prendre, et qui est connu de l’adversaire, ils peuvent facilement calculer toutes les valeurs possibles de X et trouver lequel on hache au résultat.

Exemple : Un laboratoire a décidé de préparer le message pour le résultat réussi d’une expérience afin que tout adversaire qui a accès à la base de données des résultats ne puisse pas comprendre le sens parce que ce qui est stocké dans le système sont des sorties hachées. Supposons qu’il ne peut y avoir que trois résultats possibles de l’expérience comme OP111, OP112, et OP113, dont un seul est réussi, par exemple, OP112. Ainsi, le laboratoire décide de le hacher, calculer H(OP112), et stocker les valeurs hachées dans le système. Bien qu’un adversaire ne puisse pas trouver OP112 de H(OP112), il peut simplement déjouer tous les résultats possibles de l’expérience, c’est-à-dire H(OP111), H(OP112) et H(OP113) et voir que seul H(OP112) correspond à ce qui est stocké dans le système. Une telle situation est certainement vulnérable ! Cela signifie que, lorsque l’entrée à une fonction de hachage provenant d’un espace limité et ne provient pas d’une distribution étalée, elle est faible. Cependant, il y a une solution à ce sujet comme suit :

Prenons une entrée, disons “X” qui n’est pas très étalée, tout comme les résultats de l’expérience dont nous venons de discuter avec quelques valeurs possibles. Si nous pouvons concaténer que avec une autre entrée aléatoire, disons « r », qui vient d’une distribution de probabilité avec une entropie min élevé, alors il sera difficile de trouver X de H(r X). Ici, l’entropie élevée de min signifie que la distribution est très étalée et qu’il n’y a aucune valeur particulière qui est susceptible de se produire. Supposons que “r” a été choisi à partir de la distribution 256bit. Pour un adversaire d’obtenir la valeur exacte de “r” qui a été utilisé avec l’entrée, il y a une probabilité de succès de 1/2²⁵⁶, qui est presque impossible à atteindre. La seule façon est de considérer toutes les valeurs possibles de cette distribution une par une, ce qui est encore une fois pratiquement impossible. La valeur “r” est également appelée “nonce”. En cryptographie, un nonce est un nombre aléatoire qui ne peut être utilisé qu’une seule fois.

Discutons maintenant où cette propriété de la résistance préimage pourrait être utile. Il est très utile pour s’engager à une valeur, de sorte que « engagement » est le cas d’utilisation ici. Cela peut être mieux expliqué avec un exemple. Supposons que vous avez participé à une sorte de paris ou de jeu événement. Disons que vous devez vous engager à votre option, et le déclarer ainsi. Cependant, personne ne devrait être en mesure de comprendre ce que vous pariez, et vous-même ne pouvait pas nier plus tard sur ce que vous pariez. Ainsi, vous tirez parti de la propriété de résistance préimage de la fonction de hachage. Vous prenez un hach du choix sur qui vous pariez, et le déclarer publiquement. Personne ne peut inverser la fonction de hachage et comprendre ce que vous pariez. En outre, vous ne pouvez pas dire plus tard que votre choix était différent, parce que si vous hachez un choix différent, il ne pourra pas correspondre à ce que vous avez déclaré publiquement. Il est conseillé d’utiliser un nonce “r” comme nous l’avons expliqué dans le paragraphe précédent pour concevoir de tels systèmes.

Deuxième résistance préimage : Cette propriété est légèrement différente de la « résistance aux collisions ». Il implique que, compte tenu d’une entrée X et de son hach H(X), il est impossible de trouver Y, de sorte que H(X) = H(Y). Contrairement à la propriété résistante aux collisions, ici la discussion est pour un X donné, qui est fixé. Cela implique que si une fonction de hachage est déjà résistante à la collision, alors elle est résistante à la deuxième préimage aussi.

Il y a une autre propriété dérivée des propriétés mentionnées qui est très utile dans Bitcoin. Examinons-le d’un point de vue technique et apprenons comment Bitcoin l’exploite pour l’exploitation minière lorsque nous atteindrons le chapitre 3. Le nom de cette propriété est “puzzle convivialité”, “puzzle friendliness.” Ce nom implique qu’il n’y a pas de raccourci vers la solution et la seule façon d’arriver à la solution est de traverser toutes les options possibles dans l’espace d’entrée. Nous n’essaierons pas de le définir ici, mais nous essaierons directement de comprendre ce que cela signifie vraiment.

Considérons cet exemple : H(r || X) = Z, où “r” est choisi à partir d’une distribution avec une haute entropie min, “X” est l’entrée concaténée avec “r “, et “Z” est la valeur de sortie hachée. La propriété signifie qu’il est beaucoup trop difficile pour un adversaire de trouver une valeur “Y” qui hachent exactement à “Z“. C’est-à-dire, H(r || Y) = Z, où r est une partie de l’entrée choisie de la même manière aléatoire que “r.” Ce que cela signifie, c’est que, lorsqu’une partie de l’entrée est substantiellement aléatoire, il est difficile de briser la fonction de hachage avec une solution rapide ; la seule façon est de tester avec toutes les valeurs aléatoires possibles.

Dans l’exemple précédent, si “Z” est une sortie n-bits, alors il n’a pris qu’une valeur sur 2ⁿ valeurs possibles. Notez soigneusement qu’une partie de votre entrée, disons «r», provient d’une distribution élevée d’entropie min, qui doit être jointe avec votre entrée X. Maintenant vient la partie intéressante de la conception d’un puzzle de recherche. Disons que Z est une sortie n-bits et est un ensemble de 2ⁿ valeurs possibles, pas seulement une valeur exacte. On vous demande de trouver une valeur de r telle que lorsqu’il est haché en jointure à X, il tombe dans cet ensemble de sortie de 2ⁿ valeurs; puis il forme un puzzle de recherche. L’idée est de trouver toutes les valeurs possibles de r jusqu’à ce qu’il tombe avec la gamme de Z. Notez ici que la taille de Z a limité l’espace de sortie à un plus petit ensemble de 2ⁿ valeurs possibles. Plus l’espace de sortie est petit, plus le problème est difficile. Évidemment, si la gamme est grande, il est plus facile de trouver une valeur en elle et si la gamme est assez étroite avec seulement quelques possibilités, alors trouver une valeur dans cette gamme est difficile. C’est la beauté du “r“, appelée “nonce” dans l’entrée à la fonction de hachage. Quelle que soit la valeur aléatoire de r que vous prendrez, il sera concaténé avec “X” et passera par la même fonction de hachage, encore et encore, jusqu’à ce que vous obtenez la bonne valeur nonce “r” qui satisfait la gamme requise pour Z, et il n’y a absolument aucun raccourci à elle, sauf pour essayer toutes les valeurs possibles!

Notez que pour une sortie de valeur de hachage de n-bit, un effort moyen de 2ⁿ est nécessaire pour briser la résistance préimage et la seconde préimage, et de 2ⁿ/2 pour la résistance aux collisions.

Nous avons discuté de diverses propriétés fondamentales et de sécurité des fonctions de hachage. Dans les sections suivantes, nous verrons quelques fonctions de hachage importantes et nous rentrerons plus profondément dans l’application.

Un heads-up sur différentes fonctions de haussier

L’une des fonctions de hachage ou de compression les plus anciennes est la fonction de hachage MD4. Elle appartient à la famille de message digest (MD). D’autres membres de la famille MD sont MD5 et MD6, et il existe de nombreuses autres variantes de MD4 comme RIPEMD. Les familles d’algorithmes MD produisent un message digest de 128 bits en consommant des blocs de 512 bits. Ils ont été largement utilisés comme checksums pour vérifier l’intégrité des données. De nombreux serveurs de fichiers ou référentiels logiciels utilisés pour fournir un checksum MD5 pré-computé, que les utilisateurs pouvaient vérifier par rapport au fichier qu’ils ont téléchargé. Cependant, il y avait beaucoup de vulnérabilités trouvées dans la famille MD et il a été déprécié.

Une autre de ces familles de fonctions de hachage est l’algorithme de hachage sécurisé. Il y a essentiellement quatre algorithmes dans cette famille, tels que SHA-0, SHA-1, SHA-2, et SHA- 3. Le premier algorithme proposé dans cette famille a été nommé SHA, mais les versions plus récentes étaient à venir avec des correctifs de sécurité et des mises à jour, de sorte qu’un rétronyme a été appliqué à elle et il a été fait SHA0. Il a été constaté qu’il avait une faille de sécurité grave mais non divulguée et a été abandonnée. Plus tard, SHA-1 a été proposé en remplacement de SHA-0.

SHA-1 avait une étape de calcul supplémentaire qui a abordé le problème dansSHA-0. Les deux SHA-0 et SHA-1 étaient des fonctions de hachage de 160 bits qui ont consommé des blocs de taille de 512 bits. SHA-1 a été conçu par la National Security Agency (NSA) pour l’utiliser dans l’algorithme de signature numérique (DSA). Il a été utilisé beaucoup dans de nombreux outils de sécurité et des protocoles Internet tels que SSL, SSH, TSL, etc. Il a également été utilisé dans les systèmes de contrôle de version tels que Mercurial, Git, etc pour les contrôles de cohérence, et pas vraiment pour la sécurité. Plus tard, vers 2005, des faiblesses cryptographiques y ont été trouvées et elles ont été dépréciées après l’année 2010. Nous allons comprendre SHA-2 et SHA-3 en détail dans les sections suivantes.

SHA-2

Il appartient à la famille SHA des fonctions de hachage, mais lui-même est une famille de fonctions de hachage. Il a de nombreuses variantes SHA telles que SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224, et SHA-512/256. SHA-256 et SHA-512 sont les fonctions primitives de hachage et les autres variantes en sont dérivées. La famille SHA-2 de fonctions de hachage sont largement utilisés dans des applications telles que SSL, SSH, TSL, PGP, MIME, etc. très connues et utilisées en informatique.

SHA-224 est une version tronquée de SHA-256 avec une valeur initiale différente ou un vecteur d’initialisation (IV). Notez que les variantes SHA avec différentes troncatures appliquées peuvent produire les mêmes sorties de hachage de taille en bit, d’où différents vecteurs d’initialisation sont appliqués dans différentes variantes SHA pour être en mesure de les différencier correctement.

Pour en revenir au calcul SHA-224, il s’agit d’un processus en deux étapes. Tout d’abord, la valeur SHA-256 est calculée avec un IV différent par rapport à la valeur par défaut utilisée dans SHA-256. Deuxièmement, la valeur de hachage de 256 bits qui en résulte est une troncature à 224 bits ; généralement les 224 bits de gauche sont conservés, mais le choix est à définir en fonction des préférences.

SHA-384 est une troncature de SHA-512, juste la façon dont SHA-224 est une version tronquée de SHA-256. De même, les versions 512/224 et SHA-512/256 sont des versions tronquées de SHA-512.

Vous vous demandez pourquoi ce concept de « troncature » existe? Notez que la troncation n’est pas seulement limitée à ceux que nous venons de mentionner, et il peut y avoir diverses autres variantes ainsi. Les principales raisons de la troncation pourraient être les suivantes :

• Certaines applications nécessitent un message digest avec une certaine longueur qui est différente de celle par défaut.
• Indépendamment de la variante SHA-2 que nous utilisons, nous pouvons sélectionner un niveau de troncature en fonction de la propriété de sécurité que nous voulons maintenir. Exemple : Compte tenu de l’état de puissance de calcul d’aujourd’hui, lorsque la résistance aux collisions est nécessaire, nous devons conserver au moins 160 bits et lorsque seule la pré-résistance à l’image est nécessaire, nous devrions en conserver au moins 80 bits. La propriété de sécurité telle que la résistance aux collisions diminue avec la troncation, mais elle devrait être choisi de telle sorte qu’il serait informatiquement impossible de trouver une collision.
• La troncation aide également à maintenir la compatibilité vers l’arrière avec les applications plus anciennes. Exemple : SHA224 offre une sécurité de 112 bits qui peut correspondre à la longueur de clé du triple-DES (3DES).

Parlant d’efficacité, SHA-256 est basé sur un mot 32 bits et SHA512 est basé sur un mot 64 bits. Ainsi, sur une architecture 64 bits, SHA-512 et toutes ses variantes tronquées peuvent être calculer plus rapidement avec un meilleur niveau de sécurité par rapport à SHA-1 ou d’autres variantes SHA-256.

Le tableau 2-3 est une représentation tabulaire tirée du papier NIST qui représente SHA-1 et différentes propriétés d’algorithmes SHA-2 en un mot.

Tableau 2-3. FONCTION de hachage SHA-1 et SHA-2 en bref

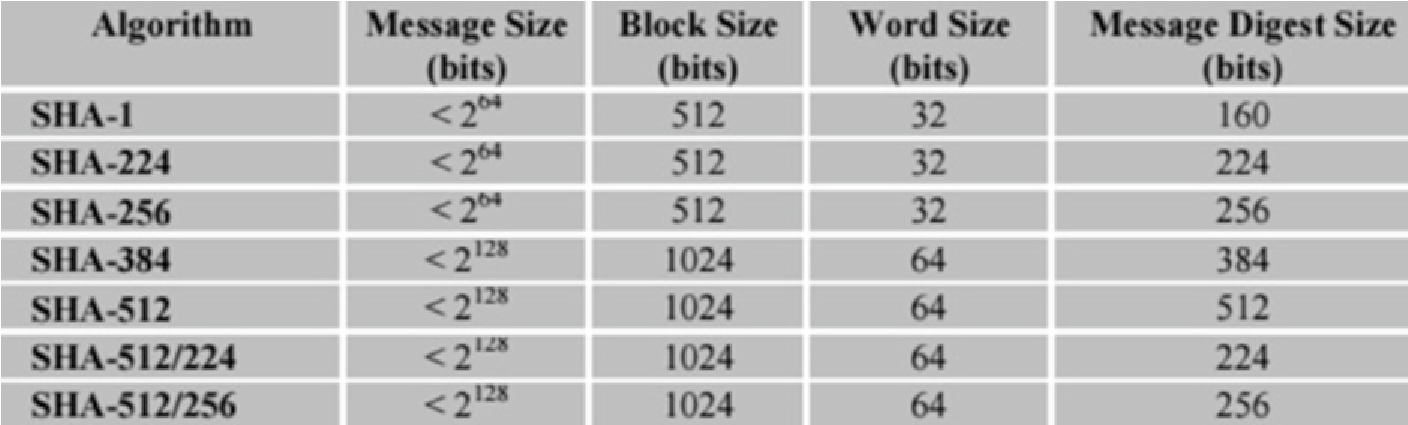
En règle générale, il est conseillé de ne pas tronquer lorsqu’il n’est pas nécessaire. Certaines fonctions de hachage tolèrent la troncation et d’autres non, et cela dépend aussi de la façon dont vous l’utilisez et dans quel contexte.

SHA-256 et SHA-512

Comme mentionné, SHA-256 appartient à la famille SHA-2 des fonctions de hachage, et c’est celui utilisé dans Bitcoins ! Rien que ça, comme son nom l’indique, il produit une valeur de hachage de 256 bits, d’où le nom. Ainsi, il peut fournir 2¹²⁸ bits de sécurité selon le paradoxe d’anniversaire (mentionné plus haut).

Rappelez-vous que les fonctions de hachage prennent une entrée arbitraire de longueur et produisent une sortie de taille fixe. L’entrée de longueur arbitraire n’est pas alimentée comme c’est le cas pour la fonction de compression et est divisée en blocs de longueur fixe avant d’être alimentée à la fonction de compression. Cela signifie qu’une méthode de construction est nécessaire qui peut itérer à travers la fonction de compression en construisant des blocs d’entrée de taille fixe à partir de données d’entrée de longueur arbitraire et de produire une sortie de longueur fixe. Il existe différents types de méthodes de construction telles que la construction de Merkle-Damgard, la construction d’arbres et la construction d’éponges. Il est prouvé que si la fonction de compression sous-jacente est résistante aux collisions, alors la fonction globale de hachage avec n’importe quelle méthode de construction devrait également être résistante à la collision.

La méthode de construction utilisée par SHA-256 est la construction de Merkle-Damgàrd, alors voyons comment elle fonctionne dans la figure 2-9.

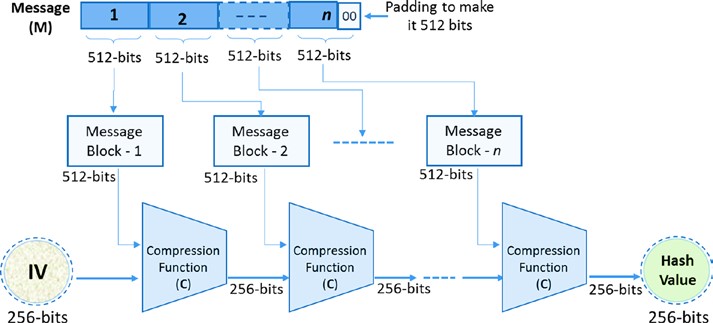
Figure 2-9. Construction de Merkle-Damgàrd pour SHA-256

Se référant au diagramme, les étapes suivantes (présentées à un niveau élevé) sont exécutées dans l’ordre spécifié pour calculer la valeur finale du hashage :

• Comme vous pouvez le voir dans le diagramme, le message est d’abord divisé en blocs de 512 bits. Lorsque le message n’est pas un multiple exact de 512 bits (ce qui est généralement le cas), le dernier bloc est en deçà de bits, d’où il est rembourré pour le faire 512 bits.
• Les blocs de 512 bits sont en outre divisés en 16 blocs de mots 32 bits (16 ‘ 32 ‘512).
• Chaque bloc passe par 64 tours de fonction ronde où chaque mot 32 bits passe par une série d’opérations. Les fonctions rondes sont une combinaison de certaines fonctions communes telles que XOR, ET, OU, NON, décalage au niveau du bit gauche / droite, etc et nous n’entrerons pas dans ces détails dans cet article, mais pourquoi pas dans un prochain article plus complet sur la cryptographie.

Semblable à SHA-256, les étapes et les opérations sont assez similaires dans SHA-512, comme SHA-512 utilise également la construction Merkle-Damgard. La principale différence est qu’il y a 80 tours de fonctions rondes dans SHA-512 et la taille du mot est de 64 bits. La taille du bloc dans SHA-512 est de 1024 bits, qui est encore divisé en 16 blocs de mots 64 bits Le message digest de sortie est de 512 bits de longueur, c’est-à-dire, huit blocs de mots 64 bits. Alors que SHA512 prenait de l’ampleur et commençait à être utilisé dans de nombreuses applications, quelques personnes se sont tournées vers l’algorithme SHA-3 pour être prêtes pour l’avenir. SHA-3 est juste une approche différente de hachage et non pas un véritable remplacement de SHA-256 ou SHA-512, mais il permet l’ajustement. Nous allons apprendre quelques détails supplémentaires sur SHA-3 dans les sections suivantes.

Ripemd

La fonction de hachage RACE Integrity Primitives Evaluation Message Digest (RIPEMD) est une variante de la fonction de hachage MD4 avec presque les mêmes considérations de conception. Comme il est utilisé dans Les Bitcoins, nous aurons une brève discussion à ce sujet.

L’original RIPEMD était de 128 bits, plus tard RIPEMD-160 a été développé. Il existe des versions 128-, 256 et 320 bits de cet algorithme, appelé RIPEMD-128, RIPEMD-256, et RIPEMD-320, respectivement, mais nous limiterons notre discussion à la RIPEMD-160 la plus populaire et la plus largement utilisée.

RIPEMD-160 est une fonction de hachage cryptographique dont la fonction de compression est basée sur la construction de Merkle-Damgàrd. L’entrée est divisée en blocs de 512 bits et le rembourrage est appliqué lorsque les bits d’entrée ne sont pas un multiple de 512. La valeur de hachage est de 160 bits et est généralement représentée en nombres hexadécimale à 40 chiffres.

La fonction de compression est composée de 80 étapes, composées de deux lignes parallèles de cinq tours de 16 étapes chacune (5 x 16 = 80). La fonction de compression fonctionne sur seize mots 32 bits (blocs de 512 bits).

Notez que Bitcoin utilise à la fois le hachage sha-256 et ripeMD-160 ensemble pour la génération d’adresses. ripeMD-160 est utilisé pour raccourcir davantage la production de valeur de sortie de hachage de sha- 256 à 160 bits.

SHA-3 (EN)

En 2015, l’algorithme Keccak (prononcé comme «ket-chak») a été standardisé par le NIST comme le SHA-3. Notez que le but n’était pas vraiment de remplacer la norme SHA-2, mais de compléter et de coexister avec elle, même si l’on peut choisir SHA-3 sur SHA-2 dans certaines situations.

Étant donné que SHA-1 et SHA-2 étaient basés sur la construction de Merkle-Damgàrd, une approche différente de la fonction de hachage était souhaitable. Ainsi, ne pas utiliser la construction de Merkle-Damgard était l’un des critères fixés par le NIST. C’est parce que la nouvelle conception ne devrait pas souffrir des limites de la construction Merkle-Damgard tels que les multi-collisions. Keccak, qui est devenu SHA-3, a utilisé une méthode de construction différente appelée construction d’éponge.

Afin d’assurer la rétrocompatibilité, il était nécessaire que SHA-3 soit en mesure de produire des sorties de longueur variable telles que 224, 256, 384, et 512 bits et aussi d’autres sorties de longueur arbitraires. De cette façon, SHA-3 est devenu une famille de fonctions de hachage cryptographique telles que SHA3-224, SHA3-256, SHA3-384, SHA3 -512, et deux fonctions de sortie extensible (XOFs), appelées SHAKE128 et SHAKE256. En outre, SHA-3 devait avoir un paramètre réglable (capacité) pour permettre un compromis entre la sécurité et la performance. Puisque SHAKE128 et SHAKE256 sont des XOF, leur production peut être étendue à n’importe quelle longueur désirée, d’où le nom.

Le diagramme suivant (figure 2-10) montre comment SHA-3 (algorithme de Keccak) est conçu à un niveau élevé.

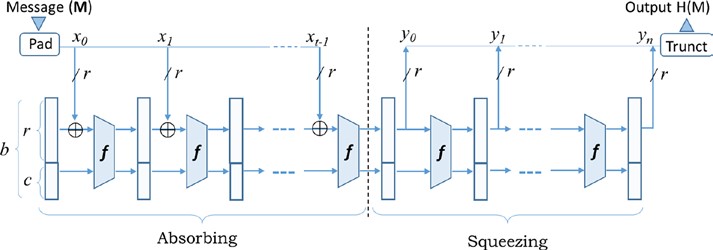
Figure 2-10. Construction d’éponge pour SHA-3

Voici une série d’étapes qui ont lieu pour SHA-3 :

• Comme vous pouvez le voir dans la figure 2-10, le message est d’abord divisé en blocs (x_i)de taille r bits. Si les données d’entrée ne sont pas un multiple de bits r, alors le rembourrage est nécessaire. Si vous vous interrogez sur ce r, ne vous inquiétez pas, nous y arriverons dans un peu de temps. Maintenant, concentrons-nous sur la façon dont ce rembourrage se produit. Pour un bloc de message x_i qui n’est pas un multiple de r et a un certain message m en elle, le rembourrage se passe comme indiqué dans ce qui suit: x_i = m || P 1 {0}* 1

“P” est une chaîne de bits prédéterminée suivie de 1 {0} 1, ce qui signifie un leader et à la traîne 1 et un certain nombre de zéros (pourrait être pas zéro bits aussi) qui peut faire x_i un multiple de r. Le tableau 2-4 montre les différentes valeurs de P.

Tableau 2-4. Rembourrage en variantes SHA-3

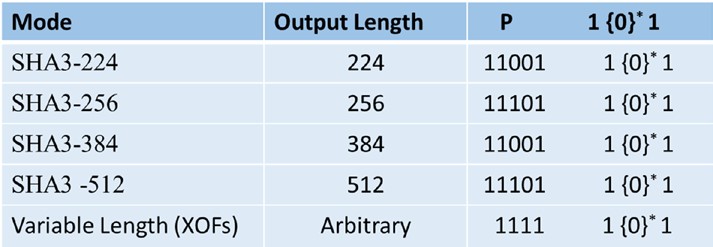
• Comme vous pouvez le voir dans la figure 2-10, il y a généralement deux phases à la construction d’éponges SHA-3 : la première est la phase « Absorbante » pour l’entrée, et la seconde est la phase « Pressante » pour la sortie. Dans la phase absorbante, les blocs de message (x_i) passent par diverses opérations de l’algorithme et dans la phase Pressante, la sortie de longueur configurable est calculée. Notez que pour ces deux phases, la même fonction appelée “Kecaak-f” est utilisée.
• Pour le calcul de SHA3-224, SHA3-256, SHA3384, SHA3 -512, qui est effectivement un remplacement de SHA-2, seuls les premiers bits du premier bloc de sortie y₀ sont utilisés avec le niveau requis de troncation.
• Le SHA-3 est conçu pour être réglable pour sa résistance de sécurité, l’entrée et les tailles de sortie à l’aide des paramètres de tuning.
• Comme vous pouvez le voir dans le diagramme, “b” représente la largeur de l’état et exige que r + c = b. En outre, “b” dépend de l’exposant “l” tels que b = 25 x 2^l
• Étant donné que « l » peut prendre des valeurs comprises entre 0 et 6, « b » peut avoir des largeurs de 25, 50, 100, 200, 400, 800 et 1600. Il est conseillé de ne pas utiliser les deux plus petites valeurs de “b” dans la pratique car ils sont juste là pour analyser et effectuer la cryptanalyse sur l’algorithme.
• Dans l’équation r + c = b, le “r” que nous voyons est ce que nous avons utilisé pour prétraiter le message et divisé en blocs de longueur “r”. C’est ce qu’on appelle le « taux de bits ». En outre, le paramètre “c” est appelé la capacité qui a juste à satisfaire la condition r + c = b ∈ {25, 50, 100, 200, 400, 800, 1600} et obtenir calcul. De cette façon, “r” et “c” sont utilisés comme paramètres de tuning pour faire l’ajustement entre la sécurité et la performance.
• Pour SHA-3, la valeur exposante l est fixée à «6», de sorte que la valeur de b est de 1600 bits. Pour cela étant donné b = 1600, deux valeurs de débit de bits sont permises : r = 1344 et r = 1088. Cela conduit à deux valeurs distinctes de « c ». Donc, pour r = 1344, c = 256 et pour r = 1088, c = 512.
• Examinons maintenant le moteur central de cet algorithme, c’est-à dire keccak-f, qui est également appelé “Keccak-f Permutation.” Il y a des tours “n” dans chaque Keccak-f, où “n” est calculé comme: n = 12 + 2l. Puisque la valeur de l est de 6 pour SHA-3, il y aura 24 tours dans chaque Keccak-f. Chaque tour prend des bits “b” (r + c) entrée et produit le même nombre de bits “b” que la sortie.
• Dans chaque tour, l’entrée “b” est appelée un état. Ce tableau d’état “b” peut être représenté comme un tableau en trois dimensions b = ( 5 x 5 x w), où la taille du mot w = 2^l. Donc, w = 64 bits, ce qui signifie 5 x 5 = 25 mots de 64 bits chacun. Rappelez-vous que l=6 pour SHA-3, donc b = 5 x 5 x 64 = 1600. Le tableau 3D peut être affiché comme dans la figure 2-11.

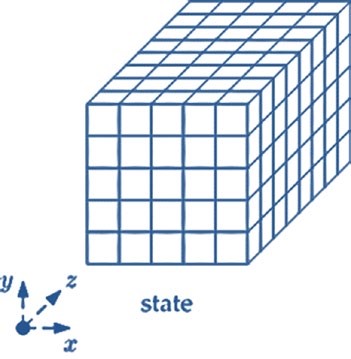
Figure 2-11. Représentation du tableau d’État dans SHA-3

• Chaque tour se compose d’une séquence de cinq étapes et le tableau d’état est manipulé dans chacune de ces étapes comme indiqué dans la figure 2-12.

Figure 2-12. Les cinq étapes de chaque tour SHA-3

• Sans entrer dans les détails de chacune des cinq étapes, apprenons rapidement ce qu’ils font à un niveau élevé :
• Theta() étape: Il effectue l’opération XOR pour fournir une diffusion mineure.
• Rho ()étape: Il effectue une rotation au niveau des bits de chacun des 25 mots.
• Pi() étape: Il effectue la permutation de chacun des 25 mots.
• Chi (-) étape: Dans cette étape, les bits sont remplacés en combinant ceux avec leurs deux bits suivants dans leurs lignes.
• Iota ()étape : Il XOR une constante ronde en un mot d’état pour briser la symétrie.
• Le dernier tour de Keccak-f produit la sortie y_0, ce qui est suffisant pour le mode de remplacement SHA-2, c’est-à-dire, la sortie avec 224, 256, 384, et 512 bits. Notez que les bits les moins significatifs de y₀ sont utilisés pour la sortie de longueur désirée. En cas de sortie de longueur variable, avec y₀, autres bits de sortie de y₁, y₂, y₃… peut également être utilisé.

Quand il s’agit de la mise en œuvre de la vie réelle de SHA-3, il est constaté que ses performances sont bonnes dans le logiciel (mais pas aussi bonnes que SHA-2) et est excellentes dans le matériel (mieux que SHA-2).

Applications des fonctions de haussier

Les fonctions de hachage cryptographique ont de nombreux usages différents dans différentes situations. Voici quelques exemples de cas d’utilisation :

• Les fonctions de hachage sont utilisées pour vérifier l’intégrité et l’authenticité de l’information.
• Les fonctions de hachage peuvent également être utilisées pour indexer les données dans les tables de hachage. Cela peut accélérer le processus de recherche. Au lieu de l’ensemble des données, si nous recherchons en fonction des hachages (en supposant que la valeur de hachage beaucoup plus courte par rapport à l’ensemble des données), alors il devrait évidemment être plus rapide.
• Ils peuvent être utilisés pour authentifier en toute sécurité les utilisateurs sans stocker les mots de passe localement. Imaginez une situation où vous ne voulez pas stocker des mots de passe sur le serveur, évidemment parce que si un adversaire pirate sur le serveur, ils ne peuvent pas obtenir le mot de passe de leurs hachages stockées. Chaque fois qu’un utilisateur tente de se connecter, le hachage du mot de passe poinçonné est calculé et comparé au hachage stocké. Sécurisé, n’est-ce pas ?
• Étant donné que les fonctions de hachage sont des fonctions à sens unique, elles peuvent être utilisées pour implémenter PRNG.
• Bitcoin utilise les fonctions de hachage comme algorithme de preuve de travail (PoW). Nous entrerons dans les détails de celui-ci lorsque nous travaillerons sur le Bitcoin.
• Bitcoin utilise également des fonctions de hachage pour générer des adresses afin d’améliorer la sécurité et la confidentialité.
• Les deux applications les plus importantes sont les signatures numériques et dans les MACs tels que les codes d’authentification des messages à base de hachage (HMACs).

Comprendre le fonctionnement et les propriétés des fonctions de haussier, il peut y avoir divers autres cas d’utilisation où les fonctions de hachage peuvent être utilisés.

L’Internet Engineering Task Force (IETF) a adopté la version 3.0 du protocole SSL (SSLv3) en 1999, rebaptisé en protocole de sécurité de la couche de transport (TLS) version 1.0 (TLSv1) et l’a défini en RFC 2246. SSLv3 et TLSv1 sont compatibles en ce qui concerne les opérations de base.

Exemples de code des fonctions de haussier

Voici quelques exemples de code de différentes fonctions de hachage. Cette section est juste destinée à vous donner une vision sur la façon d’utiliser les fonctions de hachage programmatique. Les exemples de code sont en Python, mais seraient assez similaires dans différentes langues ; vous avez juste à trouver les bonnes fonctions de bibliothèque à utiliser.

# -*- coding: utf-8 -*-

import hashlib

# hashlib est un module populaire pour faire du hachage en python

#Construction des fonctions md5(), sha1(), sha224(), sha256(), sha384() et sha512() presentes dans le module hashlib

md=hashlib.md5()

md.update(“Le renard brun rapide saute par-dessus le chien paresseux”)

print md.digest()

print “Digest Size:”, md.digest_size, “\n”, “Block Size: “,

md.block_size

# Comparaison des différents messages digest de SHA224, SHA256,SHA384,SHA512

print “Digest SHA224”, hashlib.sha224(“Le renard brun rapide saute par-dessus le chien paresseux”).hexdigest()

print “Digest SHA256”, hashlib.sha256(“Le renard brun rapide saute par-dessus le chien paresseux”).hexdigest()

print “Digest SHA384”, hashlib.sha384(“Le renard brun rapide saute par-dessus le chien paresseux”).hexdigest()

print “Digest SHA512”, hashlib.sha512(“Le renard brun rapide saute par-dessus le chien paresseux”).hexdigest()

# Toutes les sorties de hachage sont uniques

# Exemple de hachage avec RIPEMD160 160 bit

h = hashlib.new(‘ripemd160′)

h.update(“Le renard brun rapide saute par-dessus le chien paresseux”)

h.hexdigest()

# Algorithme de dérivation de clé :

# Les algorithmes de hachage natifs ne sont pas résistants aux attaques par bruteforce.

# Des algorithmes de déviation de clé sont utilisés pour sécuriser le hachage de mot de passe.

import hashlib, binascii

algorithm=’sha256′

password=’HomeWifi’

salt=’salt’

# salt est une donnée aléatoire qui peut être utilisée comme une entrée additionnelle sur une fonction unidirectionnelle

nu_rounds=1000

key_length=64

#dklen est la taille de la clé dérivée

dk = hashlib.pbkdf2_hmac(algorithm,password, salt, nu_rounds, dklen=key_length)

print ‘derieved key: ‘,dk

print ‘derieved key in hexadeximal :’, binascii.hexlify(dk)

# Message de vérification des propriétés de hachage

import hashlib

input = “Sample Input Text”

for i in xrange(20):

# ajouter l’itérateur à la fin du texte

input_text = input + str(i)

# afficher le résultat d’entrée et de hachage

print input_text, ‘:’, hashlib.sha256(input_text).

hexdigest()

MAC et HMAC

HMAC est un type de MAC (code d’authentification de message). Comme son nom l’indique, le but d’un MAC est de fournir l’authentification de message en utilisant la clé symétrique et l’intégrité du message en utilisant des fonctions de hachage. Ainsi, l’expéditeur envoie le MAC avec le message pour le récepteur afin de le vérifier et de lui faire confiance. Le récepteur a déjà la clé K (comme la cryptographie de clé symétrique est utilisée, de sorte que l’expéditeur et le récepteur sont déjà en accord sur elle); ils l’utilisent simplement pour calculer le MAC du message et le vérifier par rapport au MAC qui a été envoyé avec le message.

Dans sa forme la plus simple, MAC = H(clé||message). HMAC est en fait une technique pour transformer les fonctions de hachage en MACs. Dans HMAC, les fonctions de hachage peuvent être appliquées plusieurs fois avec la clé et ses clés dérivées. Les HMAC sont largement utilisés dans les systèmes RFID, TLS, etc. Dans SSL/TLS (HTTPS est TTP dans SSL/TLS), HMAC est utilisé pour permettre au client et au serveur de vérifier et de s’assurer que les données échangées n’ont pas été modifiées pendant la transmission. Jetons un coup d’œil à quelques-unes des stratégies importantes de MAC qui sont largement utilisées :

• MAC-then-Encrypt: Cette technique nécessite le calcul du MAC sur le texte clair, l’ajoutant aux données, puis cryptant tout cela ensemble. Ce schéma ne fournit pas l’intégrité du texte chiffré. À la fin de la réception, le décryptage du message doit d’abord se produire pour pouvoir vérifier l’intégrité du message. Il assure toutefois l’intégrité du texte clair. TLS utilise ce schéma de MAC pour s’assurer que la session de communication client-serveur est sécurisée.
• Encrypt-and-MAC: Cette technique nécessite le cryptage et le calcul MAC du message ou du texte clair, puis l’application du MAC à la fin du message crypté ou du chiffrement. Notez que MAC est calculé sur le texte clair, de sorte que l’intégrité du texte clair peut être assurée, mais pas du texte chiffré, ce qui laisse la place à certaines attaques. Contrairement au schéma précédent, l’intégrité du texte clair peut être vérifiée. SSH (Secure Shell) utilise ce système MAC.
• Encrypt-then-MAC: Cette technique exige que le texte clair doit d’abord être crypté, puis calculer le MAC sur le texte chiffré. Ce MAC du texte chiffré est ensuite annexé au chiffrement lui-même. Ce schéma assure l’intégrité du texte chiffré, il est donc possible de vérifier d’abord l’intégrité et, si elle est valide, de le déchiffrer. Il filtre facilement les chiffrages invalides, ce qui le rend efficace dans de nombreux cas. En outre, puisque MAC est en texte chiffré, en aucun cas il ne révèle des informations sur le texte clair. Il est généralement le plus idéal de tous les régimes et a des implémentations plus larges. Il est utilisé dans IPsec.

Cryptographie de clé asymétrique

La cryptographie asymétrique, également connue sous le nom de « cryptographie à clé publique », est un concept révolutionnaire introduit par Diffie et Hellman. Avec cette technique, ils ont résolu le problème de la distribution des clés dans un système de cryptographie symétrique en introduisant des signatures numériques. Notez que la cryptographie asymétrique des clés n’élimine pas le besoin de cryptographie de clé symétrique. Ils se complètent habituellement ; les avantages de l’un peuvent compenser les inconvénients de l’autre.

Voyons un scénario pratique pour comprendre comment un tel système fonctionne. Supposons qu’Alice veut envoyer un message à Bob confidentiellement afin que personne d’autre que Bob ne peut donner un sens au message, alors il faudrait les étapes suivantes :

Alice—L’expéditeur :

• Chiffrer le message en texte clair m à l’aide de l’algorithme de cryptage E et de la clé publique Puk_Bob pour préparer le texte chiffré c.
• c = E (Puk_Bob, m )
• Envoyez le texte chiffré c à Bob.

Bob—Le récepteur :

• Décrypter le texte chiffré c à l’aide de l’algorithme de décryptage D et de sa clé privée Prk_Bob pour obtenir le texte clair d’origine m.
• m = D(Prk_Bob, c)

Un tel système peut être représenté comme indiqué à la figure 2-13.

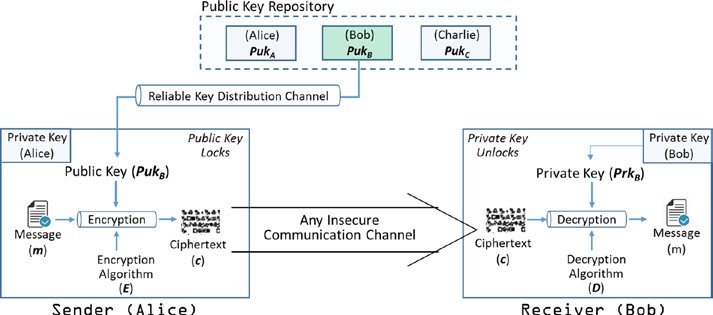
Figure 2-13. Cryptographie asymétrique pour la confidentialité

Notez que la clé publique doit être conservée dans un dépôt public accessible à tous et que la clé privée doit être gardée comme un secret bien gardé. La cryptographie à clé publique offre également un moyen d’authentification. Le récepteur, Bob, peut vérifier l’authenticité de l’origine du message m de la même manière.

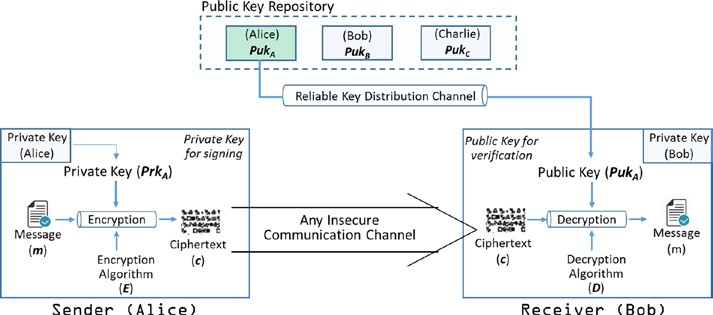
Figure 2-14. Cryptographie asymétrique pour l’authentification

Dans l’exemple de la figure 2-14, le message a été préparé à l’aide de la clé privée d’Alice, de sorte qu’il pourrait être assuré qu’il ne venait que d’Alice. Ainsi, l’ensemble du message a servi de signature numérique. Notez que la confidentialité et l’authentification sont souhaitables. Pour faciliter cela, le chiffrement des clés publiques doit être utilisé deux fois. Le message doit d’abord être crypté avec la clé privée de l’expéditeur pour fournir une signature numérique. Ensuite, il doit être crypté avec la clé publique du récepteur pour fournir la confidentialité. Il peut être représenté comme :

• c = E[Puk_Bob, E(Prk_Alice, m)]
• m = D[Puk_Alice, D(Prk_Bob, c)]

Comme vous pouvez le voir, le décryptage se produit dans juste son ordre inverse. Notez que la cryptographie à clé publique est utilisée quatre fois ici: deux fois pour le chiffrement et deux fois pour le décryptage. Il est également possible que l’expéditeur signe le message en appliquant la clé privée à un petit bloc de données dérivées du message à envoyer, et non à l’ensemble du message. Dans le monde réel, les magasins d’applications tels que Google Play ou Apple App Store exigent que les applications logicielles soient signées numériquement avant d’être publiées.

Nous avons examiné les utilisations des deux clés dans la cryptographie asymétrique, qui peut être résumée comme suit:

• Les clés publiques sont connues et accessibles à tous. Ils peuvent être utilisés pour chiffrer le message ou pour vérifier les signatures.
• Les clés privées sont extrêmement privées pour les particuliers. Ils sont utilisés pour déchiffrer le message ou pour créer des signatures.

Dans la cryptographie à clé asymétrique ou publique, il n’y a pas de problème de clé de distribution, car l’échange de la clé convenue n’est plus nécessaire. Cependant, cette approche représente un défi de taille. Comment s’assurer que la clé publique qu’ils utilisent pour chiffrer le message est vraiment la clé publique du destinataire visé et non d’un intrus ou d’un espion ? Pour résoudre ce problème, la notion d’un tiers de confiance appelé infrastructure à clé publique (ICP) est introduite. Grâce à PKIs, l’authenticité des clés publiques est assurée par le processus d’attestation ou de notarisation de l’identité de l’utilisateur. La façon dont les IK fonctionnent est qu’ils fournissent des clés publiques vérifiées en les incorporant dans un certificat de sécurité en les signant numériquement.

Le système de chiffrement à clé publique peut également être appelé fonction à sens unique ou fonction trappe. C’est parce que le cryptage d’un texte clair en utilisant la clé publique “Puk” est facile, mais l’autre direction est pratiquement impossible. Personne ne peut vraiment déduire le texte clair original du texte chiffré crypté sans connaître la clé secrète ou privée “Prk”, qui est en fait l’information trappe. En outre, dans le contexte des clés, ils sont mathématiquement liés, mais il est par calcul impossible de trouver l’une de l’autre.

Nous avons discuté des objectifs importants de la cryptographie à clé publique tels que l’établissement clé, l’authentification et la non-répudiation par le biais de signatures numériques, et la confidentialité par le cryptage. Cependant, tous les algorithmes de cryptographie à clé publique ne peuvent pas fournir toutes ces trois caractéristiques. En outre, les algorithmes sont différents en termes de leur problème de calcul sous-jacent et sont classés en conséquence. Certains algorithmes tels que RSA sont basés sur le schéma de factorisation intégriste, car il est difficile de factoriser de grands nombres. Certains algorithmes sont basés sur les problèmes discrets de logarithme dans les champs finis tels que l’échange de clés Diffie-Hellman (DH) et DSA. Une version généralisée des problèmes discrets de logarithme est la courbe elliptique (EC) des régimes de clé publique. L’algorithme de signature numérique elliptique de courbe (ECDSA) en est un exemple. Nous couvrirons la plupart de ces algorithmes dans la section suivante.

RSA

L’algorithme RSA, nommé d’après Ron Rivest, Adi Shamir et Leonard Adleman est peut-être l’un des algorithmes cryptographiques les plus utilisés. Il est basé sur la difficulté pratique de la factorisation d’un très grand nombre. Dans RSA, le texte clair et le chiffrement sont des entiers entre 0 et n – 1 pour certains n.

Nous discuterons du régime RSA sous deux aspects. La première est la génération de paires de clés et la deuxième, comment fonctionne le chiffrement et le décryptage. Étant donné que l’arithmétique modulaire fournit le mécanisme pour la génération de clé, regardons rapidement.

Arithmétique modulaire

Soit m un entier positif appelé module. Deux entiers a et b sont modulo m congru si:

a ≡ b (mod m), ce qui implique a – b = m . k pour un entier k.

Exemple : si a ≡ 16 (mod 10) alors a peut avoir les solutions suivantes : a =. . ., -24, -14, -4, 6, 16, 26, 36, 46

L’un de ces nombres soustrait par 16 est divisible par 10. Par exemple, −24 −16 = −40, qui est divisible par 10. Notez qu’a ≡ 36 (mod 10) peut aussi avoir les mêmes solutions de a.

Selon le théorème d’Euclide seule une solution unique de «a» existe qui remplit la condition: 0 ≤ a <m. Dans l’exemple a ≡ 16 (mod 10), seule la valeur 6 satisfait la condition 0 ≤ 6 <10. C’est ce qui sera utilisé dans le processus de chiffrement / déchiffrement de l’algorithme RSA.

Voyons maintenant l’inverse modulaire. Si b est l’inverse d’a modulo m, alors il peut être représenté comme :

a b ≡ 1 (mod m), ce qui implique que a b – 1 = m. k pour un entier k.

Exemple : 3 a l’inverse 7 modulo 10

3 · 7 = 1 (mod 10) => 21 – 1 = 20, qui est divisible par 10.

Génération de paires de clés

Comme nous l’avons déjà vu, une paire de clés privées et publiques est nécessaire pour que toute partie participant à une crypto-communication asymétrique. Dans le régime RSA, la clé publique se compose de (e, n) où n est appelé le module et e est appelé l’exposant public. De même, la clé privée se compose de (d, n), où n est le même module et d est l’exposant privé.

Voyons comment ces clés sont générées avec un exemple :

• Générez une paire de deux grands nombres premiers p et q.

Prenons deux petits nombres premiers comme exemple ici pour faciliter la compréhension. Alors, laissez les deux les nombres premiers soient p = 7 et q = 17.

• Calculez le module RSA (n) comme n = pq. Ce n devrait être un grand nombre, généralement un minimum de 512 bits. Dans notre exemple, le module (n) = pq = 119.
• Trouver un exposant public e tel que 1 < e < (p – 1) (q – 1) et il ne doit pas y avoir de facteur commun pour e et (p – 1) (q – 1) sauf 1. Cela implique que e et (p – 1) (q – 1) sont coprime. Notez qu’il peut y avoir plusieurs valeurs qui remplissent cette condition et peut être considéré comme e, mais n’importe laquelle devrait être prise.
• Dans notre exemple, (p – 1) (q – 1) = 6 × 16 = 96. Donc, e peut être relativement premier et inférieur à 96. Supposons que e soit 5.
• Maintenant, la paire de nombres (e, n) forme la clé publique et devrait être rendu public. Donc, dans notre exemple, la clé publique est (5, 119).
• Calculer l’exposant privé d à l’aide de p, q et e considérant que le nombre d est l’inverse de e modulo (p – 1) (q – 1). Cela implique que d lorsqu’il est multiplié par e est égal à 1 modulo (p – 1) (q – 1) et d < (p – 1) (q – 1). Il peut être représenté comme : e d = 1 mod (p – 1) (q – 1)
• Notez que cet inverse multiplicatif est le lien entre la clé privée et la clé publique. Bien que les clés ne soient pas dérivées les unes des autres, il existe une relation entre elles.
• Dans notre exemple, nous devons trouver d tel que ce qui précède l’équation est satisfaite. Ce qui signifie, 5 d = 1 mod 96 et aussi d < 96.
• Résolution de plusieurs valeurs de d (peut être calculée en utilisant la version étendue de l’algorithme d’Euclid), nous pouvons voir que d = 77 satisfait notre condition.

Voir les maths : 77 × 5 = 385 et 385 – 1 = 384 est divisible par 96 car 4 × 96 + 1 = 385

• Nous pouvons conclure que le dans notre exemple, la clé privée sera (77, 119).
• Vous avez maintenant vos paires de clés !

Chiffrement/déchiffrement à l’aide de la paire de clés

Une fois les clés générées, le processus de cryptage et de décryptage est assez simple. Le calcul derrière eux est le suivant :

Chiffrer le message en texte clair m pour obtenir le message chiffré c comme suit : c = m . e (mod n) étant donné la clé publique(e, n) et le message en texte clair m.

Décryptage du message chiffré c pour obtenir le message texte clair m est la suivante :

m = c . d (mod n) étant donné la clé privée (d, n) et le texte chiffré c.

Notez que le schéma RSA est un chiffrement de bloc où l’entrée est divisée en petits blocs que l’algorithme RSA peut consommer. En outre, le texte clair et le chiffrement sont tous des entiers de 0 à n – 1 pour certains n entier qui est connu à la fois par l’expéditeur et le récepteur. Cela signifie que le texte clair d’entrée est représenté comme entier, et quand cela passe par RSA et devient un texte chiffré, ils sont à nouveau entiers, mais pas les mêmes que l’entrée; nous les avons cryptés rappelez-vous? Maintenant, compte tenu des mêmes paires de clés de l’exemple précédent, passons par les étapes pour comprendre comment il fonctionne dans la pratique:

• L’expéditeur veut envoyer un message texte au récepteur dont la clé publique est connue et est dit (e, n).
• L’expéditeur décompose le message texte en blocs qui peuvent être représentés comme une série de nombres inférieurs à n.
• Les équivalents de texte chiffré de texte clair peuvent être trouvés en utilisant c = m e (mod n). Si le texte clair (m) est de 19 et la clé publique est (5, 119) avec e = 5 et n = 119, puis le texte chiffré c sera 195 (mod 119) – 2, 476, 099 (mod 119) – 66, qui est le reste et 20 807 est le quotient, que nous n’utilisons pas. Donc, c = 66
• Lorsque le texte chiffré 66 est reçu à l’extrémité du récepteur, il doit être décrypté pour obtenir le texte clair à l’aide de m = c d (mod n).
• Le récepteur a déjà la clé privée (d, n) avec d = 77 et n = 119, et a reçu le text chiffré c = 66 par l’expéditeur. Ainsi, le récepteur peut facilement récupérer le texte clair en utilisant ces valeurs comme m = 6 677 (mod 119) = 19
• Pour les calculs arithmétiques modulaires, il existe de nombreuses calculatrices en ligne que vous pouvez utiliser, tels que: http://comnuan.com/cmnn02/cmnn02008/

Nous avons examiné les mathématiques derrière l’algorithme RSA. Maintenant, nous savons que n (supposé être un très grand nombre) est accessible au public. Bien qu’il soit public, la factorisation de ce grand nombre pour obtenir les nombres premiers p et q est extrêmement difficile. Le régime RSA est basé sur cette difficulté pratique de factorisation de grands nombres. Si p et q ne sont pas assez grands, ou la clé publique e est petite, alors la force de RSA descend. Actuellement, les touches RSA sont généralement entre 1024 et 2048 bits de long. Notez que les frais généraux de calcul de la cryptographie RSA augmente avec la taille des clés.

Dans les situations où la quantité de données est énorme, il est conseillé d’utiliser une technique de cryptage symétrique et de partager la clé en utilisant une technique de cryptage asymétrique comme RSA. En outre, nous avons examiné l’un des aspects de RSA, c’est-à-dire, pour le chiffrement et le décryptage. Cependant, il peut également être utilisé pour l’authentification par signature numérique. Juste pour donner une idée de haut niveau, on peut prendre le hash des données, les signer à l’aide de sa propre clé privée, et le partager avec les données. Le récepteur peut vérifier avec la clé publique de l’expéditeur et s’assurer que c’est l’expéditeur qui a envoyé les données, et non quelqu’un d’autre. De cette façon, en plus de sécuriser le transport clé, la méthode de cryptage à clé publique RSA offre également l’authentification à l’aide d’une signature numérique. Notez ici qu’un algorithme différent appelé algorithme de signature numérique (DSA) peut également être utilisé dans de telles situations que nous allons apprendre dans la section suivante.

RSA est largement utilisé avec HTTPS sur les navigateurs Web, e-mails, VPN, et la télévision par satellite. En outre, de nombreuses applications commerciales ou les applications dans les magasins d’applications sont également signés numériquement en utilisant RSA. SSH utilise également la cryptographie à clé publique ; lorsque vous vous connectez à un serveur SSH, il diffuse une clé publique qui peut être utilisée pour chiffrer les données à envoyer à ce serveur. Le serveur peut alors déchiffrer les données à l’aide de sa clé privée.

Algorithme de signature numérique

Le DSA a été conçu par la NSA dans le cadre de la norme de signature numérique (DSS) et normalisé par le NIST. Notez que son objectif principal est de signer des messages numériquement, et non le chiffrement. Juste pour paraphraser, RSA est à la fois pour la gestion des clés et l’authentification alors que DSA est uniquement pour l’authentification. En outre, contrairement à RSA, qui est basé sur la factorisation grand nombre, DSA est basé sur logarithmes discrets. À un niveau élevé, DSA est utilisé comme indiqué dans la figure 2-15.

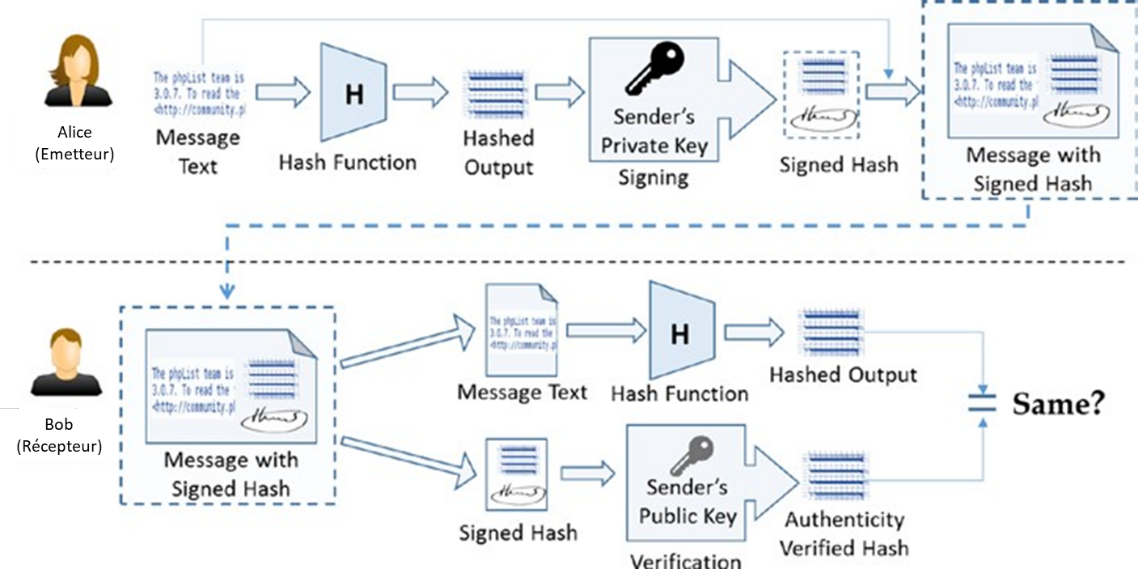
Figure 2-15. Algorithme de signature numérique (DSA)

Comme vous pouvez le voir dans la figure 2-15, le message est d’abord haché, puis signé parce qu’il est plus sécurisé par rapport à la signature, et ensuite son hachage. Idéalement, vous souhaitez vérifier l’authenticité avant de faire toute autre opération. Ainsi, une fois le message signé, le hachage signé est étiqueté avec le message et envoyé au récepteur. Le récepteur peut alors vérifier l’authenticité et trouver le hachage. Aussi, hacher le message pour obtenir le hachage à nouveau et vérifier si les deux hachages correspondent. De cette façon, DSA fournit les propriétés de sécurité suivantes :

• Authenticité : Signée par clé privée et vérifiée par la clé publique
• Intégrité des données : Les hachages ne correspondent pas si les données sont modifiées.
• Non-répudiation : Depuis que l’expéditeur l’a signé, ils ne peuvent pas nier plus tard qu’ils n’ont pas envoyé le message. La non-répudiation est une propriété qui est la plus souhaitable dans les situations où il y a des chances d’un différend sur l’échange de données. Par exemple, une fois qu’une commande est passée électroniquement, l’acheteur ne peut refuser le bon de commande si la non-répudiation est activée dans une telle situation.

Un schéma DSA typique se compose de trois algorithmes : (1) génération de clés, (3) génération de signatures et (3) vérification de signature.

Cryptographie elliptique de courbe

La cryptographie elliptique de courbe (ECC) a réellement évolué la cryptographie de Diffie-Hellman. Il a été découvert comme un mécanisme alternatif pour la mise en œuvre de la cryptographie à clé publique. Il se réfère en fait à une suite de protocoles cryptographiques et est basé sur le problème logarithme discret, comme dans DSA. Cependant, on croit que le problème logarithmique discret est encore plus difficile lorsqu’il est appliqué aux points sur une courbe elliptique. Ainsi, ECC offre une plus grande sécurité pour une taille de clé donnée.

Une clé ECC 160 bits est considérée comme aussi sécurisée qu’une clé RSA 1024 bits. Étant donné que de plus petites tailles de clés dans ECC peuvent fournir une plus grande sécurité et des performances par rapport à d’autres algorithmes de clé publique, il est largement utilisé dans les petits dispositifs embarqués, capteurs, et d’autres dispositifs IoT, etc. Il existe des implémentations matérielles extrêmement efficaces pour ECC.

ECC est basé sur un ensemble mathématiquement lié de nombres sur une courbe elliptique sur les champs finis. En outre, il n’a rien à voir avec les ellipses ! Mathématiquement, une courbe elliptique satisfait les équations :

y² = x³ + ax + b, où 4 a³ + 27 b² ≠ 0

Avec différentes valeurs de “a” et “b“, la courbe prend différentes formes comme indiqué dans le diagramme suivant :

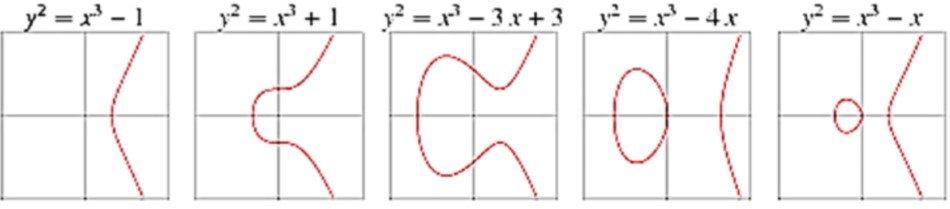
Il existe plusieurs caractéristiques importantes des courbes elliptiques qui sont utilisées dans la cryptographie, telles que :

• Ils sont horizontalement symétriques c’est-à-dire que ce qui se trouve sous l’axe X est une image miroir de ce qui est au-dessus de l’axe X. Ainsi, n’importe quel point sur la courbe une fois reflété au-dessus de l’axe X reste toujours sur la courbe.
• Toute ligne non verticale peut croiser la courbe dans tout aux plus trois endroits.
• Si vous considérez deux points P et Q sur la courbe elliptique et tracez une ligne à travers eux, la ligne peut exactement traverser la courbe à un endroit de plus. Appelons-le (-R). Si vous tracez une ligne verticale à travers (-R), il traversera la courbe à, disons, R, qui est un reflet du point (-R). Maintenant, la troisième propriété implique que P+Q = R. C’est ce qu’on appelle « ajout de points », ce qui signifie que l’ajout de deux points sur une courbe elliptique vous mènera à un autre point sur la courbe. Se référer au diagramme suivant pour une représentation picturale de ces trois propriétés.

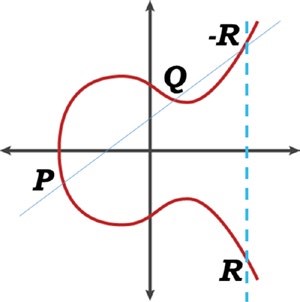
• Ainsi, vous pouvez appliquer l’addition de point à n’importe quels des deux points sur la courbe. Maintenant, nous avons fait l’ajout de point de P et Q (P + Q) et a trouvé –R et finalement arrivé à R. Une fois que nous arrivons à R, nous pouvons alors tracer une ligne de P à R et voir que la ligne croise à nouveau le graphique à un troisième point. Nous pouvons alors prendre ce point et nous déplacer le long d’une ligne verticale jusqu’à ce qu’il croise à nouveau le graphique. Cela devient l’addition de point pour les points P et R. Ce processus avec un P fixé et le point résultant peut continuer aussi longtemps que nous le voulons, et nous allons continuer à obtenir de nouveaux points sur la courbe.
• Maintenant, au lieu de deux points P et Q, que faire si nous appliquons l’opération au même point P, c’est-à-dire, P et P (appelé “point double”). Évidemment, un nombre infini de lignes est possible par P, donc nous ne considérerons que la ligne tangentielle. La ligne tangente traversera la courbe en un point de plus et une ligne verticale à partir de là traversera la courbe à nouveau pour arriver à la valeur finale. Il peut être montré comme suit :

• Il est évident que nous pouvons appliquer le point doublant “n” nombre de fois au point initial et chaque fois qu’il nous mènera à un point différent sur la courbe. La première fois que nous avons appliqué point doublant au point P, il nous a fallu au point résultant 2P comme vous pouvez le voir dans le diagramme. Maintenant, si la même chose est répétée “n” nombre de fois, nous atteindrons un point sur la courbe comme indiqué dans le diagramme suivant :

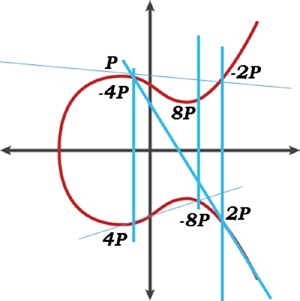
• Dans le scénario susmentionné, lorsque le point initial et final est donné, il n’y a aucun moyen de dire que le doublement de point a été appliqué “n” nombre de fois pour atteindre le point final résultant, sauf en essayant tous les possibles “n” un par un. C’est le problème logarithme discret pour ECC, où il indique que donné un point G et Q, où Q est un multiple de G, trouver “d” tels que Q = d G. Cela forme la fonction à sens unique sans raccourcis. Ici, Q est la clé publique et d est la clé privée. Pouvez-vous extraire la clé privée d de la clé publique Q ?

Il s’agit du problème de logarithme discret de courbe elliptique, qui est difficile à résoudre sur le plan du calcul.

• En outre, la courbe doit être définie sur un champ fini et ne pas nous emmener à l’infini ! Cela signifie que la valeur “max” sur l’axe X doit être limitée à une certaine valeur, il suffit de rouler les valeurs lorsque nous atteignons le maximum. Cette valeur est représentée comme P (pas le P utilisé dans les graphiques ici) dans le cryptosystème ECC et est appelée “modulo” valeur, et il définit également la taille de la clé, d’où le champ fini. Dans de nombreuses implémentations d’ECC, un nombre de premier choix pour “P” est choisi.
• L’augmentation de la taille de “P” se traduit par des valeurs plus utilisables sur la courbe, donc plus de sécurité.
• Nous avons observé que l’ajout de points et le doublement des points constituent la base pour trouver les valeurs qui sont utilisées pour le chiffrement et le décryptage.

Ainsi, pour définir un CCE, les paramètres de domaine suivants doivent être définis :

• L’équation de courbe : y² = x³ + ax + b, où 4 a³ + 27 b² ≠ 0
• P : Le nombre principal, qui spécifie le champ fini que la courbe sera définie (valeur modulo)
• a et b: Coefficients qui définissent la courbe elliptique
• G : Point de base ou point générateur sur la courbe. C’est le point où toutes les opérations ponctuelles commencent et il définit le sous-groupe cyclique.
• n : Le nombre d’opérations ponctuelles sur la courbe jusqu’à la ligne résultante verticale. Donc, c’est l’ordre de G, c’est-à-dire, le plus petit nombre positif de telle sorte que nG = ∞. Il est normalement premier.
• h : Il est appelé «cofacteur», qui est égal à l’ordre de la courbe divisée par n. Il s’agit d’une valeur entière et généralement près de 1.

Notez que ECC est une excellente technique pour générer les clés, mais est utilisé aux côtés d’autres techniques pour les signatures numériques et l’échange de clés. Par exemple, Elliptic Curve Diffie- Hellman (ECDH) est très populairement utilisé pour l’échange de clés et ECDSA est utilisé pour les signatures numériques.

Algorithme de signature numérique Elliptic Curve

L’ECDSA est un type de DSA qui utilise ECC pour la génération de clés. Comme son nom l’indique, son but est la signature numérique, et non le cryptage. ECDSA peut être une meilleure alternative à RSA en termes de taille de clé plus petite, une meilleure sécurité, et des performances plus élevées. C’est l’un des composants cryptographiques les plus importants utilisés dans les Bitcoins !

Nous avons déjà examiné comment les signatures numériques sont utilisées pour établir la confiance entre l’expéditeur et le récepteur. Étant donné que l’authenticité de l’expéditeur et l’intégrité du message peuvent être vérifiées par des signatures numériques, deux parties inconnues peuvent effectuer des transactions entre elles. Notez que l’expéditeur et le récepteur doivent s’entendre sur les paramètres du domaine avant de s’engager dans la communication.

L’ECDSA a largement trois étapes : la génération de clés, la génération de signatures et la vérification des signatures.

Génération clé

Étant donné que les paramètres du domaine (P, a, b, G, n, h) sont préétablis, la courbe et le point de base sont connus par les deux parties. En outre, le premier P qui en fait un champ fini est également connu (P est généralement 160 bits et peut être plus grand ainsi). Ainsi, l’expéditeur, par exemple, Alice fait ce qui suit pour générer les clés :

• Sélectionnez un entier d aléatoire dans l’intervalle [1, n – 1]
• Calcul Q = d G
• Déclarer Q est la clé publique et garder d comme clé privée.

Génération Signature

Une fois les clés générées, Alice, l’expéditeur, utiliserait la clé privée “d” pour signer le message (m). Ainsi, elle effectuerait les étapes suivantes dans l’ordre spécifié pour générer la signature :

• Sélectionnez un nombre aléatoire k dans l’intervalle [1, n – 1]
• Calculer k.G et trouver les nouvelles coordonnées (x₁, y₁) et trouver r = x₁ mod n

Si r = 0, puis recommencer à nouveau

• Calculer e = SHA-1 (m)
• Calculer s = k^-1 (e + d.r) mod n

Si s = 0, puis recommencer à nouveau depuis la première étape

• La signature d’Alice pour le message (m) serait maintenant (r, s)

Vérification de signature

Disons que Bob est le récepteur ici et a accès aux paramètres du domaine et à la clé publique Q de l’expéditrice Alice. Par mesure de sécurité, Bob doit d’abord vérifier que les données dont il dispose, qui sont les paramètres du domaine, la signature et la clé publique Q d’Alice qui sont toutes valides. Pour vérifier la signature d’Alice sur le message (m), Bob effectuerait les opérations suivantes dans l’ordre spécifié :

• Vérifier que r et s sont des entiers dans l’intervalle [1, n – 1]
• Calculer e = SHA-1 (m)
• Calculer w = s^-1 mod n
• Calculer u₁ = e w mod n, et u₂ = r w mod n
• Calculer X = u₁ G + u₂ G, où X représente les coordonnées, par exemple (x₂, y₂)
• Calculer v =x₁ mod n
• Accepter la signature si r = v, sinon le rejeter

Dans cette section, nous avons examiné les mathématiques derrière l’ECDSA. Rappelons que nous avons utilisé un nombre aléatoire tout en générant la clé et la signature. Il est extrêmement important de s’assurer que les nombres aléatoires générés sont en fait cryptographiquement aléatoires. Dans de nombreux cas d’utilisation, 160 bits ECDSA est utilisé parce qu’il doit correspondre à la fonction de hachage SHA-1.

Parmi tant de cas d’utilisation, ECDSA est utilisé dans les certificats numériques. Dans sa forme la plus simple, un certificat numérique est une clé publique, munie de l’ID de l’appareil et de la date d’expiration du certificat. De cette façon, les certificats nous permettent de vérifier et de confirmer à qui appartient la clé publique et l’appareil est un membre légitime du réseau à l’étude. Ces certificats sont très importants pour prévenir les « attaques d’usurpation d’identité » dans les protocoles d’établissement clés. De nombreux certificats TLS sont basés sur la paire de clés ECDSA et cette utilisation continue de croître.

Exemples de code de cryptographie de clé asymétrique

Voici quelques exemples de code de différents algorithmes de clés publiques. Cette section est juste destinée à vous donner une vision sur la façon d’utiliser différents algorithmes. Les exemples de code sont en Python, mais seraient assez similaires dans différentes langues ; vous avez juste à trouver les bonnes fonctions à utiliser dans la bibliothèque.

# -*- coding: utf-8 -*-

import Crypto

from Crypto.PublicKey import RSA

from Crypto import Random

from hashlib import sha256

# Fonction de génération de clés avec pour taille par défaut 1024

def generate_key(KEY_LENGTH=1024):

random_value= Random.new().read

keyPair=RSA.generate(KEY_LENGTH,random_value)

return keyPair

#Génération de clés pour Alice et Bob

bobKey=generate_key()

aliceKey=generate_key()

# Affichage de la clé publique d’Alice et Bob. Cette clé pourrait être partagée

alicePK=aliceKey.publickey()

bobPK=bobKey.publickey()

print “La clé publique d’Alice :”, alicePK

print “La clé publique de Bob :”, bobPK

#Alice veut envoyer un message secret à Bob. Permet de créer un message factice pour Alice

secret_message=” Message secret d’Alice à Bob ”

print “Message”, secret_message

# Fonction pour générer une signature

def generate_signature(key,message):

message_hash=sha256(message).digest()

signature=key.sign(message_hash,”)

return signature

# Permet de générer une signature pour un message secret

alice_sign=generate_signature(aliceKey,secret_message)

# Avant d’envoyer un message sur le réseau, cryptez le message à l’aide de la clé publique de Bob …

encrypted_for_bob = bobPK.encrypt(secret_message, 32)

# Bob déchiffre un message secret à l’aide de sa propre clé privée …

decrypted_message = bobKey.decrypt(encrypted_for_bob)

print “Decrypted message:”, decrypted_message

# Bob utilisera la fonction suivante pour vérifier la signature d’Alice en utilisant sa clé publique

def verify_signature(message,PublicKey,signature):

message_hash=sha256(message).digest()

verify = PublicKey.verify(message_hash,signature)

return verify

# Bob vérifie en utilisant un message décrypté et la clé publique d’Alice

print ” La signature d’Alice pour le message déchiffré est-elle valide?”,

verify_signature(decrypted_message,alicePK, alice_sign)

The ECDSA Algorithm

import ecdsa

# SECP256k1 est la courbe elliptique Bitcoin

signingKey = ecdsa.SigningKey.generate(curve=ecdsa.SECP256k1)

# Obtenir la clé de vérification

verifyingKey = signingKey.get_verifying_key()

# Générer la signature d’un message

signature = signingKey.sign(b”message signé”)

# Vérifier que la signature est valide ou non valide pour un message

verifyingKey.verify(signature, b”message signé”) # Vrai. La signature est valide

# Vérifiez que la signature est valide ou non valide pour un message

assert verifyingKey.verify(signature, b”message”) # Lance une erreur. La signature n’est pas valide pour le message

Échange de clés Diffie-Hellman

Nous avons déjà examiné la cryptographie de clé symétrique dans les sections précédentes. Se rappeler que le partage du secret entre l’expéditeur et le récepteur est un très grand défi. En règle générale, nous sommes maintenant conscients que le canal de communication est toujours insécurisé. Il pourrait toujours y avoir une Eve essayant d’intercepter votre message pendant qu’il est transmis en utilisant différents types d’attaques. Ainsi, la technique de DH a été développée pour échanger en toute sécurité les clés cryptographiques. De toute évidence, vous devez vous demander comment l’échange de clés sécurisé est possible lorsque le canal de communication lui-même est garanti. Eh bien, plus tard dans cette section, nous verrons que la technique DH n’est pas vraiment le partage de la clé secrète entre deux parties, il s’agit plutôt de créer la clé ensemble. À la fin, ce qui est important, c’est que l’expéditeur et le récepteur ont tous deux la même clé. Cependant, gardez à l’esprit qu’il ne s’agit pas d’une cryptographie clé asymétrique, car le chiffrement/décryption n’a pas lieu pendant l’échange. En fait, c’était la base sur laquelle la cryptographie asymétrique de clé a été plus tard conçue. La raison pour laquelle nous examinons cette technique maintenant, c’est parce que beaucoup de mathématiques que nous avons déjà étudié dans la section précédente sont utile ici.

Essayons d’abord de comprendre le concept à un niveau élevé avant d’entrer dans l’explication mathématique. Jetez un œil à ce qui suit (figure 2-16), où une explication simple de l’algorithme DH est présenté avec des couleurs.

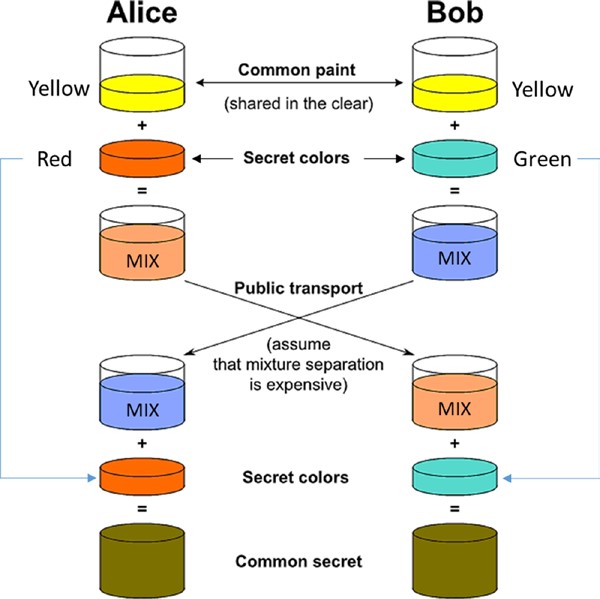
Figure 2-16. Illustration d’échange de clés de Diffie-Hellman

Notez que seule la couleur jaune a été partagée entre les deux parties dans la première étape, ce qui peut représenter toute autre couleur ou un numéro aléatoire. Les deux parties y ajoutent ensuite leur propre secret et en font un mélange. Ce mélange est à nouveau partagé par le même canal garanti. Les partis respectifs y ajoutent alors leur secret et forment leur dernier secret commun. Dans cet exemple avec des couleurs, observez que les secrets communs sont la combinaison des mêmes ensembles de couleurs. Examinons maintenant les étapes mathématiques réelles qui ont lieu pour la génération de clés :

• Alice et Bob s’entendent sur P = 23 et G = 9
• Alice choisit la clé privée a = , calcule 9⁴ mod 23 = 6 et l’envoie à Bob
• Bob choisit la clé privée b = 3, calcule 9³ mod 23 = 16 et l’envoie à Alice
• Alice calcule 16⁴ mod 23 = 9
• Bob calcule 6³ mod 23 = 9

Si vous suivez ces étapes, vous constaterez qu’Alice et Bob sont en mesure de générer la même clé secrète à leurs extrémités qui peuvent être utilisées pour le chiffrement / décryptage. Nous avons utilisé de petits nombres dans cet exemple pour une compréhension facile, mais de grands nombres premiers sont utilisés dans les cas d’utilisation du monde réel. Pour mieux le comprendre, passons en revue l’extrait de code suivant et voyons comment l’algorithme DH peut être implémenté d’une manière simple :

/* Programme pour calculer les clés pour deux parties en utilisant l’algorithme d’échange de clés Diffie-Hellman */

// fonction pour renvoyer la valeur d’a ^ b mod P

long long int power(long long int a, long long int b, long long int P)

{

if (b == 1)

return a;

else

return (((long long int)pow(a, b)) % P);

}

// Programme principal pour le calcul de la clé DH

int main()

{

long long int P, G, x, a, y, b, ka, kb;

// Les deux parties conviennent des clés publiques G et P

P = 23; // Un nombre premier P est pris

printf(“La valeur de P : %lld\n”, P);

G = 9; // Une racine primitive pour P, G est prise

printf(“La valeur de G : %lld\n\n”, G);

// Alice choisira la clé privée a

a = 4; // a est la clé privée choisie

printf(“La clé privée a pour Alice : %lld\n”, a);

x = power(G, a, P); // obtient la clé générée

// Bob choisira la clé privée b

b = 3; // b est la clé privée choisie

printf(“La clé privée b pour Bob : %lld\n\n”, b);

y = power(G, b, P); // obtient la clé générée

// Génération de la clé secrète après l’échange des clés

ka = power(y, a, P); // Clé secrète pour Alice

kb = power(x, b, P); // Clé secrète pour Bob

printf(“La clé secrète d’Alice est : %lld\n”, ka);

printf(“La clé secrète de Bob est : %lld\n”, kb);

return 0;

}

Le problème de logarithme discret est traditionnellement utilisé (le x^y mod p), ainsi le processus général peut être modifié pour utiliser la cryptographie courbe elliptique.

Cryptographie symétrique vs clé asymétrique

Nous avons examiné divers aspects et types d’algorithmes clés symétriques et asymétriques. Évidemment, leurs objectifs de conception et leurs implications sont différents. Faisons une analyse comparative pour que nous utilisions la bonne analyse au bon endroit.

• La cryptographie de clé symétrique est également appelée cryptographie de clé privée. De même, la cryptographie asymétrique de clé est également appelée cryptographie de clé publique.
• L’échange ou la distribution de clés dans la cryptographie de clé symétrique est un grand casse-tête, à la différence de la cryptographie asymétrique de clé.
• Le chiffrement asymétrique est assez exigeant en calcul car la longueur des clés est généralement grande. Par conséquent, le processus de cryptage et de décryptage est plus lent. Au contraire, le chiffrement symétrique est plus rapide.
• La cryptographie de clé symétrique est appropriée pour les messages longs parce que la vitesse de chiffrement/décryptage est rapide. La cryptographie asymétrique des clés est appropriée pour les messages courts, et la vitesse de cryptage/décryptage est lente.
• Dans la cryptographie de clé symétrique, les symboles en texte clair et en texte chiffré sont permutés ou substitués. Dans la cryptographie asymétrique de clé, le texte clair et le chiffrement sont traités comme des entiers.
• Dans de nombreuses situations, lorsque la clé symétrique est utilisée pour le chiffrement et le décryptage, la technique de clé asymétrique est utilisée pour partager et convenir de la clé utilisée dans le chiffrement. La cryptographie de clé asymétrique trouve sa plus forte application dans les environnements non fiables, lorsque les parties impliquées n’ont aucune relation antérieure. Étant donné que les parties inconnues n’ont pas d’occasion préalable d’établir des clés secrètes partagées entre elles, le partage de données sensibles est sécurisé par cryptographie à clé publique.
• Les techniques cryptographiques symétriques ne permettent pas de faire des signatures numériques, qui ne sont possibles que par la cryptographie asymétrique.
• Un autre bon cas est le nombre de clés requises parmi un groupe de nœuds pour communiquer les uns avec les autres. Combien de clés pensez-vous serait nécessaire parmi, disons, 100 participants lorsque la cryptographie clé symétrique est nécessaire ? Ce problème de trouver les clés nécessaires peut être abordé comme un problème graphique complet avec l’ordre 100. Comme chaque vertex nécessite 99 bords connectés pour se connecter avec tout le monde, chaque participant aurait besoin de 99 clés pour établir des connexions sécurisées avec tous les autres nœuds.

Donc, au total, les clés nécessaires seraient 100 * (100 – 1)/2 = 4 950. Il peut être généralisé pour “n” nombre de participants comme n * (n – 1) /2 clés au total. Avec un nombre accru de participants, cela devient un cauchemar ! Toutefois, dans le cas de la cryptographie asymétrique, chaque participant n’aurait besoin que de deux clés (une privée et une publique). Pour un réseau de 100 participants, le nombre total de clés nécessaires ne serait que de 200. Le tableau 2-5 montre certains exemples de données pour vous donner une analogie sur le nombre accru de touches nécessaires lorsque le nombre de participants augmente.

Tableau 2-5. Comparaison des exigences clés pour les techniques clés asymétriques

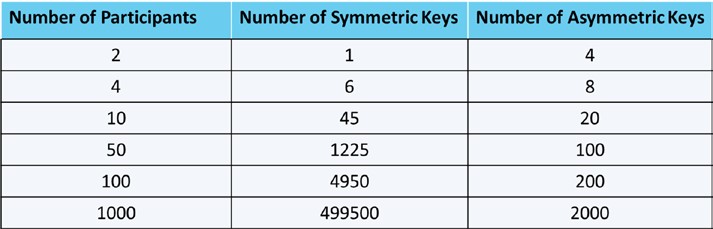
Théorie du jeu

La théorie du jeu est un concept assez ancien et est utilisé dans de nombreuses situations de la vie réelle pour résoudre des problèmes complexes. La raison pour laquelle nous couvrons ce sujet est parce qu’elle est utilisée dans les Bitcoins et de nombreuses autres solutions blockchain. elle a été officiellement présentée par John von Neumann pour étudier les décisions économiques. Plus tard, il a été plus popularisé par John Forbes Nash Jr en raison de sa théorie de “Nash Equilibrium”, que nous examinerons sous peu. Comprenons d’abord ce qu’est la théorie des jeux.

La théorie du jeu est une théorie sur les jeux, où les jeux ne sont pas seulement ce que les enfants jouent. La plupart sont des situations où deux parties ou plus sont impliquées dans un certain comportement stratégique.

Exemples : Un tournoi de cricket est un jeu, deux parties en conflit dans une cour de justice avec des avocats et des jurys est un jeu, deux frères et sœurs se battent pour une crème glacée est un jeu, une élection politique est un jeu, un signal de circulation est aussi un jeu. Un autre exemple : Disons que vous avez postulé pour un emploi blockchain et vous êtes sélectionné, on vous propose un emploi avec un certain salaire, mais vous rejetez l’offre, pensant qu’il y a un écart énorme dans la demande et l’offre et que les chances sont bonnes, ils vont réviser l’offre avec un salaire plus élevé. Vous devez penser maintenant, ce qui n’est pas un jeu ? Eh bien, dans des situations réelles, presque tout est un jeu. Ainsi, un « jeu » peut être défini comme une situation impliquant un « choix rationnel corrélé ». Ce que cela signifie, c’est que les perspectives disponibles pour n’importe quel joueur dépendent non seulement de leurs propres choix, mais aussi des choix que d’autres font dans une situation donnée. En d’autres termes, si votre destin est affecté par les actions des autres, alors vous êtes dans un jeu. Alors, qu’est-ce que la théorie des jeux ?

La théorie des jeux est une étude des stratégies impliquées dans des jeux complexes. C’est l’art de faire le meilleur geste, ou d’opter pour une meilleure stratégie dans une situation donnée basée sur l’objectif. Pour ce faire, il faut comprendre la stratégie de l’adversaire et aussi ce que l’adversaire pense que votre mouvement va être. Prenons un exemple simple : il y a deux frères et sœurs, l’un aîné et l’autre plus jeune. Maintenant, il y a deux crèmes glacées dans le réfrigérateur, l’un est saveur d’orange et l’autre est la saveur de mangue. L’aîné veut manger la saveur d’orange, mais sait s’il opte pour cela, alors le plus jeune pleurerait pour la même orange. Donc, il opte pour la crème glacée aromatisée à la mangue et il s’avère que comme prévu, le plus jeune veut la même chose. Maintenant, l’aîné prétend avoir sacrifié la crème glacée aromatisée à la mangue et la donne au plus jeune et mange l’orange lui-même. Regardez la situation : c’est gagnant-gagnant pour les deux parties, car c’était l’objectif de l’aîné. Si l’aîné voulait, il aurait tout simplement pu se battre avec le plus jeune enfant et obtenir l’orange si c’était son objectif. Dans le deuxième cas, l’aîné élaborerait des stratégies pour que le plus jeune ne soit pas blessé, mais assez pour qu’il abandonne la crème glacée aromatisée à l’orange. C’est la théorie du jeu : quel est votre objectif et quel devrait être votre meilleur coup ?

Un autre exemple : plus sur le plan commercial cette fois. Imaginez que vous êtes un vendeur fournissant des légumes à une ville. Il y a, disons, trois façons de se rendre à la ville, dont l’une est un itinéraire régulier dans le sens où tout le monde va par cette voie, peut-être parce qu’il est plus court et mieux. Un jour, vous voyez que l’itinéraire régulier a été bloqué en raison d’une certaine activité de réparation et en aucun cas vous ne pouvez passer par cette route. Il vous reste deux autres itinéraires. L’un d’eux est un court itinéraire vers la ville de destination, mais est un peu étroit. L’autre est un peu plus long mais assez large. Ici, vous devez faire une stratégie quant à l’itinéraire que vous devez choisir. La situation peut être telle qu’il y a un trafic dense sur les routes et que beaucoup de gens essaieraient de traverser la route la plus courte. Cela peut entraîner une congestion importante sur cette route et peut causer un énorme retard. Donc, vous avez décidé de prendre la route plus longue pour atteindre la ville à temps, mais au prix de quelques dollars supplémentaires dépensés en carburant. Vous êtes sûr que vous pouvez facilement compenser pour cela si vous arrivez à l’heure et vendez vos légumes plus tôt à un bon prix. C’est la théorie du jeu : quel est votre meilleur coup pour l’objectif que vous avez à l’esprit, qui est généralement de trouver une solution optimale.

Dans de nombreuses situations, le rôle que vous jouez et votre objectif jouent tous deux un rôle essentiel dans la formulation de la stratégie. Exemple : Si vous êtes un organisateur d’un événement sportif et non un participant à la compétition, alors vous formuleriez une stratégie où votre objectif pourrait être que vous vouliez que les participants respectent les règles et respectent le protocole. C’est parce que vous ne vous souciez pas qui gagne à la fin, vous êtes juste un organisateur. D’autre part, un participant élaborerait une stratégie pour les coups gagnants en tenant compte des forces et des faiblesses de l’adversaire, et des règles imposées par l’organisateur parce qu’il pourrait y avoir des pénalités si vous enfreignez les règles. Maintenant, considérons cette situation avec vous jouant le rôle de l’organisateur. Vous devriez considérer s’il pouvait y avoir une situation où un participant enfreint une règle et perd un point, mais blesse l’adversaire et ne permet pas de concourir plus longtemps. Vous devez donc tenir compte de ce que les participants peuvent penser et établir vos règles en conséquence.

Essayons de définir la théorie des jeux une fois de plus sur la base de ce que nous avons appris des exemples précédents. C’est la méthode de modélisation des situations réelles sous la forme d’un jeu et l’analyse de la meilleure stratégie ou le mouvement d’une personne ou d’une entité pourrait être dans une situation donnée pour un résultat souhaité. Les concepts de la théorie des jeux sont largement utilisés dans presque tous les aspects de la vie, tels que la politique, les médias sociaux, l’urbanisme, les enchères, les paris, le marketing, le stockage distribué, l’informatique distribuée, les chaînes d’approvisionnement et les finances, pour n’en nommer que quelques-uns. En utilisant des concepts théorétiques de jeu, il est possible de concevoir des systèmes où les participants jouent selon les règles sans assumer les valeurs émotionnelles ou morales d’entre elles. Si vous voulez aller au-delà de la simple construction d’une preuve de concept et d’obtenir votre produit ou une solution à la production, alors vous devriez prioriser la théorie des jeux comme l’un des éléments les plus importants. Elle peut vous aider à créer des solutions robustes et vous permet de tester ceux avec différents scénarios intéressants. Eh bien, beaucoup de gens pensent déjà dans les perspectives théoriques du jeu sans savoir que c’est la théorie du jeu. Cependant, si vous êtes équipé avec les nombreux outils et techniques de la théorie des jeux, elle peut certainement vous aider.

Équilibre Nash

Dans la section précédente, nous avons examiné différents exemples de jeux. Il existe de nombreuses façons de classer les jeux, tels que les jeux coopératifs/non coopératifs, les jeux symétriques/asymétriques, les jeux à somme nulle/non-somme nulle, les jeux simultanés/séquentiels, etc. Plus généralement, concentrons-nous ici sur la perspective coopérative/non coopérative, parce qu’elle est liée à l’équilibre de Nash.

Comme son nom l’indique, les joueurs coopèrent les uns avec les autres et peuvent travailler ensemble pour former une alliance dans les jeux coopératifs. En outre, il peut y avoir une certaine force externe appliquée pour assurer le comportement coopératif entre les joueurs. D’autre part, dans les jeux non coopératifs, les joueurs rivalisent en tant qu’individus sans possibilité de former une alliance. Les participants ne font que s’occuper de leurs propres intérêts. En outre, aucune force externe n’est disponible pour faire respecter le comportement coopératif.

L’équilibre de Nash indique que, dans tous les jeux non coopératifs où les joueurs connaissent les stratégies de l’autre, il existe au moins un équilibre où tous les joueurs jouent leurs meilleures stratégies pour obtenir le maximum de profits et dont aucun joueur ne bénéficierait en changeant sa stratégie. Si vous connaissez les stratégies d’autres joueurs et que vous avez votre propre stratégie aussi, si vous ne pouvez pas bénéficier du changement de votre propre stratégie, alors c’est l’état de l’équilibre Nash. Ainsi, chaque stratégie dans un équilibre de Nash est une meilleure réponse à toutes les autres stratégies dans cet équilibre.

Notez qu’un joueur peut élaborer des stratégies pour gagner en tant que joueur individuel, mais pas pour vaincre l’adversaire en assurant le pire pour les adversaires. En outre, n’importe quel jeu lorsqu’il est joué à plusieurs reprises peut éventuellement tomber dans l’équilibre Nash.

Dans la section suivante, nous examinerons le « dilemme des prisonniers » pour obtenir une compréhension concrète de l’équilibre de Nash.

Dilemme du prisonnier

Beaucoup de jeux dans la vie réelle peuvent également être des jeux à non-somme nulle. Le dilemme du prisonnier en est un exemple, qui peut être largement qualifié de jeu symétrique. C’est parce que, si vous changez l’identité des joueurs (par exemple, si deux joueurs “A” et “B” jouent, puis “A” devient “B” et “B” devient “A”), et aussi les stratégies ne changent pas, alors le gain reste le même. C’est ce qu’est un jeu symétrique.

Commençons directement par un exemple. Supposons qu’il y a deux gars, Bob et Charlie, qui sont pris par les flics pour la vente de drogues de façon indépendante, par exemple dans des endroits différents. Ils sont gardés dans deux cellules différentes pour interrogatoire. On leur a alors dit qu’ils seraient condamnés à deux ans de prison pour ce crime. Les flics soupçonnent que ces deux gars pourraient aussi être impliqués dans le vol qui vient de se produire la semaine dernière. S’ils n’ont pas commis le vol, c’est de toute façon deux ans d’emprisonnement. Donc, les flics doivent élaborer une stratégie pour arriver à la vérité. Voici donc ce qu’ils font.

Les flics vont voir Bob et lui donnent le choix, un bon choix qui va comme ça. Si Bob avoue son crime et Charlie ne le fait pas, alors sa peine passerait de deux ans à seulement un an et Bob obtient cinq ans. Cependant, si Bob nie et Charlie avoue, alors Bob obtient cinq ans et Charlie obtient juste un an. Aussi, si les deux avouent, alors les deux obtiennent trois ans d’emprisonnement. De même, le même choix est donné à Charlie ainsi. Que pensez-vous qu’ils vont faire ? Cette situation est appelée le dilemme du prisonnier.

Bob et Charlie sont dans deux cellules différentes. Ils ne peuvent pas se parler et conclure avec la situation où ils nient et obtiennent deux ans de prison (juste pour l’affaire de trafic de drogue), ce qui semble être la solution optimale dans cette situation. Même s’ils pouvaient se parler, ils ne se font peut-être pas vraiment confiance.

Qu’est-ce qui passerait dans l’esprit de Bob maintenant ? Il a deux choix, confesser ou nier. Il sait que Charlie choisirait ce qui est le mieux pour lui, et lui-même n’est pas différent. S’il nie et Charlie avoue, alors il est en difficulté en obtenant cinq ans de prison et Charlie obtient juste un an de prison. Il ne veut certainement pas se retrouver dans cette situation.

Si Bob avoue, alors Charlie a deux choix : avouer ou nier. Maintenant Bob pense que s’il avoue, alors quoi que Charlie fasse, il n’a pas plus de trois ans. Énonçons ces scénarios pour Bob.

• Bob avoue et Charlie nie-Bob obtient un an, Charlie obtient cinq ans (meilleur cas étant donné si Bob avoue)
• Bob avoue et Charlie avoue aussi-Bob et Charlie obtenir trois ans (le pire des cas étant donné si Bob avoue)

Cette situation est appelée équilibre Nash où chaque partie a pris la meilleure option, étant donné les choix de l’autre partie. Ce n’est certainement pas l’optimum global, mais représente le meilleur choix en tant qu’individu. Maintenant, si vous regardez cette situation comme un étranger, vous diriez que les deux devraient nier et obtenir deux ans. Mais quand vous jouez en tant que participant dans le jeu, l’équilibre Nash est ce que vous finiriez par faire. Notez que c’est l’étape la plus stable où vous changez votre décision qui ne vous bénéficie pas du tout. Il peut être représenté de façon picturale comme le montre la figure 2-17.

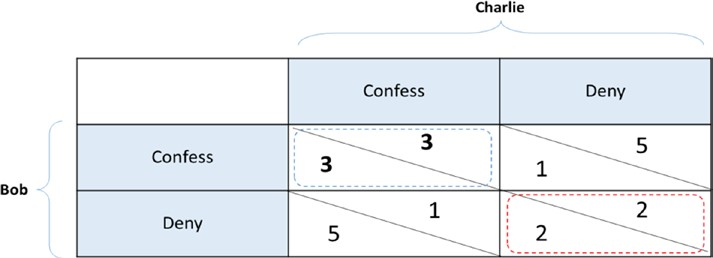
Figure 2-17. Le dilemme du prisonnier—matrice des sentences

Problème des généraux byzantins

Dans la section précédente, nous avons examiné différents exemples de jeux et appris quelques concepts de théorie des jeux. Maintenant, nous allons discuter d’un problème spécifique de l’ancien temps qui est encore largement utilisé pour résoudre de nombreux problèmes informatiques ainsi que des problèmes de la vie réelle.

Le problème des généraux byzantins était un problème rencontré par l’armée byzantine en attaquant une ville. La situation était simple mais très difficile à gérer. En d’autres termes, la situation était que plusieurs factions de l’armée commandées par des généraux distincts entouraient une ville pour la conquérir. La seule chance de victoire est quand tous les généraux attaquent la ville ensemble. Cependant, le problème est de savoir comment parvenir à un consensus. Cela implique que tous les généraux devraient attaquer ou tous devraient battre en retraite. Si certains d’entre eux attaquent et se retirent, alors les chances sont plus grandes qu’ils perdent la bataille. Prenons l’exemple avec des chiffres pour mieux comprendre la situation.

Supposons une situation où il y a cinq factions de l’armée byzantine qui entourent une ville. Ils attaqueraient la ville si au moins trois généraux sur cinq sont prêts à attaquer, mais se retireraient autrement. S’il y a un traître parmi les généraux, ce qu’il peut faire, c’est voter pour l’attaque avec les généraux prêts à attaquer et à voter pour la retraite avec les généraux prêts à battre en retraite. Il peut le faire parce que l’armée est dispersée en factions, ce qui rend la coordination centralisée difficile. Cela peut entraîner deux généraux d’attaquer la ville et de se retrouver en infériorité numérique et d’être vaincu. Il pourrait y avoir des problèmes plus compliqués avec une telle situation :

• Et s’il y a plus d’un traître ?
• Comment la coordination des messages entre généraux aurait-elle lieu ?
• Que se passe-t-il si un messager est capturé/tué/soudoyé par le commandant de la ville ?
• Et si un général traître envoie un message différent et trompe les autres généraux ?
• Comment trouver les généraux qui sont honnêtes et ceux qui son des traîtres ?

Comme vous pouvez le voir, il y a tant de défis qui doivent être relevés pour une attaque coordonnée sur la ville. Il peut être représenté de façon picturale comme dans la figure 2-18.

Figure 2-18. Armée byzantine attaquant la ville

Il existe de nombreux scénarios dans la vie réelle qui sont analogues au problème des généraux byzantins. La façon dont un groupe de personnes parvient à un consensus sur un ordre du jour ou sur la façon de maintenir l’état cohérent d’une base de données distribuée ou décentralisée, ou le maintien de l’état cohérent des copies de la blockchain à travers les nœuds d’un réseau sont quelques exemples similaires au problème des généraux byzantins. Notez, cependant, que les solutions à ces différents problèmes pourraient être très différentes dans différentes situations. Nous examinerons comment Bitcoin résout le problème des généraux byzantins dans cet article.

Jeux De Somme Zéro

Un jeu à somme nulle dans la théorie du jeu est assez simple. Dans de tels jeux, le gain d’un joueur est équivalent à la perte d’un autre joueur. Exemple : On gagne exactement le même montant que l’adversaire perd, ce qui signifie que les choix des joueurs ne peuvent ni augmenter ni diminuer les ressources disponibles dans une situation donnée.

Poker, échecs, go, etc. sont quelques exemples de jeux à somme nulle. Pour généraliser encore plus, les jeux où une seule personne gagne et l’adversaire perd, comme le tennis, le badminton, etc. sont également des jeux à somme nulle. De nombreux instruments financiers tels que les swaps, les contrats à terme et les options peuvent également être décrits comme des instruments à somme nulle.

Dans de nombreuses situations réelles, les gains et les pertes sont difficiles à quantifier. Ainsi, les jeux à somme nulle sont moins fréquents par rapport aux jeux non à somme nulle. La plupart des transactions financières ou des métiers et le marché boursier sont des jeux à somme non nulle. L’assurance, cependant, est un domaine où un jeu à somme nulle joue un rôle important. Il suffit de penser à la façon dont les régimes d’assurance fonctionnent. Nous payons une prime d’assurance aux compagnies d’assurance pour nous prémunir contre certaines situations difficiles telles que les accidents, l’hospitalisation, la mort, etc. Pensant que nous sommes assurés, nous vivons une vie paisible et nous sommes équitablement compensés par les compagnies d’assurance lorsque nous faisons face à des situations difficiles.

Vous pouvez demander s’il est utile d’étudier les jeux à somme nulle. Le simple fait d’être conscient d’une situation à somme nulle est très utile pour comprendre et élaborer une stratégie pour tout problème complexe. Nous pouvons analyser si nous pouvons pratiquement gagner dans une situation donnée dans laquelle les transactions ont lieu.

Pourquoi étudier la théorie des jeux

La théorie des jeux est un phénomène interdisciplinaire révolutionnaire réunissant la psychologie, l’économie, les mathématiques, la philosophie et un vaste mélange de divers autres domaines académiques.

Nous disons que la théorie des jeux est liée à des problèmes du monde réel. Cependant, les problèmes sont illimités. Les concepts théorétiques du jeu sont-ils également illimités ? Certainement ! Nous utilisons la théorie des jeux tous les jours, sciemment ou inconsciemment, parce que nous utilisons toujours notre cerveau pour prendre la meilleure action stratégique, compte tenu d’une situation. N’est-ce pas ? Si c’est le cas, pourquoi étudier la théorie des jeux ?

Eh bien, il existe de nombreux exemples dans la théorie des jeux qui nous aident à penser différemment. Il y a quelques théories développées telles que l’équilibre de Nash qui se rapportent à de nombreuses situations de la vie réelle. Dans de nombreuses situations réelles, les participants ou les acteurs sont confrontés à une matrice de décision similaire à celle d’un « dilemme du prisonnier ». Ainsi, l’apprentissage de ces concepts nous aide non seulement à formuler les problèmes d’une manière plus mathématique, mais permet également de nous faire prendre la meilleure décision. Il nous permet d’identifier les aspects que chaque participant devrait prendre en considération avant de choisir une décision stratégique dans une interaction donnée. Il nous dit d’identifier le type de jeu en premier ; qui sont les joueurs, quels sont leurs objectifs ou buts, quelles pourraient être leurs actions, etc., pour être en mesure de prendre la meilleure décision. Beaucoup de prise de décision dans la vie réelle implique différentes parties ; la théorie des jeux fournit la base d’une prise de décision rationnelle.

Le problème des généraux byzantins que nous avons étudiés dans la section précédente est largement utilisé dans les solutions de stockage distribuées et les centres de données pour maintenir la cohérence des données entre les nœuds informatiques.

Ingénierie informatique

Comme mentionné déjà, il est l’ingénierie intelligente avec les concepts de l’informatique qui lie les composants de la cryptographie, la théorie des jeux, et bien d’autres pour construire une blockchain. Dans cette section, nous allons apprendre quelques-uns des composants importants de l’informatique qui sont utilisés dans la blockchain.

La Blockchain

Comme nous le verrons, une blockchain est en fait une structure de données blockchain ; dans le sens où il s’agit d’une chaîne de blocs reliés entre elles. Lorsque nous disons un bloc, cela peut signifier juste une seule transaction ou plusieurs transactions ensemble. Nous allons commencer notre discussion avec des pointeurs de hayons, qui est le bloc de base de la structure de données blockchain.

Un pointeur de hachage est un hachage cryptographique pointant vers un bloc de données, où le pointeur de hachage est le hachage du bloc de données lui-même (figure 2-19). Contrairement aux listes liées qui pointent vers le bloc suivant afin que vous puissiez y arriver, les pointeurs de hachage pointent vers le bloc de données précédent et fournissent un moyen de vérifier que les données n’ont pas été falsifiées.

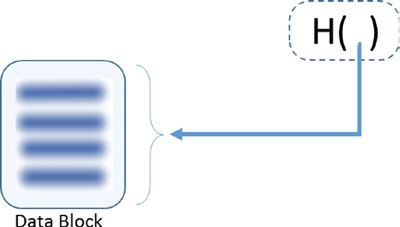
Figure 2-19. Pointeur de hachage pour un bloc de transactions

Le but du pointeur de hachage est de construire une blockchain résistante à la falsification qui peut être considérée comme une source unique de vérité. Comment la blockchain atteint-elle cet objectif ? La façon dont il fonctionne est que le hachage du bloc précédent est stocké dans l’en-tête du bloc courant, et le hachage du bloc courant avec son en-tête de bloc sera stocké dans l’en-tête du bloc suivant. Cela crée la blockchain comme nous pouvons le voir dans la figure 2-20.

Figure 2-20. Blocs dans une blockchain reliée par des pointeurs de hachage

Comme nous pouvons l’observer, chaque bloc indique son bloc précédent, connu sous le nom de « bloc parent ». Chaque nouveau bloc qui est ajouté à la chaîne devient le bloc parent pour le bloc suivant à ajouter. Cela va de toute les façon vers le premier bloc qui est créé dans la blockchain, qui est appelé “le bloc de genèse.” Dans une telle conception où les blocs sont liés à des hachage, il est pratiquement impossible pour quelqu’un de modifier les données dans n’importe quel bloc. Nous avons déjà examiné les propriétés des fonctions de hachage, donc nous comprenons que les hachages ne correspondent pas si les données sont modifiées. Que faire si quelqu’un change le hachage ? Concentrons-nous sur la figure 2-21 pour comprendre comment il n’est pas possible de modifier les données de quelque façon que ce soit.

Figure 2-21. Toute tentative de modification du contenu Header ou Block casse toute la chaîne. Supposons que vous avez modifié les données dans le bloc-1234. Si vous le faites, le hachage qui est stocké dans l’en-tête de bloc du bloc-1235 ne correspondrait pas.

• Que faire si vous modifiez également le hachage stocké dans l’en-tête de bloc du bloc-1235 de sorte qu’il correspond parfaitement aux données modifiées. En d’autres termes, vous hachez le bloc de données-1234 après que vous le modifiez et remplacez ce nouveau hachage par celui stocké dans l’en-tête du bloc-1235. Après cela, le hachage du bloc-1235 change (parce que le bloc-1235 signifie les données et l’en-tête ensemble) et il ne correspond pas à celui stocké dans l’en-tête de bloc du bloc-1236.
• Il faut continuer à faire cela jusqu’à la fin ou le hachage le plus récent. Puisque tout le monde ou beaucoup dans le réseau ont déjà une copie de la blockchain avec le hachage le plus récent, en aucun cas il n’est possible de pirater la majorité des systèmes et de changer tous les hachage à la fois.
• Cela en fait une structure de données blockchain inviolable.

Cela signifie clairement que chaque bloc peut être identifié de façon unique par son hachage. Pour calculer ce hachage, vous pouvez utiliser la famille SHA2 ou SHA3 des fonctions de hachage que nous avons discuté dans la section cryptographie. Si vous utilisez SHA-256 pour hacher les blocs, il produirait une sortie de hachage 256 bits tels que :

0000000000000000a73b6a2af7bad40ec3fc2a83dafd76ef15f3d1b71a71132765

Admmettons qu’il n’y a que 64 caractères en elle. Étant donné que la sortie hachée est représentée à l’aide de caractères hexadécimaux, et que chaque chiffre hexagonal peut être représenté en quatre bits, la sortie est de 64 x 4 = 256 bits. Vous verriez habituellement que la sortie hachée de 256 bits est représentée en utilisant les 64 caractères hexagonaux dans de nombreux endroits.

La structure d’un bloc, c’est-à-dire la taille du bloc, les sections de données et d’en-tête, le nombre de transactions dans un bloc, etc., sont quelque chose que vous devriez décider lors de la conception d’une solution blockchain. Pour les blockchains existantes telles que Bitcoin, Ethereum ou Hyperledger, la structure est déjà définie et vous devez comprendre que pour construire sur ces plates-formes. Nous examinerons de plus près les blockchains Bitcoin et Ethereum plus tard dans l’article.

Arbres de Merkle

Un arbre Merkle est un arbre binaire de pointeurs de hachage cryptographique, donc il est un arbre de hachage binaire. Il est nommé ainsi d’après son inventeur Ralph Merkle. Il s’agit d’une autre structure de données utile utilisée dans les solutions blockchain telles que Bitcoin. Les arbres de merkle sont construits par le hachage des données appariées (généralement des transactions au niveau des feuilles), puis à nouveau hachant les sorties hachées tout le chemin jusqu’au nœud racinaire, appelé la racine de Merkle. Comme tout autre arbre, il est construit de bas en haut. Dans Bitcoin, les feuilles sont toujours des transactions d’un seul bloc dans une blockchain. Nous allons discuter dans peu de temps les avantages de l’utilisation des arbres Merkle, de sorte que vous puissiez décider par vous-même si les feuilles sont des transactions ou un groupe de transactions en blocs. Un arbre Merkle typique peut être représenté comme dans la figure 2-22.

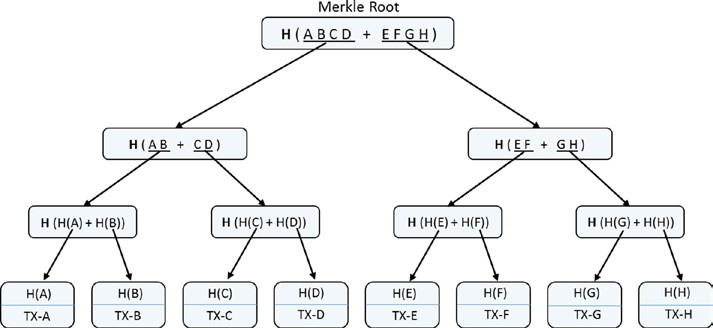
Figure 2-22. Représentation d’arbre de Merkle

Semblable à la structure de données du pointeur de hachage, l’arbre merkle est également inviolable. La falsification à n’importe quel niveau dans l’arbre ne correspondrait pas au hachage stocké à un niveau supérieur dans la hiérarchie, et aussi jusqu’au nœud racine. Il est vraiment difficile pour un hacker de changer tous les hachages dans l’arbre entier. Il assure également l’intégrité de l’ordre des transactions. Si vous changez juste l’ordre des transactions, alors tous les hachages dans l’arbre jusqu’à la racine de Merkle doivent changer.

Voici une situation. L’arbre Merkle est un arbre binaire et il devrait y avoir un nombre pair d’éléments au niveau des feuilles. Que se passe-t-il s’il y a un nombre impair d’articles ? Une bonne solution serait de dupliquer le dernier hachage de transaction. Puisque c’est le hachage que nous dupliquons, cela signifierait juste la même transaction et ne créerait aucun problème tel que la double dépense ou les transactions répétées. De cette façon, il est possible d’équilibrer l’arbre.

Dans la blockchain dont nous avons discuté, si nous devions trouver une transaction par le biais de son hachage, ou vérifier si une transaction s’était produite dans le passé, comment pourrions-nous arriver à cette transaction ? La seule façon est de continuer à traverser jusqu’à ce que vous rencontriez le bloc exact qui correspond au hachage de la transaction. C’est un cas où un arbre de Merkle peut aider beaucoup.

Les arbres merkle offrent un moyen très efficace de vérifier si une transaction spécifique appartient à un bloc particulier. S’il y a des transactions « n » dans un arbre Merkle (éléments de feuilles), alors cette vérification prend seulement du temps de journal (n) comme indiqué dans la figure 2-23.

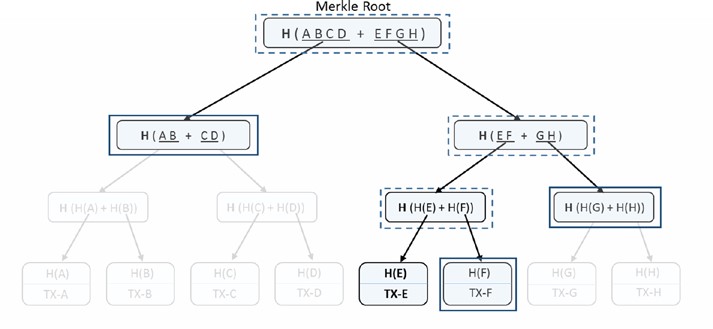
Figure 2-23. Vérification dans l’arbre de Merkle

Pour vérifier si une transaction ou tout autre élément feuille appartient à un arbre de Merkle, nous n’avons pas besoin de tous les éléments et de l’arbre entier. Au contraire, un sous-ensemble de celui-ci est nécessaire comme nous pouvons le voir dans le diagramme de la figure 2-23. On peut juste commencer par la transaction à vérifier avec son frère (c’est un arbre binaire donc il y a un élément de feuille frère), calculer le hachage de ces deux, et voir s’il correspond à leur hachage parent. Ensuite, continuez avec ce hachage parent et son frère à ce niveau et les hacher ensemble pour obtenir leur hachage parent.

Poursuivre ce processus jusqu’au hachage racine supérieur est la plus rapide possibilité de vérification des transactions (il suffit de log (n) time for n items). Dans la figure, seuls les rectangles pleins sont requis et les rectangles en pointillés peuvent être simplement calculés, à condition que les données du rectangle plein. Puisqu’il y a huit éléments de transaction (n = 8), seulement trois calculs (log2 8 = 3) serait nécessaire pour la vérification.

Maintenant, que diriez-vous d’un hybride de la structure de données blockchain et de l’arbre de Merkle? Imaginez une situation dans une blockchain où chaque bloc a beaucoup de transactions. Comme il s’agit d’une blockchain, le hachage du bloc précédent est déjà là ; maintenant, y compris la racine Merkle de toutes les transactions dans un bloc peut aider à une vérification plus rapide des transactions. Si nous devons vérifier une transaction qui est prétendue provenir, disons, du bloc-22456, nous pouvons obtenir les transactions de ce bloc, vérifier l’arbre Merkle et confirmer rapidement si cette transaction est valide. Nous avons déjà vu que la vérification d’une transaction est assez facile et rapide avec les arbres Merkle. Bien que les blocs de la blockchain soient inviolables et ne fournissent même pas la moindre marge de manœuvre pour changer quoi que ce soit dans un bloc, l’arbre Merkle garantit également que l’ordre des transactions est préservé.

Dans un paramètre blockchain typique, il pourrait y avoir de nombreuses situations où un nœud (par souci de simplicité, suppose tout nœud qui n’a pas les données complètes de la blockchain, c’est-à-dire un nœud léger) doit vérifier si une certaine transaction a eu lieu dans le passé. Il y a en fait deux choses qui doivent être vérifiées ici : la transaction dans le cadre du bloc, et le bloc dans le cadre de la blockchain. Pour ce faire, un nœud n’a pas à télécharger toutes les transactions d’un bloc, il peut simplement demander au réseau pour les informations relatives au hachage du bloc et le hachage de la transaction. Les pairs du réseau qui disposent des informations pertinentes peuvent répondre avec l’arbre de Merkle à cette transaction. Eh bien, vous pourriez demander comment faire confiance aux données qu’un « peer » inconnu dans le réseau partage avec vous. Vous savez déjà que les fonctions de hachage sont à sens unique. Ainsi, en aucun cas un nœud contradictoire ne peut forger des transactions qui correspondraient à une valeur de hachage donnée; il est même difficile de le faire du niveau de la transaction jusqu’à la racine de Merkle.

L’utilisation des arbres Merkle ne se limite pas aux blockchains : elles sont largement utilisées dans de nombreuses autres applications telles que BitTorrent, Cassandra, une base de données NoSQL, Apache Wave, etc.

Exemple Code Snippet pour Merkletree

Cette section est juste destinée à vous donner une vision sur la façon de coder un arbre Merkle à son niveau le plus basique. Les exemples de code sont en Python, mais seraient assez similaires dans différentes langues ; vous avez juste à trouver les bonnes fonctions à utiliser dans la bibliothèque.

# -*- coding: utf-8 -*-

from hashlib import sha256

class MerkelTree(object):

def __init__(self):

pass

def chunks(self,transaction,n):

# Cette fonction génère un nombre « n » de transactions à la fois

for i in range (0, len(transaction),number):

yield transaction[i:i+2]

def merkel_tree(self,transactions):

# Ici, nous trouverons le hachage de l’arbre merkel de toutes les transactions passées à cette fonction

#Le Problème est résolu en utilisant la technique de récursivité

# Étant donné une liste de transactions, nous concaténons les hachages par groupes de deux et calculons le hachage du groupe, puis nous gardons le hachage du groupe. Nous répétons cette étape jusqu’à atteindre un seul hachage

sub_tree=[]

for i in chunks(transactions,2):

if len(i)==2:

hash = sha256(str(i[0]+i[1])).hexdigest()

else:

hash = sha256(str(i[0]+i[0])).hexdigest()

sub_tree.append(hash)

# Lorsque le sous-arbre n’a qu’un seul hachage, nous avons atteint notre hachage d’arbre merkel.

# Sinon, nous appelons cette fonction récursivement

if len(sub_tree) == 1:

return sub_tree[0]

else:

return self.merkel_tree(sub_tree)

if __name__==’__main__’:

mk=MerkelTree()

merkel_hash= mk.merkel_tree([“TX1″,”TX2″,”TX3″,”TX4″,”TX5″,”TX6”])

print merkel_hash

Mêlons tout cela ensemble

Pour arriver à cette section, nous avons couvert tous les composants nécessaires de la blockchain qui peuvent nous aider à comprendre comment elle fonctionne vraiment. Après les avoir passés en revue, à savoir la cryptographie, la théorie des jeux et les concepts d’ingénierie informatique, nous devons avoir développé une notion de fonctionnement des blockchains. Bien que ces concepts aient été autour depuis des siècles, personne ne pourrait jamais imaginer comment les mêmes vieux trucs peuvent être utilisés pour construire une technologie de transformation comme la blockchain. Faisons un bref récapitulatif de certains principes fondamentaux que nous avons abordés jusqu’à présent, et nous allons approfondir la compréhension de ces concepts.

Donc, les voici:

• Les fonctions cryptographiques sont à sens unique et ne peuvent pas être inversées. Ils sont déterministes et produisent la même production pour une entrée donnée. Toute modification de l’entrée produirait une sortie complètement différente lorsqu’elle serait à nouveau hachée.
• À l’aide de la cryptographie à clé publique, des signatures numériques sont possibles. Il permet de vérifier l’authenticité de la personne/entité qui a signé. Étant donné que la clé privée est gardée confidentielle, il n’est pas possible de forger une signature avec l’identité de quelqu’un d’autre. En outre, si quelqu’un a signé un document ou une transaction, il ne peut plus nier qu’il ne l’a pas fait.
• En utilisant des principes théorétiques de jeu et des pratiques exemplaires, des systèmes robustes peuvent être conçus qui peuvent soutenir dans la plupart des situations étranges. Les systèmes qui peuvent faire face au problème des généraux byzantins doivent être manipulés correctement. Notre approche de toute conception de système devrait être telle que les participants jouent selon les règles pour obtenir le gain maximum ; s’écarter du protocole ne devrait pas vraiment leur être bénéfique.
• La structure de données blockchain, en utilisant les hachages cryptographiques, fournit une chaîne de blocs résistante à la falsification. L’utilisation des arbres de Merkle facilite et accélère la vérification des transactions.

Avec tous ces concepts à l’esprit, pensons maintenant à une véritable mise en œuvre de la blockchain. Quels problèmes pouvez-vous penser qu’il faut aborder pour qu’un système aussi décentralisé fonctionne correctement ?

Eh bien, il y a beaucoup d’entre eux ; certains seraient génériques à la plupart des cas d’utilisation de la blockchain et certains seraient spécifiques à quelques-uns. Discutons au moins de certains des scénarios qui doivent être abordés :

• Qui conserverait le registre distribué des transactions ? Est-ce que tous les participants devraient maintenir, ou seulement quelques-uns feraient ? Que diriez-vous des nœuds informatiques qui ne sont pas assez puissants pour traiter les transactions ou qui n’ont pas assez d’espace de stockage pour s’adapter à toute l’histoire des transactions ?
• Comment est-il possible de maintenir un seul état cohérent du grand livre distribué ? Latence du réseau, perte de paquets, les tentatives de piratage délibérées, etc. sont inévitables. Comment le système survivrait-il à tout cela ?
• Qui validerait ou invaliderait les transactions ? Est-ce que seuls quelques nœuds autorisés valideraient, ou tous les nœuds ensemble parviendrait à un consensus ? Que se passe-t-il si certains nœuds ne sont pas disponibles à un moment donné ?
• Que se passe-t-il si certains nœuds informatiques veulent délibérément renverser le système ou essayer de rejeter certaines transactions ?
• Comment amélioreriez-vous le système lorsqu’il n’y a pas d’entité centralisée pour en assumer la responsabilité ? Dans un réseau décentralisé, que se passe-t-il si quelques nœuds informatiques se mettent à niveau et que les autres ne le font pas ?

Il y a en fait beaucoup plus de préoccupations qui doivent être abordées en dehors de ceux qui viennent d’être mentionnés. Pour l’instant, nous allons vous laisser avec ces pensées, mais la plupart de ces questions devraient être clarifiées d’ici la fin de ce chapitre.

Commençons par quelques éléments de base d’un système blockchain qui peut être nécessaire pour concevoir toute solution décentralisée.

Propriétés des solutions Blockchain

Jusqu’à présent, nous n’avons appris que les aspects techniques des solutions blockchain pour comprendre comment les blockchains pouvaient fonctionner. Dans cette section, nous allons apprendre quelques-unes des propriétés souhaitées des blockchains.

Immuabilité

C’est la propriété la plus désirée pour maintenir l’atomicité des transactions de blockchain. Une fois qu’une transaction est enregistrée, elle ne peut pas être modifiée. Si les transactions sont diffusées sur le réseau, alors presque tout le monde en a une copie. Avec le temps, quand de plus en plus de blocs sont ajoutés à la blockchain, l’immuabilité augmente et après un certain temps, elle devient complètement immuable. Pour modifier les données de tant de blocs dans une série ne soit pas réalisable, c’est parce qu’ils sont cryptographiquement sécurisés. Ainsi, toute transaction qui est enregistrée reste à jamais dans le système.

Résistant à la contrefaçon

Une solution décentralisée où les transactions sont publiques est sujette à différents types d’attaques. Les tentatives de faux sont les plus évidentes de toutes, surtout lorsque vous réalisez une transaction de quelque chose de valeur. Le hachage cryptographique et les signatures numériques peuvent être utilisés pour s’assurer que le système est résistant à la contrefaçon. Nous avons déjà appris qu’il est informatiquement impossible d’imiter la signature de quelqu’un d’autre. Si vous effectuez une transaction et signez un hachage de celle-ci, personne ne peut modifier la transaction plus tard et dire que vous avez signé une transaction différente. En outre, vous ne pouvez pas plus tard prétendre que vous n’avez jamais fait la transaction, parce que c’est vous qui l’avez signée.

Démocratique

Tout système décentralisé peer-to-peer devrait être démocratique par sa conception (peut ne pas être entièrement applicable à la blockchain privée, que nous allons ranger pour plus tard). Il ne devrait pas y avoir d’entité dans le système qui soit plus puissante que les autres. Chaque participant doit avoir des droits égaux dans n’importe quelle situation, et les décisions sont prises lorsque la majorité parvient à un consensus.

Résistant aux doubles dépenses

Les attaques à double dépense sont assez fréquentes dans les transactions monétaires et non monétaires. Dans un paramètre crypto-monnaie, une tentative de double dépense est lorsque vous essayez de dépenser le même montant à plusieurs personnes. Exemple : Vous avez 100 € dans votre compte et vous payez 90 € à deux parties ou plus est un prototype de double dépense. C’est un peu différent quand il s’agit de crypto-monnaie comme Bitcoin où il n’y a aucune notion de solde de clôture. L’entrée à une transaction (lorsque vous payez à quelqu’un) est la sortie d’une autre transaction où vous avez reçu au moins le montant que vous payez par le biais de cette transaction. Supposons que Bob a reçu 10 € d’Alice il y a quelque temps dans une transaction. Aujourd’hui, si Bob veut payer Charlie 8 €, alors la transaction dans laquelle il a reçu 10 € d’Alice serait l’entrée pour effectuer des transactions avec Charlie. Ainsi, Bob ne peut pas utiliser la même entrée (Alice lui a versé 10 €) plusieurs fois pour payer à d’autres personnes et double-dépenser. Juste pour vous donner un exemple différent : si quelqu’un possède des terres et vend le même morceau de terre à deux personnes.

Dans un système centralisé, il est assez facile d’empêcher les doubles dépenses parce que l’autorité centrale est au courant de toutes les transactions. Une solution blockchain devrait également être à l’abri de telles attaques à double dépense. Bien que la cryptographie assure l’authenticité d’une transaction, elle ne peut pas aider à empêcher les doubles dépenses. Parce que, techniquement, une transaction normale et une transaction à double dépense sont authentiques. Ainsi, la seule façon possible d’éviter les doubles dépenses est d’être au courant de toutes les transactions. Si nous sommes au courant de toutes les transactions qui se sont produites dans le passé, nous pouvons déterminer si une transaction est une tentative de double dépense. Ainsi, les nœuds qui valideraient les transactions devraient certainement être accessibles à l’ensemble des données de la blockchain depuis le bloc de genèse.

État cohérent du ledger

Les propriétés que nous venons de discuter garantissent la cohérence du grand livre partout, dans une certaine mesure. Imaginez une situation où certains nœuds veulent délibérément qu’une transaction ne passe pas et soit rejetée. Ou si en quelque sorte, certains nœuds ne sont pas synchronisés avec le grand livre et ne sont donc pas conscients de quelques transactions qui ont eu lieu alors qu’ils étaient hors ligne, puis pour eux la transaction peut sembler frauduleuse. Alors, assurer un consensus entre les participants est quelque chose qui doit être manipulé très soigneusement. Souvenez-vous du problème des généraux byzantins. Le bon type de consensus adapté à une situation donnée joue le rôle le plus important pour assurer stabilité d’une solution décentralisée. Nous apprendrons différents consensus mécanismes plus loin dans l’article.

Résiliente

Le réseau doit être suffisamment résistant pour résister à des défaillances temporaires des nœuds, à l’indisponibilité de certains nœuds informatiques à certains moments, à la latence du réseau et aux pertes de paquets, etc.

Vérifiables

Une blockchain est une chaîne de blocs qui sont reliés entre eux par des hachages. Étant donné que les blocs de transaction sont reliés jusqu’au bloc de genèse, l’auditabilité existe déjà et nous devons nous assurer qu’elle ne se casse pas à tout prix. En outre, si l’on veut vérifier si une transaction a eu lieu dans le passé, alors une telle vérification devrait être plus rapide.

Blockchain Transactions

Quand on parle de blockchain, on parle d’une blockchain de transactions, non ? Donc, il commence à partir d’une transaction, puis la transaction passe par une série d’étapes et réside finalement dans la blockchain. Étant donné que la blockchain est un phénomène peer-to-peer, si vous avez affaire à un cas d’utilisation qui a beaucoup de transactions qui ont lieu chaque seconde, vous ne voudrez peut-être pas inonder l’ensemble du réseau avec toutes les transactions. Évidemment, lorsqu’une personne ou une entité effectue une transaction, elle n’a qu’à la diffuser sur l’ensemble du réseau. Une fois que cela se produit, il doit être validé par plusieurs nœuds. Lors de la validation, il doit à nouveau être diffusé à l’ensemble du réseau pour la transaction d’être inclus dans la blockchain. Maintenant, pourquoi pas une chaîne de transactions au lieu d’une blockchain ? Il peut être logique dans une certaine mesure si votre analyse de rentabilisation n’implique pas beaucoup de transactions. Cependant, s’il y a un grand nombre de transactions chaque seconde, puis les hachages au niveau de la transaction, en gardant une trace de celui-ci, et la diffusion que le réseau peut rendre le système instable. Vous pouvez vouloir qu’un certain nombre de transactions soient regroupées dans un bloc et diffusent ce bloc. La diffusion de transactions individuelles peut devenir une affaire coûteuse. Une autre bonne raison pour une blockchain au lieu d’une chaîne de transactions est d’empêcher la Sybil Attack. Dans le chapitre 3, vous apprendrez plus en détail comment l’algorithme de minage PoW est utilisé et un nœud est choisi au hasard qui pourrait proposer un bloc. Si ce n’était pas le cas, les gens pourraient créer des répliques de leur propre nœud pour renverser le système.

Dans sa forme la plus simplifiée, les transactions blockchain passent par les étapes suivantes pour entrer dans la blockchain:

• Chaque nouvelle transaction est diffusée sur le réseau de sorte que tous les nœuds informatiques sont conscients de ce fait au moment où il a eu lieu (pour s’assurer que le système est résistant à la double dépense).
• Les transactions peuvent être validées par les nœuds à accepter ou à rejeter en vérifiant l’authenticité.
• Les nœuds peuvent ensuite regrouper plusieurs transactions en blocs à partager avec les autres nœuds du réseau.
• Voici la situation difficile. Qui proposerait le bloc de transactions qu’ils ont regroupés individuellement ? D’une manière générale, la génération de nouveaux blocs devrait être contrôlée, mais pas de manière centralisée, et le mécanisme devrait être tel que chaque nœud est prioritaire. Chaque nœud en accord sur un bloc est appelé le consensus, mais il existe différents algorithmes pour atteindre le même objectif, en fonction de votre cas d’utilisation. Nous discuterons des différents mécanismes de consensus dans la section suivante.
• Bien qu’il n’y ait aucune notion d’un temps global en raison de la latence du réseau, des pertes de paquets, et des emplacements géographiques, un tel système fonctionne toujours parce que les blocs sont ajoutés l’un après l’autre dans un ordre. Ainsi, nous pouvons considérer que les blocs sont horodatés dans l’ordre où ils arrivent et sont ajoutés dans la blockchain.
• Une fois que les nœuds dans le réseau acceptent unanimement un bloc, alors ce bloc pénètre dans la blockchain et il inclut le hachage du bloc qui a été créé juste avant lui. Cela prolonge donc la blockchain d’un bloc.

Nous avons déjà discuté de la structure de données blockchain et les arbres Merkle, donc nous comprenons leur valeur maintenant. Se rappeler que lorsqu’un nœud souhaite valider une transaction, il peut le faire plus efficacement par le chemin Merkle. Les autres nœuds du réseau n’ont pas à partager le bloc complet de données pour justifier la preuve de l’appartenance à une transaction dans un bloc. Techniquement parlant, les structures de données économes en mémoire et adaptées à l’ordinateur telles que les « filtres Bloom » sont largement utilisées dans de tels scénarios pour tester l’adhésion.

En outre, notez que pour qu’un nœud puisse valider une transaction, il devrait idéalement avoir localement l’ensemble des données blockchain (transactions avec leurs métadonnées). Vous devez sélectionner un mécanisme de stockage efficace que les nœuds adopteront en fonction de votre cas d’utilisation.

Mécanismes de consensus distribués

Lorsque les nœuds sont au courant de toute l’histoire des transactions en ayant une copie locale des données complètes de la blockchain pour éviter les doubles dépenses, et qu’ils peuvent vérifier l’authenticité d’une transaction par le biais de signatures numériques, à quoi sert le consensus ? Imaginez la présence d’un ou de plusieurs nœuds malveillants. Ne peuvent-ils pas dire qu’une transaction non valide est valide, ou vice versa ? Souvenons-nous du problème des généraux byzantins, qui est le plus susceptible de se produire dans de nombreux systèmes décentralisés. Pour surmonter ces problèmes, nous avons besoin d’un mécanisme de consensus approprié en place.

Jusqu’à présent, dans notre discussion, la seule chose qui n’est pas encore claire est de savoir qui propose le bloc. Évidemment, tous les nœuds ne doivent pas proposer un bloc au reste des nœuds en même temps parce que cela va créer un désordre. D’autre part, si cela avait été le cas avec des transactions sans les regrouper en blocs, on pourrait faire valoir que si chaque transaction est diffusée à l’ensemble du réseau et chaque nœud dans le réseau jette un vote sur ces transactions individuelles, il ne ferait que compliquer le système et conduire à de mauvaises performances.

Ainsi, le regroupement des transactions en blocs est important pour des raisons évidentes et un consensus est nécessaire sur une base bloc par bloc. La meilleure stratégie pour ce problème est qu’un seul bloc devrait proposer un bloc à la fois et le reste des nœuds devraient valider les transactions dans le bloc et les ajouter à leurs blockchains si les transactions sont valides. Nous savons que chaque nœud conserve sa propre copie du registre et qu’il n’y a pas de source centralisée à synchroniser. Donc, si un nœud propose un bloc et le reste des nœuds est d’accord avec elle, alors tous ces nœuds ajouteront ce bloc à leurs blockchains respectives. Dans une telle conception, vous préféreriez qu’il y ait au moins quelques minutes d’écart dans la création de bloc et il ne devrait pas être le cas où plusieurs blocs arrivent en même temps. Maintenant, la question est : qui pourrait être ce nœud chanceux de proposer un bloc ? C’est la partie la plus délicate et peut conduire à un consensus approprié ; nous discuterons de cet aspect dans le cadre de différents mécanismes de consensus.

Ces mécanismes de consensus proviennent en fait de la théorie des jeux. Votre système doit être conçu de telle sorte que les nœuds obtiennent le plus d’avantages s’ils jouent selon les règles. Un des aspects pour s’assurer que les nœuds se comportent honnêtement est de récompenser pour le comportement honnête et punir pour les activités frauduleuses. Cependant, il y a un hic ici. Dans une blockchain publique comme Bitcoin, on peut avoir de nombreuses identités publiques différentes et elles sont tout à fait anonymes. Il devient vraiment difficile de punir ces identités parce qu’elles ont le choix d’éviter cette punition en créant de nouvelles identités pour elles-mêmes. D’autre part, les récompenser fonctionne très bien, parce que même si quelqu’un a plusieurs identités, ils peuvent heureusement récolter les récompenses qui leur sont données. Donc, cela dépend de votre analyse de rentabilisation : si les identités sont anonymes, puis les punir peut ne pas fonctionner, mais peut bien fonctionner si les identités ne sont pas anonymes. Vous pouvez considérer cet aspect de récompense/punition en dépit d’avoir un grand mécanisme pour sélectionner un nœud qui proposerait le prochain bloc. C’est parce que vous ne sauriez jamais à l’avance si le nœud sélectionné est un nœud malveillant ou honnête. Gardez à l’esprit le terme de minage que nous utiliserons assez souvent, et cela signifierait générer de nouveaux blocs.

L’objectif du consensus est également de s’assurer que le réseau est suffisamment robuste pour soutenir divers types d’attaques. Indépendamment des types d’algorithmes de consensus que l’on peut choisir en fonction du cas d’utilisation, il doit tomber dans le moule de consensus tolérant à la faute byzantine pour être en mesure d’être accepté. Apprenons maintenant quelques-uns des mécanismes de consensus relatifs aux scénarios de blockchain que nous pourrions utiliser dans différentes situations.

Preuve de travail – POW

Le mécanisme de consensus PoW existe depuis longtemps. Cependant, la façon dont il a été utilisé dans Bitcoin avec d’autres concepts l’a rendu encore plus populaire. Nous discuterons de ce mécanisme de consensus à son niveau de base et examinerons comment il est mis en œuvre dans Bitcoin au chapitre 3.

L’idée derrière l’algorithme PoW est que certains travaux sont effectués pour un bloc de transactions avant qu’il ne soit proposé à l’ensemble du réseau. Un PoW est en fait un morceau de données qui est difficile à produire en termes de calcul et de temps, mais facile à vérifier. L’un des anciens usages de PoW était de prévenir les spams par e-mail. Si une certaine quantité de travail doit être faite avant que l’on puisse envoyer un e-mail, alors spammer beaucoup de gens aurait besoin de beaucoup de puissance de calcul. Cela peut aider à prévenir les spams par e-mail. De même dans la blockchain, si une certaine quantité de travail à forte intensité de calcul doit être effectuée avant de produire un bloc, alors il peut aider de deux façons : l’un est qu’il va certainement prendre un certain temps et le second est, si un nœud tente d’injecter une transaction frauduleuse dans un bloc, alors le rejet de ce bloc par le reste des nœuds sera très coûteux pour celui qui propose le bloc. C’est parce que le calcul effectué pour obtenir le PoW n’aura aucune valeur.

Il suffit de penser à proposer un bloc sans beaucoup d’efforts vs faire un peu de travail acharné pour être en mesure de proposer un bloc. Si c’était avec presque aucun effort, alors proposer un nœud avec une transaction frauduleuse et se faire rejeter n’aurait pas été une grande préoccupation. Les gens peuvent juste continuer à proposer de tels blocs avec l’espoir que l’on peut passer à travers et le faire à la blockchain parfois. Au contraire, faire un travail acharné pour proposer un bloc empêche un nœud d’injecter une transaction frauduleuse d’une manière subtile.

De plus, la difficulté du travail doit être ajustable afin de contrôler la vitesse à laquelle les blocs peuvent être générés. Vous devez penser, si nous parlons d’un travail qui nécessite un certain calcul et du temps, quel genre de travail doit-il être ? C’est un travail très simple mais délicat. Un exemple serait utile ici. Imaginez un problème où vous devez trouver un nombre qui, si vous hachiez, la sortie hachée commencerait par l’alphabet « a ». Comment feriez-vous ? Nous avons appris les fonctions de hachage et savons qu’il n’y a pas de raccourcis. Donc, vous deviez simplement deviner (peut-être prendre n’importe quel nombre et continuer à l’incrémenter d’un) les chiffres et continuer à les hacher pour voir si cela correspond au résultat. Si le niveau de difficulté doit être augmenté, on peut dire qu’il commence par trois « a » consécutifs. De toute évidence, trouver une solution pour quelque chose comme «axxxxxxx» est plus facile à trouver que «aaaxxxxx» car ce dernier est plus contraint.

Dans l’exemple qui vient d’être donné, si plusieurs nœuds différents travaillent à résoudre un tel puzzle de calcul, alors vous ne saurez jamais quel nœud le résoudrait en premier. Cela peut être utilisé pour sélectionner un nœud aléatoire (cette fois, il est vraiment aléatoire parce qu’il n’y a pas d’algorithme derrière elle) qui résout le puzzle et propose le bloc. Il est extrêmement important de noter qu’en cas de blockchains publiques, les nœuds qui investissent leurs ressources informatiques doivent être récompensés pour un comportement honnête, sinon il serait difficile de soutenir un tel système.

Preuve d’enjeu – POS

L’algorithme Proof of Stake (PoS) est un autre algorithme de consensus qui est très populaire pour le consensus distribué. Cependant, ce qui est délicat à ce sujet, c’est qu’il ne s’agit pas de l’exploitation minière, mais de la validation de blocs de transactions. Il n’y a pas de récompenses minières dues à la génération de nouvelles pièces, il n’y a que des frais de transaction pour les mineurs (plus précisément les validateurs, mais nous allons continuer à utiliser des «mineurs» de sorte qu’il devient plus facile à expliquer).

Dans les systèmes PoS, les validateurs doivent cautionner leur participation (hypothèque le montant de la crypto-monnaie qu’ils souhaite garder en jeu) pour être en mesure de participer à la validation des transactions. La probabilité qu’un validateur produise un bloc est proportionnelle à son enjeu; plus le montant en jeu est élevé, plus ils ont la chance de valider un nouveau bloc de transactions. Un mineur n’a qu’à prouver qu’il possède un certain pourcentage de toutes les pièces disponibles à un certain moment dans un système monétaire donné. Par exemple, si un mineur possède 2 % de l’ensemble d’Ether (ETH) dans le réseau Ethereum, il serait en mesure d’exploiter 2 % de toutes les transactions à travers Ethereum. En conséquence, qui obtient de créer le nouveau bloc de transaction est décidé, et il varie en fonction de l’algorithme PoS que vous utilisez. Oui, il existe des variantes de l’algorithme PoS tels que PoS naïf, PoS délégué, PoS à chaîne, PoS de style BFT, et Casper PoS, pour n’en nommer que quelques-uns. Le PoS délégué (DPOS) est utilisé par Bitshares et Casper PoS est en cours de développement pour être utilisé dans l’Ethereum.

Depuis que le créateur d’un bloc dans un système PoS est déterministe (basé sur le montant en jeu), il fonctionne beaucoup plus vite par rapport aux systèmes PoW. En outre, comme il n’y a pas de récompenses en bloc et juste des frais de transaction, toutes les monnaies numériques doivent être créées au début et leur montant total est fixé tout au long.

Les systèmes PoS peuvent fournir une meilleure protection contre les attaques malveillantes, car l’exécution d’une attaque risquerait la totalité du montant en jeu. En outre, comme il ne nécessite pas de brûler beaucoup d’électricité et de consommer des cycles CPU, il obtient la priorité sur les systèmes PoW le cas échéant.

PBFT (en anglais)

PBFT est l’acronyme de l’algorithme Practical Byzantine Fault Tollerance, l’un des nombreux algorithmes de consensus que l’on peut considérer pour leur cas d’utilisation de la blockchain. Parmi tant d’initiatives de blockchain, Hyperledger, Stellar et Ripple sont ceux qui utilisent le consensus PBFT.

PBFT est également un algorithme qui n’est pas utilisé pour générer des récompenses de minage, similaire aux algorithmes PoS. Cependant, les aspects techniques de leurs implémentations respectives sont différents. Le travail interne de PBFT est au-delà de la portée de l’article, mais à un niveau élevé, les demandes sont diffusées à tous les nœuds participants qui ont leurs propres répliques ou des états internes. Lorsque les nœuds reçoivent une demande, ils effectuent le calcul en fonction de leurs états internes. Le résultat du calcul est ensuite partagé avec tous les autres nœuds du système. Ainsi, chaque nœud est conscient de ce que les autres nœuds ont calculé. Compte tenu de leurs propres résultats de calcul ainsi que ceux reçus des nœuds actifs, ils prennent une décision et s’engagent à une valeur finale, qui est à nouveau partagée entre les nœuds. À ce moment, chaque nœud est au courant de la décision finale de tous les autres nœuds. Ensuite, ils répondent tous par leurs décisions finales et, sur la base de la majorité, le consensus final est atteint. C’est ce que montre la figure 2-24.

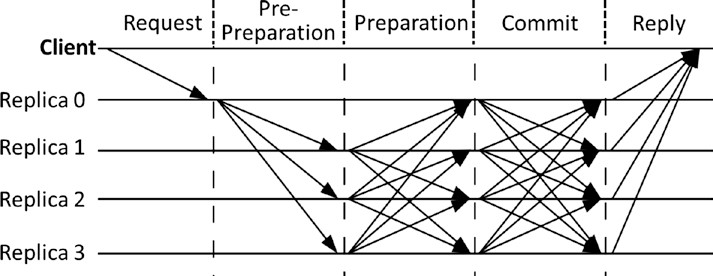
Figure 2-24. Approche consensuelle du PBFT

PBFT peut être efficace par rapport à d’autres algorithmes de consensus, en fonction de l’effort requis. Cependant, l’anonymat dans le système peut être compromis en raison de la façon dont cet algorithme est conçu. C’est l’un des algorithmes les plus utilisés pour le consensus, même dans les environnements non-blockchain.

Blockchain Applications

Alors que nous avons examiné les écrous et les boulons de la blockchain tout au long de ce chapitre, il est également important que nous regardions comment il est utilisé dans la construction de solutions blockchain. Il y a des applications en cours de construction qui traitent blockchain comme une base de données backend derrière un serveur web, et il y a des applications qui sont complètement décentralisés sans serveur centralisé. Bitcoin blockchain, par exemple, est une application blockchain où il n’y a pas de serveur pour envoyer une demande ! Chaque transaction est diffusée sur l’ensemble du réseau. Cependant, il est possible qu’une application web soit construite et hébergée dans un serveur Web centralisé, ce qui rend les mises à jour de la blockchain Bitcoin plus agile. Jetez un coup d’œil à la figure 2-25 où un nœud Bitcoin diffuse les transactions aux nœuds accessibles à un moment donné.

Figure 2-25. Nœuds blockchain Bitcoin

Du point de vue des applications logicielles, chaque nœud est autosuffisant et conserve ses propres copies de la base de données blockchain. Considérant la blockchain Bitcoin comme une référence, les applications blockchain sans serveurs centralisés semblent être les applications décentralisées les plus pures et la plupart d’entre elles relèvent de la catégorie « blockchain publique ». Habituellement, pour ces blockchains publiques, l’utilisation des ressources des fournisseurs de services cloud tels que Microsoft Azure, IBM Bluemix, etc ne sont pas encore très populaires. Pour la plupart des blockchains privées, cependant, les fournisseurs de services cloud ont commencé à gagner en popularité. Pour vous donner une analogie, il pourrait y avoir une ou plusieurs applications web pour différents départements ou acteurs, tous ayant leurs propres backends Blockchain et encore les blockchains sont en phase les uns avec les autres. Dans un tel contexte, bien que la décentralisation technique soit réalisée, politiquement elle pourrait encore être centralisée. Même si le contrôle ou la gouvernance sont appliqués, le système est toujours en mesure de maintenir la transparence et la confiance en raison de l’accessibilité à une source unique de vérité. Jetez un œil à la figure 2-26, qui peut ressembler à la plupart des POP blockchain ou des applications en cours de construction sur blockchain où les blockchains sont hébergés par un fournisseur de services cloud en utilisant leur blockchain-as-a-Service (BaaS).

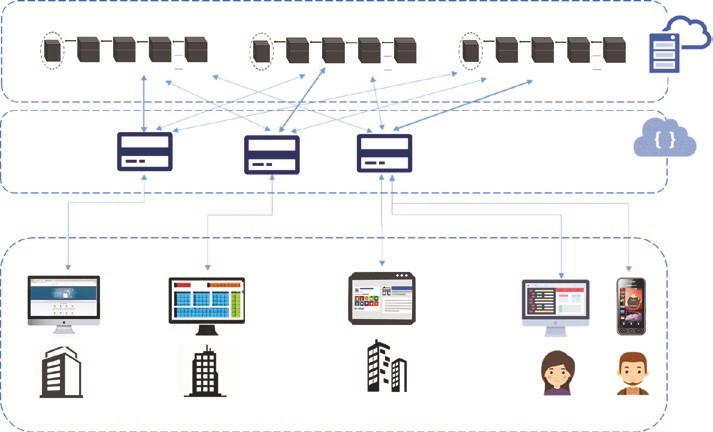
Genèse

Bloc

Bloc précédent

Bloc-1

Bloc-2

Bloc-3

Bloc-4

Bloc-1265

Transactions

Bloc précédent

Transactions

Bloc précédent

Transactions

Bloc précédent

Transactions

Bloc précédent

Transactions

Bloc précédent

Transactions

Bloc précédent

Transactions

Bloc précédent

Transactions

Bloc précédent

Transactions

Bloc précédent

Transactions

Bloc précédent

Transactions

Bloc précédent

Transactions

Genèse

Bloc

Bloc-1

Bloc-2

Bloc-3

Bloc-4

Bloc-1265

Genèse

Bloc

Bloc-1

Bloc-2

Bloc-3

Bloc-4

Bloc-1265

Blockchain Blockchain

Département Un

Département B

Département C.

Serveurs Web

L’application est hébergé ici

Acteurs dans un système Blockchain Blockchain

Figure 2-26. Système blockchain alimenté par le cloud

Il n’est peut-être pas nécessaire que tous les départements aient leur propre application Web. Une application web peut traiter les demandes de plusieurs acteurs différents dans le système avec des mécanismes de contrôle d’accès approprié. Il pourrait être une bonne idée que tous les acteurs du système ont leurs propres copies de blockchain. Avoir une copie locale de la blockchain contribue non seulement à maintenir la transparence dans le système, mais peut également aider à générer des informations axées sur les données avec un accès facile aux données tout le temps. Les différentes « blockchains » maintenues par les différents acteurs du système sont cohérentes par la conception, grâce à des algorithmes consensuels tels que PoW, PoS, etc. La plupart des blockchains privées préfèrent tout algorithme de consensus autre que PoW pour atténuer la consommation de ressources lourdes, et économiser l’électricité et la puissance de calcul autant que possible. Le mécanisme de consensus PoS est assez courant lorsqu’il s’agit de blockchains privées ou de consortiums. Étant donné que la blockchain perturbe de nombreux aspects des entreprises, et qu’il n’y avait pas de meilleur moyen de permettre la transparence entre eux, la création d’une solution blockchain dans le cloud avec un modèle « payer comme vous utilisez » prend de l’ampleur. Les services Cloud aident les entreprises à faire un bond en avant dans leur parcours de transformation numérique compatible avec la blockchain avec des investissements initiaux minimes.

Des applications décentralisées (DApps) sont également construites sur les réseaux de blockchain Ethereum. Ces applications pourraient être autorisées sur Ethereum privé ou pourraient être sans autorisation sur un réseau public Ethereum. En outre, ces applications pourraient être pour différents cas d’utilisation sur le même réseau public Ethereum. Bien que nous allons couvrir les détails spécifiques d’Ethereum dans un chapitre prochain, il suffit de regarder la figure 2-27 pour avoir une compréhension de haut niveau de la façon dont ces applications fonctionnent.

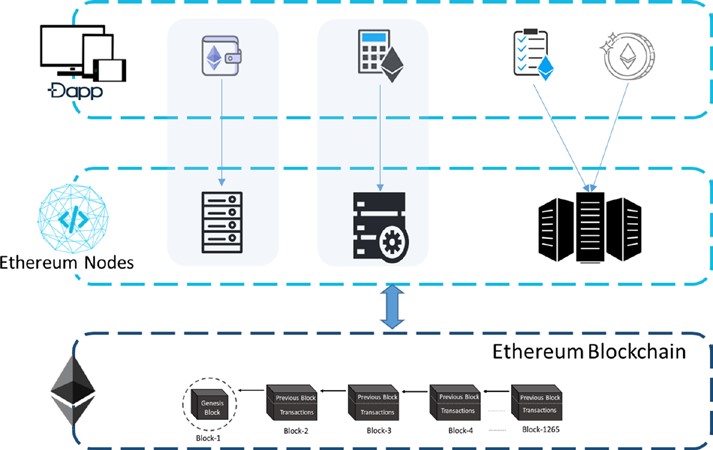
Figure 2-27. DApps sur le réseau Ethereum

Comme nous l’avons déjà vu dans les sections précédentes, le développement d’applications blockchain n’est limité que par votre imagination. Des applications natives de la blockchain pures pourraient être construites. Des applications qui traitent la blockchain comme un simple backend sont également en cours de construction, et il existe des applications hybrides qui sont également en cours de construction qui utilisent les applications héritées et utilise la blockchain à des fins spécifiques. Jusqu’à présent, l’évolutivité de la blockchain est l’une des plus grandes préoccupations. Bien que l’évolutivité elle-même est dans la recherche, nous allons apprendre quelques-unes des techniques d’évolutivité.

Mise à l’échelle blockchain

Nous avons examiné la blockchain d’un point de vue historique et comment elle s’avère être l’une des technologies les plus perturbatrices du monde d’aujourd’hui.

De par leur conception, les blockchains sont difficiles à mettre à l’échelle et constituent donc un domaine de recherche dans le milieu universitaire et pour certaines entreprises axées sur l’innovation. Si vous regardez l’adoption Bitcoin, il n’est pas utilisé pour remplacer les monnaies fiduciaires en raison des défis inhérents à l’évolutivité. Vous ne pouvez pas acheter un café en utilisant Bitcoin et attendre une heure pour que la transaction se règle. Ainsi, Bitcoin est utilisé comme une classe d’actifs pour les investisseurs. Un réseau blockchain Bitcoin n’est pas en mesure d’accueillir autant de transactions que celle de Visa ou MasterCard, actuellement.

Résoudre les protocoles de consensus que nous avons étudiés jusqu’à présent, tels que PoW de Bitcoins ou Ethereum, ou PoS et d’autres consensus BFT de certaines autres spécificités blockchain telles que Multichain, Hyperledger, Ripple, ou Tendermint. Tous ces algorithmes consensuels sont la tolérance à la faute byzantine. Par sa conception, chaque nœud (au moins les nœuds complets) d’un réseau blockchain conserve leur propre copie de l’ensemble de la blockchain, valide toutes les transactions et les blocs, répond aux demandes d’autres nœuds du réseau, etc. pour parvenir à la décentralisation, qui est de ce fait un goulet d’étranglement pour l’évolutivité. Regardez l’ironie ici, nous ajoutons plus de serveurs dans un système centralisé pour l’évolutivité, mais la même chose ne s’applique pas dans un système décentralisé parce qu’avec plus de nombre de nœuds, la latence ne fait qu’augmenter. Alors que le niveau de décentralisation pourrait augmenter avec un plus grand nombre de nœuds dans un réseau décentralisé, le nombre de transactions dans le réseau augmente également, ce qui conduit à une augmentation des besoins en ressources informatiques et de stockage. Gardez à l’esprit que cette situation est plus applicable sur les blockchains publiques et moins pour les blockchains privées. Les blockchains privées pourraient facilement évoluer par rapport aux entités publiques parce que les entités de contrôle peuvent définir des spécifications de nœud avec une puissance de calcul élevée et plus de bande passante. En outre, il pourrait y avoir certaines tâches déchargées de la blockchain et décloisonner le calcul hors de la chaîne, ce qui peut aider le système à bien évoluer.

Dans ce chapitre, nous allons apprendre quelques-unes des techniques de mise à l’échelle génériques, et discuter des techniques de mise à l’échelle bitcoin et Ethereum-spécifiques dans leurs chapitres respectifs. Gardons à l’esprit que toutes les techniques de mise à l’échelle peuvent ne pas s’appliquer à toutes sortes de spécificités blockchain ou des cas d’utilisation. La meilleure façon est de comprendre les techniques et d’utiliser les meilleurs possibles dans une situation donnée.

Calcul hors chaîne

Le calcul hors chaîne est l’une des techniques les plus prometteuses pour mettre à l’échelle les solutions blockchain. L’idée est de limiter l’utilisation de la blockchain et de faire le gros du travail en dehors de celle-ci et de stocker uniquement les résultats sur la blockchain. Gardons à l’esprit qu’il n’existe pas de définition standard de la façon dont le calcul hors chaîne devrait se produire. Elle dépend fortement de la situation et des gens qui essaient d’y remédier. En outre, différentes spécificités blockchain peuvent nécessiter des approches différentes pour le calcul hors chaîne. À un niveau élevé, c’est comme une autre couche au-dessus de la blockchain qui fait un travail lourd et exigeant en calcul et utilise judicieusement la blockchain. Évidemment, vous ne pouvez pas être en mesure de conserver toutes les caractéristiques de la blockchain en faisant des calculs hors chaîne, mais il est également vrai que vous ne pouvez pas avoir besoin de blockchain pour toutes sortes d’exigences informatiques et ne l’utiliser uniquement pour des points spécifiques de gestion de la complexité.

Les calculs hors chaîne pourraient être sur une chaîne latérale, pourraient être distribués parmi un groupe aléatoire de nœuds, ou pourraient également être centralisés. Les chaînes latérales sont indépendantes de la blockchain principale. Cela permet non seulement de bien dimensionner la blockchain, mais également d’isoler les dommages de la chaîne latérale et d’empêcher la blockchain principale de tout dommage causé par une chaîne latérale. Un tel exemple de sidechain est le «Lightning Network» pour Bitcoins qui devrait aider à une exécution plus rapide des transactions avec des frais minimes; qui prendra également en charge les micropaiements. Un autre exemple de chaîne secondaire pour Bitcoins est «Zerocash», dont l’objectif principal n’est pas vraiment l’évolutivité, mais la confidentialité. Si vous utilisez Zerocash pour les transactions Bitcoin, vous ne pouvez pas être suivi et votre confidentialité est préservée. Nous limiterons notre discussion aux techniques d’évolutivité génériques et n’entrerons pas dans une discussion détaillée de l’évolutivité Bitcoin dans cet article.

Une question évidente qui pourrait se poser à l’heure actuelle est de savoir comment les gens vérifieraient l’authenticité des transactions si elles sont envoyées hors chaîne. Tout d’abord, pour créer une transaction valide, vous n’avez pas besoin d’une blockchain. Nous avons appris dans la section “Cryptographie” dans ce chapitre sur la cryptographie de clé asymétrique qui est utilisée par le système blockchain. Pour effectuer une transaction, vous devez être le propriétaire d’une clé privée afin de pouvoir signer la transaction. Une fois que la transaction est créée, il y a des avantages quand elle entre dans la blockchain. La Double-dépenses n’est pas possible avec la blockchain Bitcoin, et il y a d’autres avantages, aussi. Pour l’instant, le seul objectif est de vous faire prendre en compte avec le fait que vous pouvez créer une transaction tant que vous possédez la clé privée de votre compte.

Les blockchains Bitcoin sont une blockchain sans état, en ce sens qu’elles ne maintiennent pas l’état d’un compte. Tout dans la blockchain Bitcoin est présent sous la forme d’une transaction. Pour être en mesure de faire une transaction, vous devez consommer une transaction précédente et il n’y a aucune notion de « solde de clôture » pour un compte, en tant que tel. Au contraire, la blockchain Ethereum est une blockchain « à états » ! Les blocs de la blockchain Ethereum contiennent des informations en ce qui concerne l’état de l’ensemble du bloc où le solde du compte est également une partie. L’information d’état prend beaucoup de place lorsque chaque nœud du réseau le maintien. Cette situation est valable pour d’autres blockchains aussi bien.

Prenons un exemple pour mieux comprendre cela. Alice et Bob sont deux parties ayant plusieurs transactions entre eux. Disons qu’ils ont généralement 50 transactions monétaires en un mois. Dans une blockchain « à états », toutes ces transactions individuelles auraient leurs informations d’état, et qui seront maintenues par tous les nœuds. Pour relever ce défi, le concept de « canaux d’État » est introduit. L’idée est de mettre à jour la blockchain avec le résultat final, par exemple, à la fin du mois ou quand un certain seuil de transaction est atteint, et non pas à chaque transaction.

Les canaux d’État sont essentiellement un canal de communication bidirectionnel entre les utilisateurs, les objets ou les services. Cela se fait avec une sécurité absolue en utilisant des techniques cryptographiques. Juste pour avoir un aperçu de la façon dont cela fonctionne, jetez un œil à la figure 2-28.

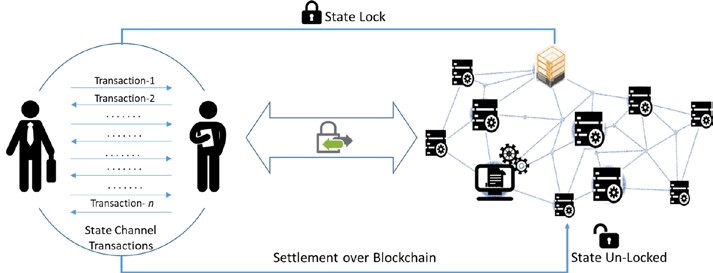
Figure 2-28. Chaînes d’État pour le calcul hors chaîne

Notez que les canaux d’État hors chaîne sont pour la plupart privés et confinés parmi un groupe de participants. Gardez à l’esprit que l’état de la blockchain pour les participants doit être verrouillé comme première étape. Soit il pourrait s’agir d’un système MultiSig ou d’un verrouillage intelligent basé sur un contrat. Après le verrouillage, les participants font des transactions entre eux qui sont sécurisées cryptographiquement. Toutes les transactions sont cryptographiques signées, ce qui les rend vérifiables et ces transactions ne sont pas immédiatement soumises à la blockchain. Comme nous l’avons vu, ces canaux d’État pourraient avoir une durée de vie prédéfinie, ou pourraient être liés au montant des transactions effectuées en volume/quantité ou à toute autre mesure quantifiable. Ainsi, le résultat final des transactions est réglé sur la blockchain et déverrouille l’état comme l’étape finale.

Les canaux d’État pourraient être mis en œuvre très différemment dans différents cas d’utilisation, et leurs implémentations sont en fait laissées aux développeurs. C’est certainement une voie à suivre et c’est l’un des éléments les plus critiques pour l’adoption généralisée des applications blockchain. Pour Bitcoin, le Lightning Network a été conçu pour le calcul hors chaîne et pour accélérer la transaction de paiement. De même, le “Raiden Network” a été conçu pour la blockchain Ethereum. Il existe de nombreux autres développements de ce type pour rendre les micropaiements plus rapides et plus réalisables sur les réseaux blockchain.

État de la Blockchain Sharding

Sharding est l’une des techniques d’évolutivité qui a été là pendant des siècles et a été un sujet plus recherché pour les bases de données. Les gens ont utilisé cette technique différemment dans différents cas d’utilisation pour relever des défis d’évolutivité spécifiques. Avant de comprendre comment il pourrait être utilisé dans la mise à l’échelle blockchain ainsi, nous allons d’abord comprendre ce que cela signifie.

La lecture/écriture de disque a toujours été un goulet d’étranglement lorsqu’il s’agit d’énormes jeux de données. Lorsque les données sont divisées sur plusieurs disques, la lecture/écriture peut être effectuée en parallèle et la latence diminue considérablement.

Cette technique est appelée sharding. Jetez un coup d’œil à la figure 2-29.

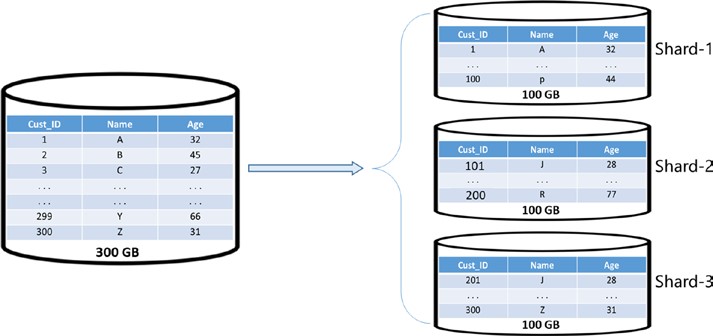
Figure 2-29. Exemple de sharding de base de données

Notez à la figure 2-29 comment le cloisonnement horizontal est effectué pour distribuer une table de base de données de 300 Go en trois éclats de 100 Go chacun et stockés sur des instances de serveur séparées. Le même concept s’applique également à la blockchain, où l’état global de la blockchain est divisé en différents éclats qui contiennent leurs propres sous-états. Eh bien, il n’est certainement pas aussi facile que de partitionner une base de données avec juste du partitionnement horizontal.

Alors, comment fonctionne vraiment le sharding dans le contexte de la blockchain ? L’idée est que les nœuds ne seront pas tenus de télécharger et de conserver une copie de l’ensemble de la blockchain. Au lieu de cela, ils téléchargeraient et conserveraient les portions (fragments) pertinentes pour eux. Ce faisant, ils ne peuvent traiter que les transactions pertinentes pour les données qu’ils stockent, et l’exécution parallèle des transactions est possible. Ainsi, lorsqu’une transaction se produit, elle est acheminée vers des nœuds spécifiques uniquement en fonction des fragments qu’ils affectent. Si vous le regardez sous un angle différent, tous les nœuds ne sont pas tenus de faire toutes sortes de calculs et de vérifications pour chaque transaction. Un mécanisme ou un protocole pourrait être défini pour la communication entre les fragments lorsque plusieurs fragments sont nécessaires pour traiter des transactions spécifiques. Veuillez garder à l’esprit que différentes chaînes de blocs peuvent avoir différentes variantes de partage.

Pour vous donner un exemple, vous pouvez choisir une technique de partitionnement spécifique pour une situation donnée. Un exemple pourrait être où les fragments doivent avoir plusieurs comptes uniques en eux. En d’autres termes, chaque compte unique est dans un fragment (plus applicable pour les blockchains de style Ethereum qui sont avec état), et il est très facile pour les comptes dans un fragment de traiter entre eux. De toute évidence, une extraction de niveau supplémentaire au niveau d’un fragment est nécessaire pour que le partitionnement fonctionne, et les nœuds ne peuvent conserver qu’un sous-ensemble des informations.

Résumé

Dans ce chapitre, nous avons plongé profondément dans les principes fondamentaux de la cryptographie, de la théorie des jeux et de l’ingénierie informatique. Les concepts appris vous aideraient à concevoir votre propre solution blockchain qui peut avoir des besoins spécifiques. Blockchain n’est certainement pas une solution miracle pour toutes sortes de problèmes. Cependant, pour ceux où la blockchain est nécessaire, il est très probable que différentes spécificités de solutions blockchain seraient nécessaires avec différentes constructions de conception.

Nous avons appris différentes techniques cryptographiques pour sécuriser les transactions et l’utilité des fonctions de hachage. Nous avons examiné comment la théorie des jeux pourrait être utilisée pour concevoir des solutions robustes. Nous avons également appris quelques-uns des principes fondamentaux de l’informatique tels que la structure des données blockchain et les arbres Merkle. Certains des concepts ont été supplées avec des extraits de code par exemple pour vous donner un bon départ sur vos affectations blockchain.

Dans le chapitre suivant, nous allons en apprendre davantage sur Bitcoin comme un cas d’utilisation blockchain, et comment exactement cela fonctionne.

CHAPITRE 3 Comment fonctionne Bitcoin

La technologie Blockchain fait fureur ces jours-ci, grâce à Bitcoin ! blockchain comme nous le savons c’est un cadeau de Bitcoin et son inventeur, Satoshi Nakamoto, au monde entier. Si vous vous demandez qui est Satoshi Nakamoto, c’est le nom utilisé par la personne inconnue ou les personnes qui sont à l’origine de Bitcoin. Nous vous suggérons de comprendre et d’apprécier la merveilleuse technologie derrière Bitcoin sans chercher l’inventeur. Apprendre les bases techniques de Bitcoin vous permettra de comprendre les autres applications blockchain qui sont là sur le marché.

Depuis Bitcoin a témoigné de la robustesse de la technologie blockchain depuis des années, les gens y croient maintenant et ont commencé à explorer d’autres façons possibles de l’utiliser. Dans le chapitre précédent, nous avons déjà eu l’apprentissage du niveau technique, mais la compréhension de Bitcoin peut vous donner le vrai goût de la blockchain. Vous pouvez considérer Bitcoin comme un cas d’utilisation de crypto-monnaie de la technologie blockchain. Ainsi, ce chapitre vous aidera non seulement à comprendre en particulier, mais vous donnera également une perspective de la façon dont différents cas d’utilisations peuvent être construits en utilisant la technologie blockchain, la façon dont Bitcoin est construit.

Nous couvrirons Bitcoin plus en détail tout au long de ce chapitre et, ce faisant, beaucoup de fondamentaux de la blockchain seront également clarifiés avec des idées plus pratiques. Si vous connaissez déjà les fondamentaux Bitcoin, vous pouvez sauter ce chapitre. Sinon, nous vous conseillons de suivre les concepts dans l’ordre présenté. Ce chapitre explique ce qu’est Bitcoin, comment il est conçu techniquement, et fournit une analyse de certaines forces et faiblesses inhérentes de Bitcoin.

L’histoire de l’argent

Vous êtes-vous déjà demandé ce qu’est l’argent et pourquoi il existe? L’argent est avant tout le moyen d’échange pour l’échange de valeur, c’est tout ce qui a de la valeur. Il a une histoire à elle. Nous allons rapidement récapituler l’histoire pour être en mesure de comprendre comment l’argent a évoluer à la façon dont nous le connaissons aujourd’hui, et comment Bitcoin le fait avancer au niveau suivant.

Tout le monde n’a pas tout. Dans le bon vieux temps où il n’y avait aucune notion de monnaie ou d’argent, les gens ont encore compris comment ils pouvaient échanger ce qu’ils avaient en excédent pour ce qu’ils avaient besoin de quelqu’un d’autre. C’était l’époque du système de troc. Le blé en échange de peluches ou d’oranges pour les citrons était le système. Tout cela était bon, mais que se passe-t-il si quelqu’un qui a du blé a besoin de médicaments que l’autre personne n’a pas? Exemple : Alice a du blé et a besoin de médicaments, mais Bob sait qu’elle a accès à quelqu’un qui a des oranges, et Bob a besoin de blé. Dans cette situation, l’échange ne fonctionne pas. Donc, ils doivent trouver une troisième personne, Charlie, qui pourrait avoir besoin d’oranges et a aussi des médicaments excédentaires. Une représentation picturale de ce scénario est présentée à la figure 3-1.

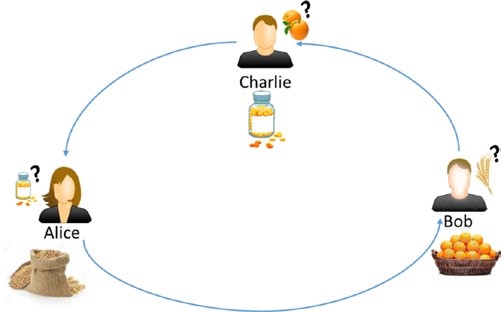
Figure 3-1. Le système primitif de troc

Il a toujours été difficile de trouver une personne comme Charlie dans l’exemple précédent qui pourrait s’adapter dans le puzzle si facilement ; ce problème devait être résolu. Ainsi, les gens ont commencé à penser à un système banalisé d’échange de valeur. Il y avait quelques articles dont tout le monde aurait besoin, comme le lait, le sel, les graines, les moutons, etc. Ce système a presque fonctionné! Peu de temps après, les gens se sont rendu compte qu’il était assez gênant et difficile de stocker de tels produits.

Finalement, de meilleures techniques ont été trouvés pour être utilisés comme instruments financiers, tels que les pièces métalliques. Les gens accordaient plus d’importance aux métaux rares qu’à ceux d’habitude. Les métaux d’or et d’argent sont en tête de liste car ils ne se corroderaient pas. Puis les pays ont commencé à frapper leur propre monnaie (pièces métalliques avec des poids différents) avec leur sceau officiel en eux. Bien que les pièces de métal et les pièces de monnaie étaient meilleures que le système précédent, comme on pouvait facilement les stocker et les transporter, ils étaient vulnérables au vol. Les temples sont venus à la rescousse pour les gens qui avaient confiance en eux et ils avaient une forte conviction que personne ne volerait des temples. Les prêtres donneraient un reçu à la personne déposant de l’or qui mentionnerait la quantité d’or/argent reçu, comme une promesse de reconnaître leur dépôt et de redonner au porteur de la réception la même chose à leur retour. La personne qui porte le reçu pouvait faire circuler le reçu sur le marché pour obtenir ce qu’elle voulait. Ce fut le début de notre système bancaire. Le reçu a fonctionné, comme la monnaie fiduciaire et les temples ont joué le rôle de banques centralisées auxquels les gens faisaient confiance.

Reportez-vous à la figure 3-2 pour comprendre comment ce système est apparu à l’époque.

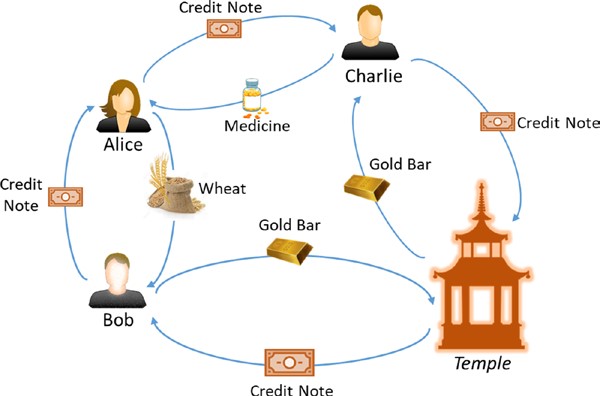
Figure 3-2. Le début de l’ère bancaire

Dans le système qui vient d’être mentionné, la monnaie a toujours été soutenue par certains métaux précieux comme l’or ou l’argent. Ce système s’est poursuivi même après que les gouvernements et les banques ont remplacé les temples. C’est ainsi que la monnaie des produits de base est arrivée sur le marché pour permettre un moyen universel d’échange de valeur pour les biens et services. Quelle que soit la monnaie qui était là à cette époque, elle était tout soutenu par l’or / argent.

Lentement, la « monnaie fiduciaire » a été introduite par les gouvernements comme monnaie légale, qui n’était plus soutenue par l’or ou l’argent. C’était purement fondé sur la confiance, en ce sens que les gens n’avaient pas d’autre choix que de faire confiance au gouvernement. La monnaie Fiat n’a pas de valeur intrinsèque, elle est juste soutenue par le gouvernement.

Ainsi, la valeur de l’argent aujourd’hui dépend de la stabilité et de la performance des gouvernements dans la juridiction de qui la monnaie est émise et utilisée. Ces monnaies papier étaient l’argent et il n’y avait rien de plus précieux dans les banques. C’était l’état des systèmes bancaires et en même temps le monde numérique ne faisait que se former.

Vers les années 1990, le monde de l’Internet prenait de l’ampleur et les systèmes bancaires se numérisaient. Comme un certain niveau d’inconfort était toujours là avec les monnaies fiduciaires, car ils étaient périssables et vulnérables au vol, les banques ont assuré que les gens pouvaient simplement passer au numérique! C’était l’époque où même les billets en papier n’étaient pas tenus d’être imprimés. L’argent est devenu les numéros numériques dans les systèmes informatiques des banques. Aujourd’hui, si chaque titulaire de compte allait à leur banque respective et exigeait les billets de monnaie pour le montant d’argent qu’ils détiennent dans leurs comptes, les banques seraient en grande difficulté! L’argent réel total en circulation est extrêmement marginal par rapport au montant de l’argent numérique dans le monde entier.

Aube de Bitcoin

Dans le premier chapitre, nous avons examiné les aspects technologiques de la révolution Internet, et dans la section précédente de ce chapitre, nous avons examiné l’évolution de l’argent. Nous devrions maintenant les regarder côte à côte pour comprendre le point de vue de Satoshi Nakamoto derrière la conception de Bitcoin, une crypto-monnaie. Dans cette section et ailleurs dans ce texte, nous allons essayer d’éclairer les déclarations de Satoshi dans le document qu’il a écrit sur Bitcoin.

Nous avons appris à connaître les temples, puis les gouvernements et les banques pour le rôle qu’ils ont joué dans les systèmes monétaires qui ont évolué à partir des systèmes de troc. Même aujourd’hui, la situation est la même. Si vous zoomez un peu sur ces systèmes, vous constaterez que la seule chose pivot qui rend ces systèmes stables est l’élément «confiance». Les gens faisaient confiance aux temples, puis ils faisaient confiance aux gouvernements et aux banques. L’ensemble du commerce sur Internet repose aujourd’hui sur des tiers centralisés et dignes de confiance pour traiter les paiements. Bien que l’Internet ait été conçu pour être peer-to-peer, les gens construisent des systèmes centralisés sur elle pour refléter la même vieille pratique. Eh bien, techniquement la construction d’un système peer-to-peer dans les années 2000 a été assez difficile compte tenu de la maturité de la technologie au cours de cette période. Par conséquent, le coût des transactions, le temps pris pour régler une transaction et d’autres questions liées à la centralisation étaient évidents. Ce n’était pas le cas avec les monnaies physiques, car les transactions signifiaient le règlement.

Pourrait-il y avoir une monnaie numérique soutenue par la puissance de calcul, de la même façon que l’or a été utilisé pour soutenir l’argent en circulation ? La réponse est “Oui”, grâce aux Bitcoins de Satoshi. Les Bitcoins sont conçus pour permettre des paiements électroniques entre deux parties sur la base de preuves cryptographiques, et non sur la base de la confiance due à des tiers intermédiaires. C’est possible aujourd’hui grâce des progrès technologiques. Dans ce chapitre, nous verrons comment Satoshi Nakamoto a combiné la cryptographie, la théorie des jeux et les progrès de l’ingénierie informatique pour concevoir le système Bitcoin en 2008. Après sa mise en service en 2009 et jusqu’à aujourd’hui, le système est assez stable et assez robuste pour soutenir tout type de cyberattaques. Elle a résisté à l’épreuve du temps et s’est positionnée comme monnaie mondiale.

Qu’est-ce que Bitcoin ?

Blockchain propose la crypto-monnaie : de l’argent numérique ! Tout comme nous pouvons effectuer des transactions avec des devises physiques sans banques ou autres entités centralisées, Bitcoin est conçu pour faciliter les transactions monétaires peer-to-peer sans intermédiaires de confiance. Examinons ce que c’est, puis apprenons plus tard dans le chapitre comment cela fonctionne vraiment. Bitcoin est une crypto-monnaie décentralisée qui ne se limite à aucune nation et est une monnaie mondiale. Elle est décentralisée sous tous les aspects, techniques, logiques et politiques. Au fur et à mesure que les transactions sont validées, de nouveaux Bitcoins sont extraits et un maximum de 21 millions de Bitcoins peut être produit.

Toute personne ayant une bonne puissance de calcul peut participer à l’exploitation minière et générer de nouveaux Bitcoins. Après que tous les Bitcoins soient générés, aucune nouvelle pièce ne peut être frappée et seules les pièces en circulation seraient utilisées. Notez que les Bitcoins n’ont pas de coupures fixes telles que les monnaies fiduciaires nationales. Selon la conception, les Bitcoins peuvent avoir n’importe quelle valeur avec huit décimales de précision. Ainsi, la plus petite valeur en Bitcoin est 0.00000001 BTC, qui est appelé 1 Satoshi.

Les mineurs extradent les transactions pour frapper de nouvelles pièces et consomment également les frais de transaction que la personne prête à effectuer une transaction est prête à payer. Lorsque le nombre total de pièces atteint 21 millions, les mineurs valideraient les transactions uniquement pour les frais de transaction. Si quelqu’un tente de faire une transaction sans frais de transaction, il peut encore être exploité parce qu’il s’agit d’une transaction valide (si du tout il est) et aussi le mineur est plus intéressé par la récompense de minage qui lui permet de générer de nouvelles pièces.

Vous vous demandez ce qui décide de la valeur des Bitcoins ? Lorsque la monnaie a été soutenue par l’or, elle était facile à évaluer grâce à la valeur basée sur les normes de l’or. Lorsque nous disons que Bitcoin est soutenu par la puissance de calcul que les gens utilisent pour l’exploitation du minage, ce n’est pas suffisant pour comprendre comment il atteint sa valeur. Voici un peu d’économie nécessaire pour le comprendre.

Lorsque la monnaie fiat a été lancée pour la première fois, elle a été soutenue par l’or. Puisque les gens croyaient en l’or, ils croyaient aussi à la monnaie. Après quelques décennies, la monnaie n’était plus soutenue par l’or et dépendait totalement des gouvernements. Les gens ont continué à y croire parce qu’ils forment eux-mêmes ou contribuent à la formation de leur propre gouvernement. Puisque les gouvernements assurent sa valeur, et les gens lui font confiance, de sorte qu’il atteint cette valeur. Dans un contexte international, la valeur de la monnaie de certains pays dépend de divers facteurs et le plus important d’entre eux est « l’offre et la demande ». Il faut garder à l’esprit que certains pays qui ont imprimé beaucoup de billets de monnaie fiat ont fait faillite ; leur économie a baissé ! Il doit y avoir un équilibre et pour comprendre cela, plus d’économie est nécessaire, ce qui est au-delà de la portée de l’article. Revenons donc aux Bitcoins pour l’instant.

Lorsque Bitcoin a été lancé, il n’avait pas de prix officiel. Peu à peu, lorsque l’échange a commencé à avoir lieu, il a développé un prix et un Bitcoin n’était même pas un USD. Étant donné que les Bitcoins sont générés par un processus concurrentiel et décentralisé appelé « mine », et qu’ils sont générés à un taux fixe avec un plafond supérieur de 21 millions de Bitcoins au total qui peut exister, cela fait de Bitcoin une ressource rare. Relatant maintenant ce contexte au jeu de « l’offre et de la demande », la valeur de Bitcoin a commencé à gonfler. Lentement, quand le monde entier a commencé à y croire, son prix a même monté en flèche de quelques USD à des milliers d’USD. L’adoption du Bitcoin parmi les utilisateurs, les commerçants, les start-ups, les grandes entreprises, et bien d’autres se développe comme jamais auparavant parce qu’ils sont utilisés sous forme d’argent. Ainsi, la valeur de Bitcoin est fortement influencée par la « confiance », « l’adoption » et « l’offre et la demande » et son prix est fixé par le marché.

Maintenant, la question est de savoir pourquoi la valeur de Bitcoin est si volatile et fluctue beaucoup. Une raison évidente est l’offre et la demande. Nous avons appris qu’il ne peut y avoir qu’un nombre limité de Bitcoins en circulation, soit 21 millions, et que le rythme auquel ils sont générés diminue avec le temps. En raison de cette conception, il y a toujours un écart dans l’offre et la demande, ce qui entraîne cette volatilité. Une autre raison est que les Bitcoins ne sont jamais échangés en un seul endroit. Il y a tellement d’échanges dans tant d’endroits à travers le monde, et tous ces échanges ont leurs propres prix de change. Les index que vous voyez recueillir les prix de change Bitcoin de plusieurs bourses, puis les moyenne. Encore une fois, puisque tous ces index ne recueillent pas de données à partir du même ensemble d’échanges, même s’ils ne correspondent pas. De même, le facteur de liquidité qui implique le nombre de Bitcoins qui circulent sur l’ensemble du marché à un moment donné influence également la volatilité du prix du Bitcoin. À partir de maintenant, il s’agit certainement d’un actif à haut risque, mais il pourrait se stabiliser avec le temps. Jetons un coup d’oeil à la liste suivante des facteurs qui peuvent influencer l’offre et la demande de Bitcoins, et donc leur prix :

• Confiance des gens dans Bitcoin et peur de l’incertitude
• Couverture médiatique avec de bonnes et de mauvaises nouvelles sur Bitcoin
• Certaines personnes possèdent des Bitcoins et ne leur permettent pas de circuler sur le marché et certaines personnes continuent d’acheter et de vendre pour minimiser les risques. C’est pourquoi le niveau de liquidité de Bitcoin ne cesse de changer.
• Acceptation des Bitcoins par les grands géants du commerce électronique
• Interdiction des Bitcoins dans certains pays

Si vous vous demandez maintenant s’il ya une possibilité de Bitcoin de planter complètement, alors la réponse est “Oui.” Il existe de nombreux exemples de pays dont les systèmes monétaires se sont effondrés. Eh bien, il y avait des raisons politiques et économiques pour eux de s’écraser comme l’hyperinflation, ce qui n’est pas le cas avec les Bitcoins parce que l’on ne peut pas générer autant de Bitcoins qu’ils le veulent et le nombre total de Bitcoins est fixé. Cependant, il existe une possibilité d’échec technique ou cryptographique des Bitcoins. Notons, tout de même que Bitcoin a résisté à l’épreuve du temps depuis sa création en 2008 et il y a une possibilité qu’il aille croître beaucoup plus avec le temps, mais il ne peut pas être garanti !

Travailler avec Bitcoins

Pour commencer avec les Bitcoins, aucune technicité n’est nécessaire. Vous n’avez qu’à télécharger un portefeuille Bitcoin et commencer avec elle. Lorsque vous téléchargez et installez un portefeuille sur votre ordinateur portable ou mobile, il génère votre première adresse Bitcoin (clé publique). Vous pouvez générer beaucoup plus, cependant, et vous devriez. C’est une meilleure pratique d’utiliser les adresses Bitcoin qu’une seule fois. La réutilisation de l’adresse est une pratique involontaire dans Bitcoin, bien qu’elle fonctionne. La réutilisation de l’adresse peut nuire à la vie privée et à la confidentialité. Par exemple, si vous réutilisez la même adresse, en signant une transaction avec la même clé privée, le destinataire peut facilement et de manière fiable déterminer que l’adresse réutilisée est la vôtre. Si la même adresse est utilisée avec plusieurs transactions, ils peuvent tous être suivis et permettre de trouver qui vous êtes devient plus facile.

Rappelez-vous que Bitcoin n’est pas totalement anonyme ; il est dit être pseudonyme et il ya des moyens de retracer les origines de la transaction que peuvent révéler les propriétaires.

Vous devez divulguer votre adresse Bitcoin à la personne désireuse de vous transférer des Bitcoins. C’est très sûr parce que la clé publique est publique de toute façon. Nous savons qu’il n’y a aucune notion d’équilibre de clôture dans Bitcoin et tous les enregistrements sont là comme transactions. Les portefeuilles Bitcoin peuvent facilement calculer leur solde déduisable, car ils ont les clés privées des clés publiques correspondantes sur lesquelles les transactions sont reçues. Il existe une variété de portefeuilles Bitcoin disponibles auprès de tant de fournisseurs de portefeuille. Il y a des portefeuilles mobiles, des portefeuilles de bureau, des portefeuilles Web basés sur le navigateur, des portefeuilles matériels, etc., avec différents niveaux de sécurité. Vous devez être extrêmement prudent dans l’aspect sécurité du portefeuille tout en travaillant avec Bitcoins. Les paiements Bitcoin sont irréversibles.

Vous devez vous demander comment sécuriser ces portefeuilles. Eh bien, différents types de portefeuille ont différentes level de sécurité et cela dépend de la façon dont vous voulez l’utiliser. De nombreux services de portefeuille en ligne ont souffert d’atteintes à la sécurité. C’est toujours une bonne pratique d’activer l’authentification à deux facteurs chaque fois que cela s’applique. Si vous êtes un utilisateur régulier de Bitcoins, il peut être une bonne idée d’utiliser de petites quantités dans vos portefeuilles et de garder le reste séparément dans un environnement sûr. Un portefeuille hors ligne ou un portefeuille froid qui n’est pas connecté au réseau offre le plus haut niveau de sécurité pour les économies. En outre, il devrait y avoir des mécanismes de sauvegarde appropriés pour votre portefeuille au cas où vous perdez votre ordinateur / mobile. Rappelez-vous que si vous perdez votre clé privée, vous perdez tout l’argent qui lui est associé.

Si vous n’avez pas rejoint Bitcoin en tant que mineur exécutant un nœud complet, alors vous pouvez simplement être un utilisateur ou un commerçant de Bitcoins. Vous aurez certainement besoin d’un échange d’où vous pouvez acheter des Bitcoins avec vos euros ou vos dollars américains ou d’autres devises comme accepté par les bourses. Vous devriez préférer acheter des Bitcoins à partir d’un échange légitime et sécurisé. Il y a eu de nombreux exemples d’échanges qui ont souffert d’atteintes à la sécurité.

La Blockchain Bitcoin

Nous avons déjà examiné la structure de données de base de la blockchain dans le chapitre précédent et nous avons également couvert les éléments constitutifs de base d’une structure de données blockchain telles que les techniques de hachage et la cryptographie asymétrique.

Nous allons apprendre les spécificités de la blockchain Bitcoin dans cette section.

La blockchain Bitcoin, comme toute autre blockchain, a une structure de données blockchain similaire. Le client Bitcoin Core utilise la base de données LevelDB de Google pour stocker la structure de données blockchain en interne. Chaque bloc est identifié par son hachage (Bitcoin utilise l’algorithme de hachage SHA256). Chaque bloc contient le hachage du bloc précédent dans sa section d’en-tête. Rappelez-vous que ce hachage n’est pas seulement hachage de l’en-tête précédent, mais l’ensemble du bloc, y compris l’en-tête, et il continue tout le chemin vers le bloc de genèse. Le bloc de genèse est le début de toute blockchain. Typiquement, une blockchain Bitcoin semble comme indiqué dans la figure 3-3.

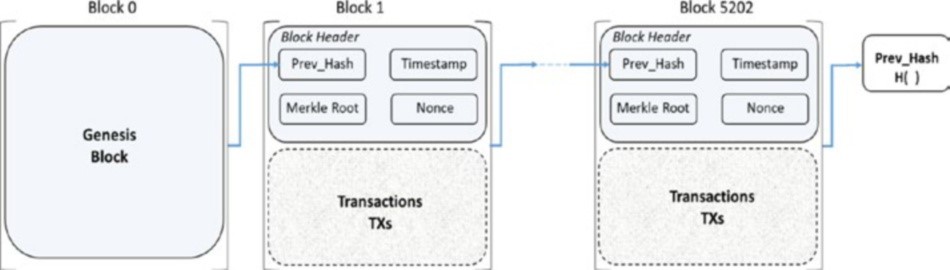
Figure 3-3. La blockchain Bitcoin

Comme vous pouvez le voir dans cette blockchain, il y a une partie en-tête de bloc qui contient les informations d’en-tête et il y a une partie du corps où les transactions sont regroupées dans chaque bloc. L’en-tête de chaque bloc contient le hachage du bloc précédent. Donc, tout changement dans n’importe quel bloc dans la chaîne ne sera pas si facile; tous les blocs suivants doivent être modifiés en conséquence. Exemple : Si quelqu’un tente de modifier une transaction précédente qui a été capturée dans, par exemple, le bloc numéro 441, après avoir modifié la transaction, le hachage de ce bloc qui est dans l’en-tête du bloc numéro 442 ne correspondra pas, il doit donc être changé. Changer l’en-tête avec le nouveau hachage vous demandera alors de mettre à jour le hachage dans l’en-tête de bloc du bloc suivant dans la séquence, qui est le bloc numéro 443, et cela se poursuivra jusqu’au bloc actuel et c’est un travail difficile à faire. Il devient presque impossible quand nous savons que chaque nœud a sa propre copie et le piratage dans tous les nœuds, ou au moins 51% d’entre eux, est impossible.

Dans la blockchain, il n’y a qu’un seul véritable chemin vers le bloc de genèse. Cependant, si vous commencez à partir du bloc de genèse, alors il peut y avoir des fourchettes. Lorsque deux blocs sont proposés en même temps et que les deux sont valides, un seul d’entre eux deviendrait une partie de la vraie chaîne et l’autre devient orphelin. Chaque nœud s’appuie sur la plus longue chaîne, et celui qu’il entend en premier et celui qui devient la plus longue chaîne sera celui sur lequel s’appuyer. Un tel scénario peut être représenté comme indiqué à la figure 3-4.

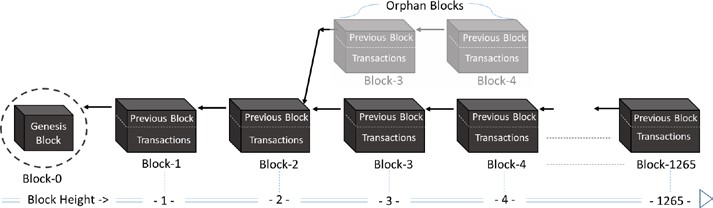
Figure 3-4. Blocs orphelins dans la vraie blockchain

Observez dans la figure 3-4 qu’à hauteur du bloc-3, deux blocs sont proposés pour devenir bloc-3, mais un seul d’entre eux pourrait se rendre à la blockchain finale et le reste est devenu orphelin. Il est évident qu’à une certaine hauteur de bloc, il y a une possibilité d’un ou plusieurs blocs parce qu’il peut aussi bien y avoir quelques blocs orphelins à cette hauteur, ainsi la hauteur de bloc n’est pas la meilleure manière d’identifier un bloc et le hachage de bloc est la bonne manière de faire.

Structure de bloc

La structure de bloc d’une blockchain Bitcoin est fixée pour tous les blocs et dispose de champs spécifiques avec les données correspondantes requises. Jetez un oeil à la figure 3-5, une vue d’oiseau-oeil de la structure entière de bloc, et puis nous apprendrons plus au sujet des champs individuels plus tard dans ce chapitre.

Figure 3-5. Structure de bloc de la blockchain Bitcoin

Une structure de bloc typique apparaît comme indiqué dans le tableau 3-1.

Tableau 3-1. Structure de bloc

Champ	Taille	Description
Numéro magique	4 octets	Il a une valeur fixe 0xD9B4BeF9, qui indique le début du bloc et aussi que le bloc est du réseau principal ou le réseau de production.
Taille du bloc	4 octets	Cela indique la taille du bloc. Les blocs Bitcoin d’origine sont de 1 Mo et il y a une nouvelle version de Bitcoin appelé “Bitcoin Cash” dont la taille du bloc est de 2 Mo.
En-tête de bloc	80 octets	Il comprend beaucoup d’informations telles que les hachages de Blocks, nonce, racine de Merkle, et beaucoup plus.
Compteur de transaction	1 à 9 octets (longueur variable	Il indique le nombre total de transactions qui sont incluses dans le bloc. Toutes les transactions ne sont pas de la même taille, et il y a un nombre variable de transactions dans chaque bloc.
Liste des transactions	Nombre variable mais de taille fixe	Il répertorie toutes les transactions qui se déroulent dans un bloc donné. Selon la taille du bloc (si 1 Mo ou 2 Mo), ce champ occupe l’espace restant dans un bloc.

Zoomons maintenant (tableau 3-2) vers la section “Block Header” des blocs et apprenons les différents champs qu’il maintient.

Tableau 3-2. Composants d’en-tête de bloc

Champ	Taille	Description
Version	4 octets	Il indique le numéro de version du protocole Bitcoin. Idéalement chaque nœud exécutant le protocole Bitcoin devrait avoir le même numéro de version.
Précédent hachage du Bloc	32 octets	Il contient le hachage du bloc en-tête du bloc précédent dans la chaîne. Lorsque tous les champs de l’en-tête de bloc précédent sont combinés et hachés avec l’algorithme sha256, il produit un résultat de 256 bits, qui est de 32 octets.
Racine de Merkle	32 octets	heuses des transactions dans un bloc forment un arbre Merkle par la conception, et la racine de Merkle est le hhasde racine de cet arbre Merkle. si une transaction est modifiée dans le bloc, elle ne correspond pas à la racine Merkle lorsqu’elle est calculée. de cette façon, il garantit que le maintien du hh de l’en-tête du bloc précédent est suffisant pour maintenir la blockchain sécurisée. aussi, les arbres Merkle aider à déterminer si une transaction a été une partie du bloc dans o/n) temps, et sont assez rapides!
Timestamp	4 octets	Il n’y a aucune notion d’une époque mondiale dans le réseau Bitcoin. Ainsi, ce champ indique un temps approximatif de création de bloc dans le format de temps d’Unix.
Difficulté Cible	4 octets	La preuve de travail (pow) niveau de difficulté qui a été fixé pour ce bloc quand il a été extrait
Nonce	4 octets	C’est le nombre aléatoire qui a satisfait le puzzle pow pendant l’exploitation minière.

Les champs de blocs et leurs explications correspondantes telles qu’elles sont présentées dans les tableaux précédents sont assez bonnes pour commencer, et nous allons explorer plus de quelques champs qui nécessitent une explication plus détaillée.

Arbre de Merkle

Nous avons couvert le concept d’arbres Merkle dans le chapitre précédent.

Dans cette section, nous allons simplement jeter un oeil à la façon dont Bitcoin utilise les arbres Merkle. Chaque bloc d’une blockchain Bitcoin contient le hachage de toutes les transactions, et la racine Merkle de toutes ces transactions est incluse dans l’en-tête de ce bloc. D’un sens vrai, lorsque nous disons que chaque en-tête de bloc contient le hh de l’ensemble du bloc précédent, la confiance est qu’il contient juste le hachage de l’en-tête du bloc précédent. Néanmoins, il suffit, parce que l’en-tête contient déjà la racine de Merkle. Si une transaction dans le bloc est modifiée, la racine merkle ne correspondra plus et une telle conception conserve encore l’intégrité de la blockchain.

L’arbre Merkle est une structure de données d’arbre du hachage des transactions. Les « nœuds de feuilles » dans l’arbre de Merkle représentent réellement le hhas des transactions, alors que la racine de l’arbre est la racine de Merkle. Reportez-vous à la figure 3-6.

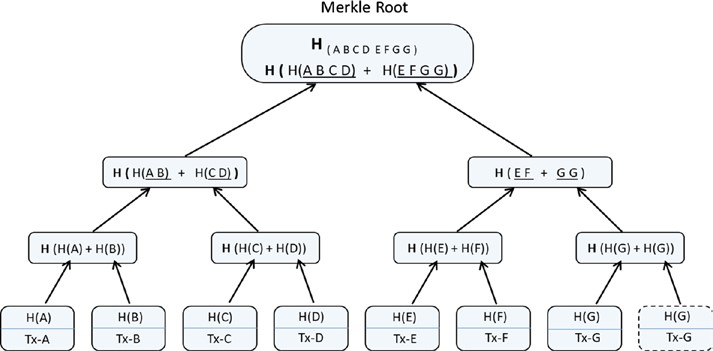
Figure 3-6. Représentation de Merkle-arbre

Notons que le hachage des sept transactions A, B, C, D, E, F et G forment la feuille de l’arbre. Puisqu’il y a sept transactions mais les nœuds de feuille totaux devraient être même dans un arbre binaire, le dernier nœud de feuille obtient répété. Chaque hachage de transaction de 32 octets (c.-à-d. 256 bits) est calculé en appliquant SHA256 deux fois aux transactions. De même, le hon de deux transactions est concatenated (62 octets) et ensuite hâté deux fois avec SHA256 pour obtenir le hon parent de 32 octets.

Seule la voie Merkle vers une transaction est suffisante pour vérifier si une transaction faisait partie d’un bloc et est donc assez efficace. Ainsi, la blockchain réelle peut être représentée comme indiqué dans la figure 3-7.

Figure 3-7. Représentation d’arbre de Merkle

Cible de difficulté

La cible de difficulté est celle qui conduit le PoW en Bitcoin. L’idée est qu’une fois qu’un bloc est rempli de transactions valides, le hachage de l’en-tête de ce bloc doit être calculé pour être inférieur à la cible de difficulté dans le même en-tête. Le nonce dans l’en-tête commence à partir de zéro. Le mineur doit continuer à incrémenter ce nonce et haché l’en-tête jusqu’à ce que la valeur de hachage soit inférieure à la cible.

Les bits de difficulté de quatre octets (32 bits) dans les en-têtes définissent quelle serait la valeur cible (256 bits) pour que ce bloc soit extrait. Le nonce doit être trouvé de telle sorte que le hachage de l’en-tête entier devrait être inférieur à la valeur cible. Rappelez-vous que plus la valeur cible est faible, plus il serait difficile de trouver un hachage d’en-tête qui serait inférieur à la cible. Depuis Bitcoin utilise SHA256, chaque fois que vous hachez un bloc d’en-tête, la sortie est n’importe quel nombre entre 0 et 2²⁵⁶, qui est tout à fait un grand nombre.

Si avec votre nonce le hachage est inférieur à la cible, le bloc sera accepté par l’ensemble du réseau, sinon vous devez essayer avec un nonce différent jusqu’à ce qu’il satisfasse la condition. À ce stade, il n’est toujours pas clair comment la cible de difficulté est calculée avec les bits de difficulté dans chaque en-tête.

La cible peut être dérivée des bits de difficulté à quatre octets (8 nombres hexadécimals) dans l’en-tête en utilisant une formule prédéfinie que chaque nœud a par défaut, car il est venu avec les binaires pendant l’installation. Voici la formule pour calculer la difficulté :

Cible = coefficient * 2^{(8*(exposant-3))}

Notez qu’il y a un « coefficient » et qu’il y a aussi un terme « exposant » dans cette formule, qui sont présents dans le cadre des bits de difficulté à quatre octets. Prenons un exemple pour mieux l’expliquer. Si les bits de difficulté à quatre octets sous forme de hexagone sont 0x1b0404cb, alors les deux premiers chiffres hexagonaux forment le terme exposant, qui est (0x1b), et le reste forme le terme de coefficient, qui est (0x0404cb) dans ce cas. Résoudre pour la formule cible avec ces valeurs :

Cible = 0x0404cb * 2^{(0x08 * (0x1b – 0x03))}

CB000000000000000000000000000000000000000000000000

Bitcoin est conçu de telle sorte que tous les 2 016 blocs devraient prendre deux semaines pour être générés et si vous faites le calcul, il serait d’environ dix minutes pour chaque bloc. Dans ce réseau asynchrone, il est difficile de programmer comme ça où chaque bloc prend exactement dix minutes avec le genre de mécanisme PoW en place. En réalité, c’est le temps moyen pour un bloc, et il y a une possibilité qu’un bloc Bitcoin est généré dans une minute ou il peut très bien prendre 15 minutes pour être généré. Ainsi, la difficulté est conçue pour augmenter ou diminuer selon qu’il a fallu moins ou plus de deux semaines pour trouver 2 016 blocs. Ce temps pris pour 2 016 blocs peut être trouvé en utilisant le temps présent dans les champs d’horodatage de chaque en-tête de bloc. S’il a fallu, disons, t quantité de temps pour 2.016 blocs, ce qui n’est jamais exactement deux semaines, la cible de difficulté dans chaque bloc est multiplié par (T / 2 semaines). Ainsi, le résultat de [cible de difficulté – (T / 2semaines)] sera augmenté si T était moins et diminué autrement.

Il est maintenant évident que la cible de difficulté est réglable; elle pourrait être fixé plus difficile ou plus facile en fonction de la situation que nous avons expliqué avant. Vous devez vous demander, qui ajuste cette difficulté lorsque le système est décentralisé ? Une règle de base que vous devez toujours garder à l’esprit est que tout ce qui se passe dans une conception aussi décentralisée doit se produire individuellement à chaque nœud. Après chaque 2 016 blocs, tous les nœuds calculent individuellement la nouvelle valeur cible de difficulté et ils concluent tous sur le même parce qu’il existe déjà une formule définie pour cela. Pour avoir cette formule à portée de main, le voici une fois de plus:

Nouvelle cible = ancienne cible * (T / 2 semaines)

Nouvelle cible = ancienne cible (Temps pris pour 2016 Blocs en secondes / 12,09,600 secondes)

Les paramètres tels que 2 016 blocs et TargetTimespan de deux semaines (12 09 600 secondes) sont définis dans chainparams.cpp comme indiqué ci-après :

consensus.nPowTargetTimespan = 14 * 24 * 60 * 60; // deux semaines consensus.nPowTargetSpacing = 10 à 60; consensus.nMinerConfirmationWindow = 2016;
nPowTargetTimespan / nPowTargetSpacing

Notez ici qu’il est (T / 2 semaines) et non (2 semaines / T). L’idée est de diminuer la cible de difficulté quand il est nécessaire d’augmenter la complexité, de sorte qu’il faut plus de temps. Plus le hachage cible est bas, plus il est difficile de trouver un hachage qui est inférieur à ce hachage cible. Exemple : S’il a fallu dix jours pour extraire 2 016 blocs, alors (T / 2 semaines) serait une fraction, qui, lorsqu’elle est multipliée par « Vieille cible », la réduit davantage et que la « nouvelle cible » serait une valeur inférieure à l’ancienne. Cela rendrait difficile de trouver un hachage et nécessiterait plus de temps. C’est ainsi que le temps entre les blocs est maintenu à dix minutes en moyenne. Imaginez que l’objectif de difficulté était fixe et non réglable ; Quel serait, selon vous, le problème ? Rappelez-vous que la puissance de calcul du matériel augmente avec le temps grâce aux ordinateurs plus puissants qui sont introduits et qui améliore l’efficacité de l’extraction de blocs. Une situation où des blocs de 10 ou 100 ou même de 1 000 blocs sont proposés en même temps n’est pas souhaitable pour que le réseau fonctionne correctement. Ainsi, l’idée est que, même lorsque les nœuds informatiques de plus en plus puissants entrent dans le réseau Bitcoin, le temps moyen requis pour proposer un bloc devrait encore être de dix minutes en ajustant la cible de difficulté. En outre, les chances d’un mineur de proposer un bloc dépend de la puissance de hachage qu’ils ont comparée à la puissance mondiale de hachage de tous les mineurs inclus.

Tu te demande s’il y a dix minutes, et pourquoi pas 12 minutes ? Ou pourquoi pas six minutes ? Il suffit de garder à l’esprit qu’il doit y avoir un certain écart de temps pour tous les nœuds dans un système asynchrone décentralisé pour s’entendre sur elle. S’il n’y avait pas d’écart de temps, tant de blocs arriveraient avec juste des retards fractionnels et il n’y aurait pas d’avantage d’optimisation de la blockchain par rapport à la chaîne de transaction. Chaque transaction est une diffusion et chaque nouveau bloc est aussi une diffusion. En outre, la commande qu’une blockchain apporte au système est tout à fait infaisable par la chaîne de transaction. Avec le concept de blocs, il est possible d’inclure les transactions non liées de n’importe quel expéditeur à n’importe quel récepteur dans les blocs, ce qui n’est pas facile à maintenir avec la chaîne de transaction. Une diffusion en bloc valide est plus efficace par rapport à la diffusion de transactions individuelles après validation. Maintenant, pour en revenir à la discussion de dix minutes, il peut très bien être un peu moins ou un peu plus, mais il devrait certainement y avoir un certain écart entre deux blocs consécutifs. Imaginez que vous êtes un mineur et le numéro de bloc miné 4567, mais un autre mineur a eu de la chance et a proposé le numéro de bloc 4567, que vous venez de recevoir tout en résolvant le puzzle cryptographique. Ce que vous feriez maintenant est de valider ce bloc et si elle est valide, l’ajouter à votre copie locale de la blockchain et immédiatement commencer le minage du bloc 4568. Vous ne voudriez pas que quelqu’un d’autre propose déjà le bloc 4568 alors que vous venez de terminer la validation du bloc 4567, que vous avez reçu un peu plus tard par rapport à d’autres mineurs en raison de la latence du réseau. Maintenant, la question est: est-ce 10 minutes la meilleure option possible? Eh bien, il est difficile d’expliquer cela en un mot, mais un écart de dix minutes répond à beaucoup de problèmes en raison d’un réseau asynchrone, retards de temps, perte de paquets, capacité du système, et plus encore. Il est possible qu’il pourrait être optimisé plus loin, disons, cinq minutes ou plus, que vous pouvez voir dans de nombreuses nouvelles crypto-monnaies et d’autres cas d’utilisation blockchain.

Le bloc de genèse

Le tout premier bloc comme vous pouvez le voir dans le code suivant, le bloc-0, est appelé le bloc de genèse. Rappelez-vous que le bloc de genèse doit être codé en dur dans les applications blockchain et c’est le cas avec Bitcoin. Vous pouvez le considérer comme un bloc spécial car il ne contient aucune référence aux blocs précédents. Le bloc de genèse du Bitcoin a été créé en 2009 lors de son lancement. Si vous ouvrez le noyau Bitcoin, en particulier le fichier chainparams. cpp, vous verrez comment le bloc de genèse est encodé statiquement. En utilisant une référence de ligne de commande à Bitcoin Core, vous pouvez obtenir les mêmes informations en interrogeant avec le hhissement du bloc de genèse comme indiqué ci-dessous:

$ bitcoin-cli getblock 000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f

Sortie de la commande précédente :

{

“hash” : “000000000019d6689c085ae165831e934ff763ae46a2a6 c172b3f1b60a8ce26f”,

“confirmations” : 308321,

“taille” : 285,

“hauteur” : 0,

“version” : 1,

“merkleroot” : “4a5e1e4baab89f3a32518a88c31bc87f618 f76673e2cc77ab2127b7afdeda33b”,

“tx” : [“4a5e1e4baab89f3a32518a88c31bc87f618f7673e2cc 77ab2127b7afdeda33b”],

“temps” : 1231006505,

“nonce” : 2083236893,

“bits” : “1d00ffff”,

“difficulté” : 1,00000000,

“nextblockhash” : “00000000839a8e6886ab5951d76 f411475428afc90947e320161bbf18eb6048”

}

Si vous convertissez l’horodatage Unix tel qu’indiqué dans la sortie précédente, vous trouverez cette date-heure d’information : Samedi 3 Janvier 2009 11:45:05 PM. Vous pouvez aussi bien obtenir les mêmes informations sur le site https://blockchain.info. Il suffit de naviguer vers ce site et coller la valeur de hh dans la boîte de recherche supérieure droite et appuyez sur “Enter” Voici ce que vous trouverez (tableau 3-3)

Tableau 3-3. Informations sur les transactions

Résumé
Nombre de transactions	1
Total de la production	50 BtC
Volume estimatif des transactions	0 BtC
Frais de transaction	0 BtC
Hauteur	0 (Chaîne principale)
Timestamp	2009-01-03 18:15:05
Temps reçu	2009-01-03 18:15:05
Relayé par	Inconnu
Difficulté	1
Bits	486604799
Taille	0,285 kB
Poids	0,896 kwU
Version	1
Nonce	2083236893
Récompense de bloc	50 BtC

Tableau 3-4. Informations de hachage

Hachages
Hachage	0000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f
Bloc précédent	0000000000000000000000000000000000000000000000000000000000000000
Bloc suivant (s)	0000000839a8e6886ab5951d76f411475428afc90947e320161bbf18eb6048
Racine de Merkle	4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b

Dans ce Bloc-0, il n’y a qu’une seule transaction, qui est une transaction de base de pièces. Les transactions de base de pièces sont les transactions que les mineurs obtiennent. Il n’y a pas d’entrées à de telles transactions et ils ne peuvent générer de nouveaux Bitcoins. Si vous avez exploré les transactions associées dans ce bloc, voici à quoi il ressemblerait (figure 3-8).

Figure 3-8. Transaction Coinbase dans le bloc-0

Le bitcoin Network

Le réseau Bitcoin est un réseau peer-to-peer, comme nous l’avons déjà vu. Il n’y a pas de serveur centralisé dans un tel système et chaque nœud est traité de manière égale. Il n’y a pas de phénomènes d’esclaves et pas de hiérarchie dans un tel système. Étant donné que cela s’exécute sur Internet lui-même, il utilise la même pile de protocole TCP/IP comme indiqué dans la figure 3-9.

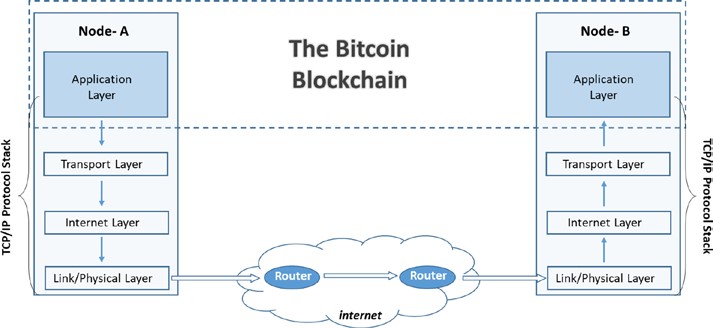
Figure 3-9. Le réseau blockchain Bitcoin sur Internet

Le diagramme ci-dessus montre comment les réseaux Bitcoin coexistent sur la même pile Internet. Le réseau Bitcoin est assez dynamique dans le sens où les nœuds peuvent rejoindre et quitter le réseau à volonté et le système fonctionne toujours. En outre, en dépit d’être de nature asynchrone et avec des retards de réseau et des pertes de paquets, le système est très robuste, grâce à la conception de Bitcoin !

Le réseau Bitcoin est un réseau décentralisé sans point central de défaillance et sans autorité centrale. Avec une telle conception, comment évalueriez-vous la taille du réseau Bitcoin? Il n’y a aucun moyen approprié d’estimer cela car les nœuds peuvent se créer et disparaitre à volonté. Cependant, il y a quelques tentatives de recherche sur le réseau Bitcoin, et certains prétendent qu’il ya près de 10.000 nœuds qui sont pour la plupart connectés au réseau tout le temps et il peut y avoir des millions de nœuds à la fois.

Chaque nœud du réseau Bitcoin est égal en termes d’autorité et a une structure plate, mais les nœuds peuvent être des nœuds complets ou des nœuds légers. Les nœuds complets peuvent effectuer presque toutes les activités autorisées dans le système Bitcoin, telles que les transactions minières et les transactions de radiodiffusion, et peuvent fournir des services de portefeuille. Les nœuds complets fournissent également la fonction de routage pour participer à maintenir le réseau Bitcoin. Pour devenir un nœud complet, vous devez télécharger l’ensemble de la base de données blockchain qui contient l’ensemble des transactions effectuées jusqu’à présent. En outre, le nœud doit rester connecté en permanence au réseau Bitcoin et entendre toutes les transactions en cours. Il est important que vous ayez une bonne connexion réseau, un bon stockage (au moins 200 Go), et au moins 2 Go de RAM qui lui soit dédié. Cette exigence peut encore changer et exiger plus de ressources avec le temps.

D’autre part, les nœuds légers ne peuvent pas extraire de nouveaux blocs mais peuvent vérifier les transactions en utilisant la vérification simplifiée des paiements (SPV). Ils sont autrement appelés « clients légers ». Une grande majorité des nœuds du réseau Bitcoin sont des SPV. Ils peuvent aussi bien participer au minage de pool où il y a beaucoup de nœuds essayant d’extraire de nouveaux blocs ensemble. Les nœuds légers peuvent aider à vérifier les transactions pour les nœuds complets. Un bon exemple d’un SPV est un portefeuille (le client). Si vous exécutez un portefeuille et que quelqu’un vous envoie de l’argent, vous pouvez agir comme un nœud dans le réseau Bitcoin et télécharger les transactions pertinentes à celle qui vous est faite afin que vous puissiez vérifier si la personne qui vous envoie des Bitcoins les possédait réellement.

Il est important de noter qu’un SPV n’est pas aussi sécurisé qu’un nœud entièrement valide, car il contient généralement les en-têtes de bloc et non les blocs entiers. En conséquence, les SPV ne peuvent pas valider les transactions puisqu’ils ne les ont pas pour un bloc et aussi parce qu’ils n’ont pas toutes les sorties de transactions non dépensées (UTXOs) à l’exception de leurs propres transactions.

Découverte de réseau pour un nouveau nœud

Maintenant, pensez, quand un nouveau nœud veut rejoindre le réseau, comment serait-il contacter le réseau? Ce n’est pas un intranet avec un réseau 192.168.1.X où vous pouvez diffuser à l’IP 192.168.1.255 de sorte que n’importe quel ordinateur est une partie du réseau 192.168.1.X reçoit le message de diffusion.

Les commutateurs réseau sont conçus pour permettre de tels paquets de diffusion. Cependant, rappelez-vous que nous parlons d’Internet, sur lequel Bitcoin fonctionne. Si vous exécutez un nœud à Londres, il y a une possibilité qu’il y ait d’autres nœuds à Londres, en Russie, en Irlande, aux États-Unis et en Inde et tous sont connectés via Internet avec une adresse IP face au public.

La question ici est que quand un nouveau nœud rejoint le réseau, comment peut-il comprendre les nœuds pairs? Il n’y a pas de serveur central quelque part pour répondre à leur demande de la façon dont fonctionne une application Web Internet typique. La Blockchain est décentralisée. Lorsqu’il est lancé pour la première fois, un programme Bitcoin Core ou BitcoinJ, il n’a pas l’adresse IP d’un nœud complet. Ainsi, ils sont équipés de plusieurs méthodes pour trouver les pairs. L’une d’entre elles est celle des « seeds » DNS. Plusieurs « seeds » DNS y sont codées en dur. En outre, plusieurs noms d’hôtes sont maintenus dans le système DNS qui résolvent une liste d’adresses IP qui exécutent les nœuds Bitcoin. Les « seeds » DNS sont maintenues par les membres de la communauté Bitcoin. Certains membres de la communauté fournissent des « seeds » DNS statiques en entrant manuellement les adresses IP et les numéros de port. En outre, certains membres de la communauté fournissent des serveurs de démarrage DNS dynamiques qui peuvent automatiquement obtenir les adresses IP des nœuds Bitcoin actifs qui s’exécutent sur les ports Bitcoin par défaut (8333 pour mainnet et 18333 pour testnet). Si vous effectuez des NSLOOKUPs sur les « seeds » DNS, vous obtiendrez un tas d’adresses IP exécutant des nœuds Bitcoin.

Les clients (Bitcoin Core ou BitcoinJ) maintiennent également une liste codée en code dur d’adresses IP qui pointent vers certains nœuds Bitcoin stables (pas un!). Ces nœuds peuvent être appelés nœuds bootstrap dont les points de terminaison sont déjà disponibles avec le code source lui-même. Chaque fois que l’on télécharge les binaires, une nouvelle liste de nœuds actifs sont téléchargés avec les binaires. Une fois qu’une connexion de nœud Bitcoin est établie, il est très facile de tirer la liste des autres nœuds Bitcoin actifs à ce moment-là. Une représentation picturale de la façon dont un nouveau nœud devient une partie du réseau peut être trouvée dans les chiffres suivants. Étape 1 :

Imaginez qu’il y avait six nœuds actifs à un moment donné dans le réseau Bitcoin. Reportez-vous à la figure 3-10.

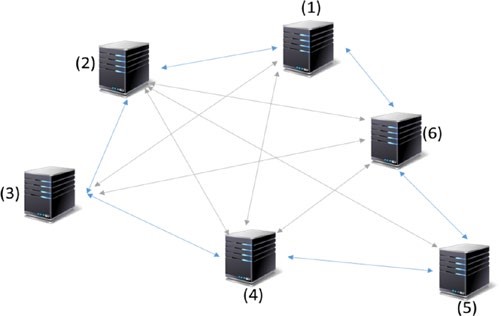
Figure 3-10. Le réseau Bitcoin en général

Étape 2 :

Il y a un nouveau nœud, par exemple, un septième nœud qui vient d’être montré et tente de rejoindre le réseau Bitcoin existant, mais n’a pas encore de connexion. Reportez-vous à la figure 3-11.

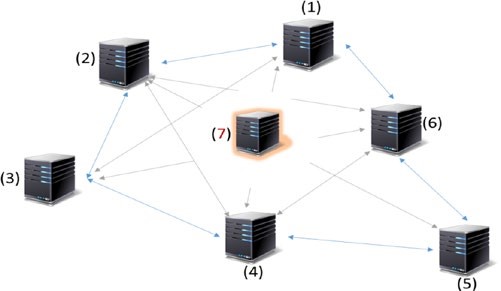
Figure 3-11. Un nouveau nœud essayant de rejoindre le réseau

Étape 3 :

Le septième nœud tentera d’atteindre autant de nœuds qu’il peut soit en utilisant des « seeds » DNS ou en utilisant la liste des nœuds Bitcoin stables dans la liste qu’il a, comme indiqué dans la figure 3-12.

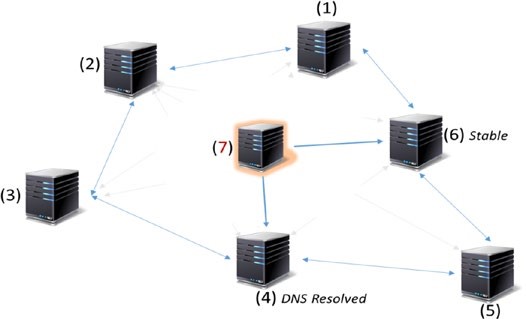
Figure 3-12. Un nouveau nœud Bitcoin contacte certains pairs

Dans le diagramme, nous avons ignoré la partie résolution DNS. C’est la même chose que lorsque vous naviguez sur n’importe quel site Web avec son nom et après la résolution DNS l’adresse IP est récupérée, qui est ensuite utilisé comme adresse du serveur Web de destination pour envoyer des paquets TCP. Pour se connecter à un nouveau pair, le nœud établit une connexion TCP sur le port 8333 (port 8333 est bien connu pour les Bitcoins, mais pourrait être différent). Ensuite, les deux nœuds partagent des informations telles que le numéro de version, le temps, les adresses IP, la hauteur de la blockchain, etc. Le code Bitcoin réel pour le message “Version” défini dans net.cpp est comme indiqué dans les éléments suivants:

PushMessage( “version”, PROTOCOL_VERSION, nLocalServices, nTime, addrYou, addrMe, nLocalHostNonce, FormatSubVersion(CLIENT_NAME, CLIENT_VERSION, std::vector<string>()), nBestHeight, true );

Grâce à ce message Version, la compatibilité entre les deux nœuds est vérifiée comme première étape vers une communication ultérieure.

Étape 4 :

Dans la quatrième étape, les nœuds demandés répondront avec la liste des adresses IP et les numéros de port correspondants des autres nœuds Bitcoin actifs dont ils sont au courant. Veuillez noter qu’il est possible pour certains nœuds actifs de ne pas être au courant de chaque nœud Bitcoin dans le réseau à tout moment. Le numéro de port est important parce qu’une fois que les paquets TCP atteignent le nœud de destination, c’est le numéro de port qui est utilisé par le système d’exploitation pour diriger le message vers l’application/processus correct fonctionnant sur le système. Veuillez consulter la figure 3-13.

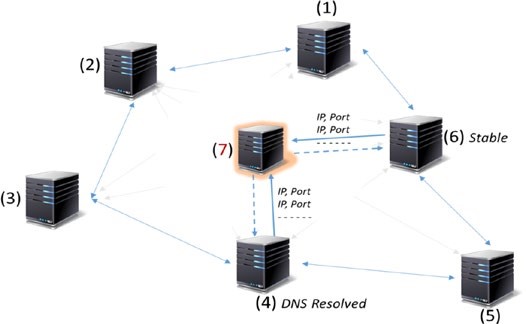
Figure 3-13. Les nœuds Bitcoin peer répondent à la demande du réseau par un nouveau nœud

Notez qu’un seul pair peut suffire à la connexion d’un nœud au réseau Bitcoin ; le nœud doit continuer à découvrir et à se connecter à de nouveaux pairs. C’est parce que les nœuds vont et viennent à volonté et aucune connexion n’est fiable.

Étape 5 :

Dans la cinquième étape, le nouveau septième nœud établit la connexion avec tous les nœuds Bitcoin accessibles, en fonction de la liste qu’il a reçu des nœuds contactés dans l’étape précédente. La figure 3-14 en représente la situation.

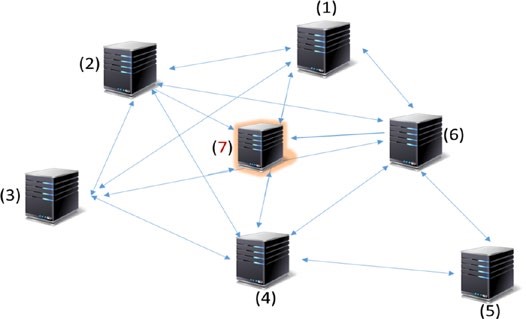
Figure 3-14. Un nouveau nœud fait partie du réseau Bitcoin

Bitcoin Transactions

Les transactions Bitcoin sont les éléments fondamentaux du système Bitcoin. Il existe essentiellement deux catégories plus larges de transactions Bitcoin :

• Transaction Coinbase : Chaque bloc de la blockchain Bitcoin contient une transaction de base de pièces incluse par les mineurs eux-mêmes pour pouvoir extraire de nouvelles pièces. Ils n’ont pas le contrôle du nombre de pièces qu’ils peuvent extraire dans chaque bloc parce qu’il est contrôlé par le réseau lui-même. Il a commencé avec 50 BTC au début et continue de réduire de moitié jusqu’à ce qu’il atteigne 21 millions de Bitcoins au total.
• Transactions régulières : Les transactions régulières sont très similaires aux échanges de devises en général, où l’on essaie de traiter une certaine quantité d’argent qu’ils possèdent avec un autre. Typiquement, dans Bitcoin, tout est présent comme transactions. Pour dépenser un peu de montant, il faut consommer des transactions précédentes où ils ont reçu ce montant, ce sont des transactions régulières en Bitcoin. Dans ce chapitre, nous nous concentrerons principalement sur ces transactions régulières.

Chaque propriétaire d’un Bitcoin peut transférer la pièce à quelqu’un d’autre en signant numériquement un hachage de la transaction précédente où il avait reçu le Bitcoin avec la clé publique du destinataire. Le bénéficiaire ou le destinataire a déjà la clé publique du payeur afin qu’il puisse vérifier la transaction. La figure suivante (figure 3-15) est tirée du livre blanc de Satoshi Nakamoto qui démontre de façon picturale comment il fonctionne.

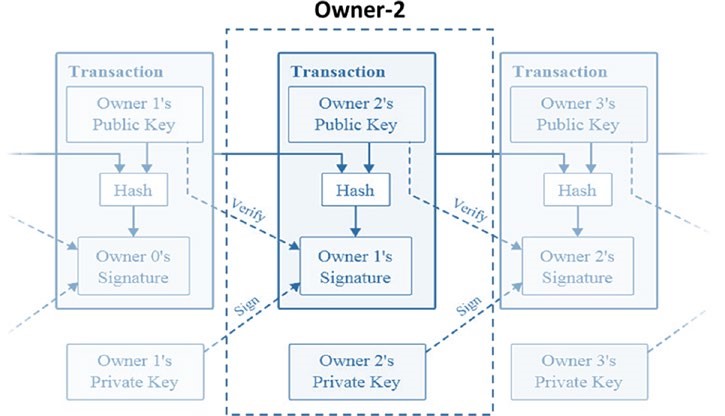
Figure 3-15. Transaction Bitcoin

Notez uniquement la section owner-2 en surbrillance dans le diagramme. Étant donné que owner-1 est à l’origine de cette transaction, il utilise sa clé privée pour signer le hachage de deux éléments : l’un est la transaction précédente où il a lui-même reçu le montant et le second est la clé publique du owner-2. Cette signature peut être facilement vérifiée à l’aide de la clé publique de owner-1 pour s’assurer qu’il s’agit d’une transaction légitime. De même, lorsque le owner-2 initialisera un transfert au owner-3, il utilisera sa clé privée pour signer le hachage de la transaction précédente (celle qu’il a reçue du owner-1) ainsi que la clé publique du owner-3. Une telle transaction peut être, et sera, vérifiée par toute personne qui fait partie du réseau. Évidemment, parce que chaque transaction est diffusée, la plupart des nœuds auront toute l’historique des transactions pour être en mesure d’empêcher les tentatives de double dépense.

Il n’y a pas de principe de clôture du solde dans un réseau Bitcoin, et le montant total que l’on détient est la somme de toutes les transactions entrantes aux adresses publiques que vous possédez. Vous pouvez créer autant d’adresses publiques que vous le souhaitez. Si vous avez dix adresses publiques, quelles que soient les transactions effectuées à cette adresse publique, vous pouvez passer ces transactions (transactions non dépensées ou UTXOs) en utilisant votre clé privée. Si vous devez dépenser, disons, cinq Bitcoins, vous avez un couple de choix :

• Utilisez l’une des transactions précédentes où vous avez reçu cinq Bitcoins ou plus. Transférez cinq Bitcoins au destinataire, certains montants en tant que frais de transaction et le reste à vous-même. Reportez-vous à la figure 3-16.

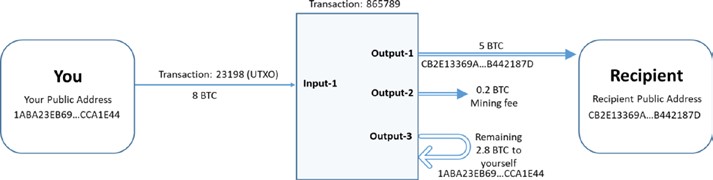
Figure 3-16. Transaction Bitcoin avec une entrée de transaction

• Utilisez plusieurs transactions précédentes que vous aviez reçues qui résumerait à plus de cinq Bitcoins. Transférez cinq Bitcoins au réceptif, certains montants en tant que frais de transaction et le reste à vous-même. Reportez-vous à la figure 3-17.

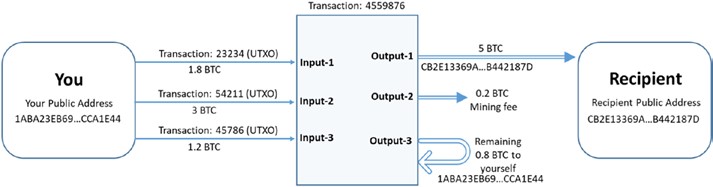
Figure 3-17. Transaction Bitcoin avec entrée de transactions multiples

Comme vous pouvez le voir, chaque transaction prend comme entrée la transaction précédente. Il n’y a aucun compte maintenu qui dit que vous avez huit BTC, et vous pouvez dépenser n’importe quoi au-dessous de ce montant ; si vous dépensez cinq BTC, le solde restant serait de trois BTC. Dans Bitcoin, tout est une transaction où il y a des entrées et des sorties. Si les sorties ne sont pas encore dépensées, ce sont les UTXOs.

Nous sommes conscients que chaque transaction du réseau est diffusée sur l’ensemble du réseau. Que quelqu’un maintienne un nœud ou non, il peut toujours effectuer une transaction et cette transaction est publiée sur tous les nœuds Bitcoin accessibles. Les nœuds Bitcoin récepteurs diffusent ensuite les transactions vers d’autres nœuds et l’ensemble du réseau est généralement inondé de transactions. C’est ce qu’on appelle parfois le protocole de commérages (« gossip ») et joue un rôle important dans la prévention des attaques à double dépense. Se rappeler, à partir du chapitre 2, que la seule façon d’éviter les doubles dépenses est d’être au courant de toutes les transactions.

Chaque nœud maintient un ensemble de toutes les transactions dont il entend parler et ne diffuse que les nouvelles, qui ne faisaient pas déjà partie de la liste. Les nœuds maintiennent les transactions dans la liste jusqu’au moment où la transaction entre dans un bloc et fait partie de la blockchain. C’est parce qu’il y a une chance que même si un bloc a toutes les transactions valides et est proposé comme un bloc valide, il peut encore devenir orphelin en ne faisant pas partie de la plus longue chaîne. Une fois qu’il est confirmé que le bloc fait maintenant partie de la chaîne la plus longue, les transactions qui sont là dans ce bloc sont retirés de la liste des transactions. Chaque nœud complet dans le réseau Bitcoin doit maintenir la liste complète des transactions non dépensées (UTXOs) même si elles sont dans les millions. Si une transaction est dans la liste des UTXOs, alors il peut ne pas être une tentative de double dépense. Lors de la confirmation d’une transaction n’étant pas une attaque de double dépense et aussi la validation des transactions à partir d’autres perspectives, un nœud diffuse de telles transactions. Si vous vous demandez à quelle vitesse la recherche au sein des millions d’UTXOs se fait pour vérifier les doubles dépenses, vous êtes sur la bonne voie. Étant donné que les sorties de transaction sont commandées par leurs hachages, la recherche d’un élément dans une liste de hachage ordonnée est assez rapide.

Réfléchissons maintenant et approfondissons un scénario de double dépense. Il est très possible qu’Alice (A) essaie de payer à Bob (B) et Charlie (C) la même transaction (l’entrée à une transaction est une transaction précédente et il n’y a pas de concept de solde de clôture). Un tel scénario apparaîtrait comme indiqué à la figure 3-18.

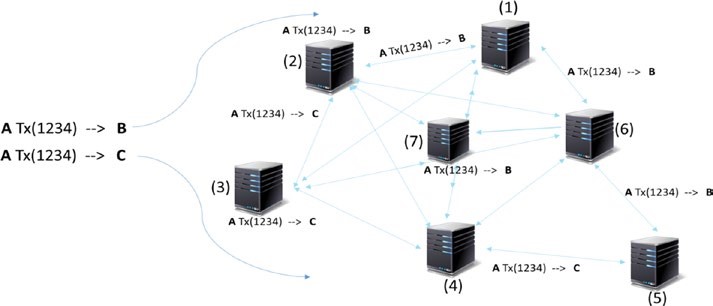
Figure 3-18. Un scénario de transaction à double dépense dans le réseau Bitcoin

Notez dans le chiffre les scénarios suivants :

• A essaie de passer la même transaction à B et C.
• Node-2 a reçu la transaction A Tx(1234) B et
• Node-3 a reçu la transaction A Tx(1234) C.
• Pour le Node-2 et le Node-3, leurs transactions respectives reçues étaient des transactions légitimes.
• Lorsque Node-3 tente de diffuser la transaction A Tx(1234) C to Node-2 (chaque nœud diffuse de nouvelles transactions), Node-2 refuserait cette transaction parce qu’il a déjà une transaction « A Tx(1234) B » avec la même transaction d’entrée Tx(1234).
• Des choses similaires se produisent avec d’autres nœuds, et ils peuvent avoir soit la transaction « A Tx(1234) B » ou « A Tx(1234) C“, selon celui qui les a atteints plus rapidement, mais pas les deux.
• Pendant le minage, quel que soit le nœud qui peut proposer le bloc, il comprendra la transaction qu’il a. Cette transaction ferait partie de la blockchain et le reste des nœuds qui détiennent l’autre transaction l’abandonneraient parce qu’il ne serait plus un UTXO.

Consensus et minage de blocs

Dans la section précédente, nous avons examiné les transactions granulaires. Nous allons apprendre comment les transactions sont regroupées pour former un bloc et un consensus est atteint entre les nœuds, de sorte que l’ensemble du réseau accepte ce bloc pour étendre la blockchain. Notez que le « minage de blocs » se réfère à la création réussie d’un nouveau bloc dans la blockchain. Dans Bitcoin, c’est l’algorithme de consensus PoW distribué qui aide à extraire de nouveaux blocs en maintenant la décentralisation. Il est très difficile de parvenir à un consensus distribué dans un tel réseau. Bien qu’il ait été autour depuis des décennies pour les systèmes distribués tels que Facebook, Google, Amazon, et beaucoup plus parce qu’ils ont des millions de serveurs qui nécessitent une cohérence dans les données qu’ils stockent, le terme consensus est très popularisé en raison de Bitcoins. Dans ce chapitre, nous allons entrer dans les rouages du consensus et du minage.

Tout d’abord, il suffit de garder à l’esprit que tout dans un réseau Bitcoin est représenté comme des transactions. Si vous souhaitez effectuer une transaction, vous devez consommer une ou plusieurs transactions précédentes comme entrée et effectuer une autre transaction. Nous savons déjà qu’il faut signer une transaction en utilisant sa clé privée pour s’assurer que la bonne personne effectue la transaction. Malgré une telle sécurité cryptographique, cette personne ne peut-elle pas signer une transaction qu’elle a déjà passée ? Exemple : Alice a reçu dix Bitcoins dans le le but d’une transaction avec le numéro de transaction 1234. Elle peut très bien passer la même transaction 1234 et donner ces dix Bitcoins à Bob et Charlie. Puisqu’elle signera avec sa clé privée, ce qui signifie qu’il s’agit d’une transaction authentique, qu’est-ce qui, selon vous, peut l’empêcher de doubler ses dépenses? Notez qu’il n’y a aucun moyen dans Bitcoin qui vous permette d’empêcher de tenter de faire une double dépense, mais le système est conçu de sorte qu’une telle tentative ne sera pas couronnée de succès. La seule façon d’empêcher de telles tentatives est d’être au courant de toutes les transactions qui ont lieu. C’est pourquoi toutes les transactions en Bitcoin sont diffusées sur l’ensemble du réseau. Une fois qu’une transaction est passée, elle ne fait plus partie des UTXOs et un nouveau numéro de transaction est généré pour faire partie de l’UTXO, que seul le destinataire peut dépenser. C’est ainsi que les nœuds peuvent valider les transactions.

En outre, la seule façon d’éviter une attaque à double dépense est de connaître toutes les transactions. Lorsque vous êtes au courant de toutes les transactions, vous connaissez les dépenses et les UTXOs. Lorsqu’un nouveau bloc est proposé par un mineur, il est nécessaire que toutes les transactions dans le bloc soient valides. Cela signifie-t-il que le nœud proposant un bloc ne peut pas inclure une transaction non valide? La réponse est “Oui”. Ils peuvent certainement injecter une transaction frauduleuse, mais le reste des nœuds la rejettera. Le PoW que le nœud aurait fait (nous allons entrer dans les détails sous peu) en dépensant des ressources informatiques et de l’électricité serait en vain! Ainsi, un nœud ne voudrait jamais proposer un bloc invalide, grâce au consensus PoW.

Bien que n’ayant pas une notion de temps global, les transactions sont réalisées ensemble pour former un bloc qui devient une partie de la blockchain, plus de blocs sont ajoutés à la chaîne un à un, et il y a un ordre ! L’ordre dans lequel les transactions ont eu lieu est préservé par la blockchain. De cette façon, le consensus se produit au niveau du bloc, qui se propage tout le chemin aux transactions granulaires.

Nous savons maintenant que chaque nœud dans le réseau Bitcoin a sa propre copie de la blockchain, et il n’y a pas de “blockchain mondiale” en tant que telle ; c’est un réseau décentralisé après tout. Chaque nœud dans toutes ces copies de blockchains comprend de nombreuses transactions. Il est vrai que chaque nœud maintient une liste d’UTXOs et lorsqu’on leur donne une chance (un nœud est choisi au hasard, nous verrons comment) de proposer un bloc, ils comprennent autant de transactions que possible jusqu’à la limite de bloc de 1 Mo ou 2 Mo. Si le bloc réussit à atteindre la blockchain, ils sont supprimés de la liste des UTXOs. Chaque nœud peut avoir des listes de transactions en circulation différentes parce qu’il est possible que certaines transactions ne soient pas entendues par certains nœuds.

Il est temps de comprendre comment l’algorithme PoW fonctionne vraiment. Nous avons appris le champ cible de difficulté dans l’en-tête de chaque bloc. Chaque nœud tente de résoudre le puzzle cryptographique avec l’espoir d’avoir de la chance et de proposer un bloc. La raison pour laquelle ils sont si désespérés en proposant un bloc, c’est parce qu’ils obtiennent de grands avantages lorsque leur bloc proposé devient une partie de la blockchain. Chaque transaction qu’un individu effectue, elle peut mettre de côté des frais de transaction pour les mineurs. Nous savons que tous les nœuds maintiennent la liste des transactions qui ne font pas encore partie de la blockchain et quand ils ont la chance de proposer un bloc, ils prennent autant de transactions qu’ils le peuvent et forment un bloc. Il est évident qu’ils prendront toutes les transactions qui leur donneraient le bénéfice le plus élevé et laisseraient celles avec des frais de transaction minimum ou nul. Il peut prendre un certain temps pour les transactions avec de faibles frais de transaction pour entrer dans les blocs, et les chances sont moindres pour ceux qui n’ont pas de frais de transaction à tous. Outre les frais de transaction, les nœuds qui proposent un nouveau bloc sont récompensés par de nouveaux Bitcoins. Avec chaque bloc réussi, de nouveaux Bitcoins sont générés et le mineur qui a proposé le bloc obtient cela ; c’est la seule façon de créer de nouveaux Bitcoins dans le système Bitcoin. C’est ce qu’on appelle la « récompense de bloc ». Techniquement, le nœud qui propose un bloc comprend une transaction spéciale appelée « création de pièces » dans le bloc proposé où l’adresse du destinataire est celle que possède le mineur. Lorsque le Bitcoin a été lancé, la récompense de bloc était de 50 Bitcoins (BTC). Par la conception, il ne peut y avoir que 21.000.000 BTC au total, de sorte que la récompense de bloc est réduit de moitié tous les 210.000 blocs. Il a commencé à 50, puis il est devenu 25, puis 12,5, et il continue de cette façon jusqu’à un moment donné dans le temps (quand il atteint 21.000.000 BTCs) il tend vers zéro. Voici l’extrait de code de Bitcoin Core (main.cpp) qui montre ce processus de réduction de moitié :

int64_t GetBlockValue(int nHeight, int64_t nFees)

{

int64_t nSubsidy = 50 * COIN;

int halvings = nHeight / Params().SubsidyHalvingInterval();

// Forcer la récompense de bloc à zéro lorsque le décalage à droite n’est pas défini.

if (halvings >= 64)

return nFees;

// La subvention est réduite de moitié tous les 210 000 blocs, ce qui se produit environ tous les 4 ans.

nSubsidy >>= halvings;

return nSubsidy + nFees;

}

Notez dans l’extrait de code précédent comment la récompense de bloc est réduite de moitié. L’explication suivante donne une meilleure image de cette conception:

// Récompense de bloc réduite de moitié, reste à 50%

BlockReward = BlockReward >> 1;

// La récompense de bloc encore réduite de moitié, reste à 25%

BlockReward = BlockReward-(BlockReward>>2);

// La récompense de bloc encore réduite de moitié, reste à 12,5%

BlockReward = BlockReward – (BlockReward>>3);

Même si les récompenses semblent lucratives, il n’est pas si facile d’avoir de la chance et d’être le nœud qui arrive à proposer un bloc. Si vous n’êtes pas assez chanceux, tout le travail que vous avez fait serait en vain; c’est un inconvénient! Alors, qu’est-ce que les nœuds font en tant que PoW? Revenons au casse-tête de la difficulté maintenant. Chaque nœud minier travaille en tout temps à proposer un bloc, mais un seul réussit à un moment donné. Supposons qu’un bloc est déjà proposé, et maintenant tous les nœuds miniers travaillent à proposer un nouveau bloc. Passons par le processus étape par étape et comprenons l’ensemble du flux:

Étape 1 :

Les mineurs utilisent un logiciel pour suivre les transactions, éliminer ceux qui ont déjà fait un bloc réussi dans la blockchain, rejeter les transactions frauduleuses, et résoudre le puzzle cryptographique pour proposer un nouveau bloc et le relais à l’ensemble du réseau.

Le meilleur logiciel pour miner est le bitcoin officiel Core, mais il y a eu beaucoup d’autres variantes que les gens ont mis au jour. Si vous vous connectez à ce lien (https://bitcoin.org/ en/download) vous constaterez que le noyau officiel bitcoin est pris en charge dans Windows, Linux, Mac OS, Ubuntu et ARM Linux. Ainsi, quand nous disons que le nœud minier sélectionne toutes les transactions (peut-être celles qui donnent au mineur le bénéfice le plus élevé) jusqu’à la limite de bloc de 1 Mo (2 Mo pour Bitcoin Cash), ils hâtèrent également ces transactions et génèrent la racine de Merkle qui deviendrait une partie de l’en-tête de ce nouveau bloc. Cette racine de Merkle représente toutes les transactions.

Étape 2 :

Ils préparent l’en-tête du bloc. Mis à part le nonce, le reste est disponible à cette étape. C’est le travail du nœud minier de trouver le nonce en hachage l’en-tête de bloc deux fois et en le comparant à la cible de difficulté pour voir si elle est inférieure à cela. Ils continuent à changer le nonce jusqu’à ce qu’il satisfait cette condition, et il n’y a pas de raccourci pour trouver un nonce rapidement; il faut essayer toutes les options possibles. Nous avons déjà examiné comment calculer la cible difficile à l’aide des quatre octets de données présents dans l’en-tête lui-même, et nous avons appris comment il change toutes les deux semaines. Voir ce qui suit pour savoir à quoi ressemble ce processus :

H [ H (Version | Previous Block Hash | Merkle Root | Time Stamp

| Difficulty Target | Nonce) ]

< [ Difficulty Target ]

Étape 3 :

Le mineur continue de changer le champ de nonce à l’étape 2, en l’incrémentant par «1» jusqu’à ce qu’il satisfasse la condition, c’est un phénomène récursif. La cible de difficulté pour chaque nœud est le même et tous essaient de résoudre le même problème, mais n’oubliez pas qu’ils peuvent avoir différentes variantes de pools de transactions et donc la racine Merkle pour eux serait différente. Puisque chaque nœud essaie d’étendre la blockchain la plus longue et principale, de sorte que le hachage de bloc précédent soit le même.

Ainsi, le hachage Sha256 deux fois pour l’en-tête de bloc devrait être inférieur à la cible pour être en mesure de proposer le bloc à l’ensemble du réseau. Voir l’exemple suivant pour une meilleure compréhension:

Target : 0000000000000074cd00000000000000000000000000000000000000000000000

Hash : 0000000000000074cc4471deff052ced7f07347e4eda86c845a2fcf0553ed7f0

Notez que la valeur de hachage et la valeur cible ont le même nombre de zéros principaux (c.-à-d., 14) et « 74cc » est inférieure à « 74cd », de sorte qu’il satisfasse la condition et ce bloc peut alors être proposé. Dans de nombreux endroits, vous trouverez que cette explication est simplifiée avec des valeurs de base à la fois de la cible et le hachage, et comptant que les zéros de premier plan. Si le hachage a plus de zéros de tête que la cible, alors il satisfait la condition. Rappelez-vous encore que plus il y a de zéros dans la cible, plus il est difficile de trouver le hachage qui peut satisfaire la condition.

Connectons cet apprentissage jusqu’à présent avec la véritable implémentation Bitcoin. Nous savons que le temps de création de blocs est réglé à dix minutes , il est codé dans les binaires Bitcoin pour 2 016 blocs en deux semaines, comme nous l’avons déjà discuté, et ne change pas jusqu’à ce qu’une fourchette dure se produise. Vous pouvez parcourir les blocs proposés et voir les hachage qui ont satisfait la cible de difficulté sur le site https://blockchain.info et voir par vous-même que les hachages pour différents blocs aurait différents zéros de premier plan, juste pour définir le temps de création de bloc à dix minutes en moyenne. Dans les premiers jours, le nombre de zéros de premier plan était d’environ neuf ou dix, et aujourd’hui il est passé d’environ 18 à 20 zéros. Il peut augmenter encore plus au fur et à mesure que des nœuds informatiques plus puissants capables de plus de taux de hachage Réseau.

Étape 4 :

Une fois qu’un mineur trouve le bloc valide, il publie immédiatement le bloc sur l’ensemble du réseau. Chaque nœud qui reçoit ce bloc vérifie individuellement à nouveau si le mineur qui a proposé le bloc effectivement résolu le puzzle minier. Pour que ces nœuds valident cela, ce n’est qu’une étape, comme indiqué ci-dessous :

H [H (Version| PreviousBlock Hash | Merkle Root | Time Stamp |

Difficulty Target | Found Nonce)]

< [ Difficulty Target ]

Notez qu’ils utilisent simplement l’en-tête de bloc qui comprend le nonce trouvé par le mineur proposant pour voir si le hachage est inférieur à la cible et est valide. S’il s’agissait d’un nonce valide et de la condition remplie, alors ils vérifient les transactions individuelles proposées dans le bloc avec sa racine de Merkle dans l’en-tête de bloc. Si toutes les transactions sont valides, alors ils ajoutent ce bloc à la copie locale de leur blockchain. Ce nouveau bloc a la transaction de base de pièces qui génère de nouvelles pièces (il a commencé avec 50 BTC, puis 25, puis 12,5, et continue de réduire de moitié comme expliqué plus haut) comme une récompense pour le mineur qui a proposé le bloc valide.

Le minage de blocs n’est pas une tâche facile, il est rendu possible grâce à l’algorithme de minage PoW. Pour qu’un nœud propose un bloc invalide, il doit brûler beaucoup d’électricité et de cycles de processeur pour trouver le nonce et proposer le bloc qui serait finalement rejeté par les nœuds dans le réseau. S’il avait été une tâche aisée, de nombreux nœuds continueraient à essayer d’inonder le réseau avec de mauvais blocs. Vous devez comprendre et apprécier maintenant comment Bitcoin empêche de telles situations dans une manière théoricienne du jeu ! Il est toujours rentable pour les mineurs de jouer selon les règles et ils ne gagnent pas d’avantages supplémentaires en ne suivant pas les règles.

Dans les étapes précédentes, nous avons appris la procédure de minage par PoW qui est mise en œuvre dans Bitcoins. Une des meilleures choses dans cette conception est la sélection aléatoire d’un nœud à miner qui arrive à proposer un bloc. Personne ne sait qui aurait la chance de trouver le bon nonce et de proposer un bloc, c’est purement un phénomène aléatoire. Nous savons déjà que générer un vrai nombre aléatoire est assez difficile et c’est quelque chose qui est la surface d’attaque la plus vulnérable pour la plupart des implémentations cryptographiques. Avec un design tel que Bitcoin, la sélection aléatoire d’un nœud pour proposer un bloc vraiment aléatoire.

La meilleure chose dans le minage de bitcoin est la récompense de bloc. C’est quelque chose qu’un mineur qui propose avec succès un nouveau bloc obtient, en utilisant la transaction de base de pièces dans le même bloc. Les mineurs obtiennent également les frais de transaction associés à toutes les transactions qu’ils ont incluses dans le bloc. Ainsi, la récompense d’extraction pour un bloc est une combinaison de récompense de bloc et de frais de transaction comme indiqué ci-dessous :

Récompense minage = Récompense de bloc + Frais de transaction totaux de toutes les transactions dans le bloc

Nous savons que le minage est la seule façon de créer de nouveaux Bitcoins dans le système Bitcoin, mais est-ce là le but du minage ? non, ce n’est pas le but ! Le but du minage est d’exploiter de nouveaux blocs, et la génération de nouveaux Bitcoins et aussi les frais de transaction est d’encourager les mineurs de sorte que de plus en plus de mineurs sont intéressés par le minage pour faire fonctionner la blockchain.

Évidemment, pourquoi voudriez-vous faire du minage si vous ne gagnez pas d’argent ? Tout travail mérite salaire comme disait l’autre. C’est encore la théorie du jeu. Un mécanisme d’incitation approprié est la clé pour rendre un système décentralisé et autosuffisant. Le système Bitcoin n’a pas un moyen de pénaliser les nœuds qui ne jouent pas honnêtement, par contre il ne récompense que le comportement honnête. Les acteurs du réseau blockchain Bitcoin, tels que les individus qui utilisent simplement Bitcoin ou les mineurs, sont tous identifiés à l’aide de leurs clés publiques. Il est possible pour eux de générer autant de paires de clés que possible et cela en fait un système pseudonyme (basé sur le pseudo). Un nœud ne peut pas être identifié de façon unique avec sa clé publique qu’il a utilisée dans la transaction de base de coin, car dans l’instant suivant, il peut créer une nouvelle paire de clés et se présenter avec une nouvelle adresse réseau. Ainsi, l’incitation appropriée est la meilleure manière de s’assurer que les acteurs dans le système jouent honnêtement-encore une fois la beauté de la théorie de jeu !

Après la diffusion d’un bloc, disons qu’un nœud l’a vérifié, a trouvé le nonce et les transactions et tout le reste pour être valide, et l’a inclus dans sa copie locale de la blockchain. Cela signifie-t-il que les transactions qui étaient là dans le bloc sont toutes réglées et confirmées maintenant ?

Eh bien, pas vraiment ! Il y a une chance que deux blocs soient entrés en même temps et tandis qu’un nœud a commencé à étendre l’un d’eux, il y a une chance qu’une majorité des nœuds s’étendent sur l’autre bloc. Finalement, la plus longue blockchain devient la chaîne d’origine. Il s’agit d’un scénario où un bloc qui est absolument valide, avec toutes les transactions légitimes et une valeur de nonce appropriée qui a satisfait le puzzle minier, peut encore être abandonné par le réseau Bitcoin. Ces blocs qui ne deviennent pas une partie de la blockchain finale sont appelés blocs orphelins. Maintenant, cette explication indique qu’il y a une certaine possibilité d’un ou plusieurs blocs de devenir orphelin à tout moment.

Ainsi, la meilleure stratégie serait d’attendre jusqu’à ce que de nombreux blocs sont ajoutés à la chaîne. En d’autres termes, lorsqu’une transaction reçoit plusieurs confirmations, il est sûr de penser qu’elle fait partie de la chaîne de consensus final et qu’elle ne sera pas orpheline. Comme n’importe quel nombre de blocs sont ajoutés après un certain bloc, que de nombreux nombres de confirmations sont reçues par les transactions dans ce bloc. Bien qu’il n’y ait pas de règles en tant que telles qui définissent le nombre de confirmations que l’on devrait obtenir avant d’accepter une transaction, six confirmations ont été la meilleure pratique. Même avec quatre confirmations, il est tout à fait sûr de supposer qu’une transaction a été confirmée, mais six est la meilleure pratique parce qu’avec plus de confirmations, les chances d’un bloc de devenir orphelin diminue de façon exponentielle.

Propagation du bloc

Bitcoin utilise le minage PoW pour sélectionner au hasard un nœud qui peut proposer un bloc valide. Une fois que le mineur trouve un bloc valide, il diffuse ce bloc sur l’ensemble du réseau. La propagation du bloc dans le réseau se produit de la même manière que les transactions. Chaque nœud qui reçoit le nouveau bloc le diffuse de sorte que finalement le bloc atteint tous les nœuds dans le réseau. Veuillez noter qu’un nœud ne diffuse pas un bloc à moins qu’il ne fasse partie de la plus longue chaîne de son point de vue. Une fois que les nœuds reçoivent le nouveau bloc qui est proposé, ils vérifient non seulement l’en-tête et vérifient la valeur de hachage dans la plage acceptable, mais valident également chaque transaction qui a été incluse dans ce bloc. Il est clair maintenant que pour un nœud dans le réseau Bitcoin, la validation d’un bloc est un peu plus complexe par rapport à la validation des transactions. Comme pour les transactions, il est possible que deux blocs valides soient proposés en même temps. Dans un tel scénario, le nœud gardera les blocs et commencera à construire sur celui qui vient de la plus longue chaîne.

Nous devons comprendre qu’il y a toujours une latence pour qu’un bloc se propage à travers l’ensemble du réseau et atteigne tous les nœuds. La relation entre la taille du bloc et le temps pris est linéairement proportionnelle, en ce sens que pour chaque kB ajouté à la taille du bloc, la latence augmente linéairement. Il est évident qu’une telle latence réseau aurait un impact sur le taux de croissance de la blockchain. Une étude de mesure menée par Decker et Wattenhofer traite de cette situation. Reportez-vous à la figure 3-19, qui montre la relation entre la taille du bloc et le temps qu’il a fallu pour atteindre 25 % (ligne 1), 50 % (ligne 2) et 75 % (ligne 3) des nœuds surveillés.

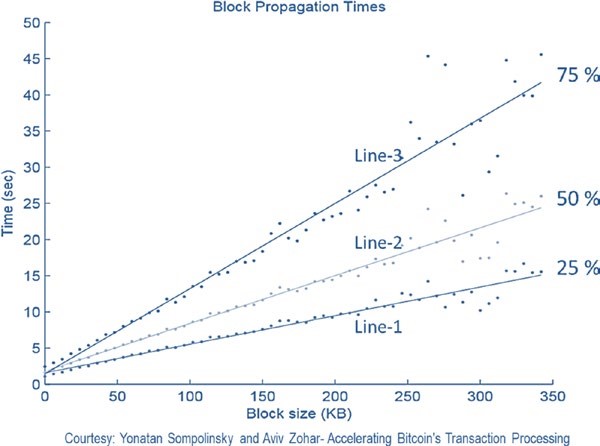
Figure 3-19. Temps de propagation de bloc en ce qui concerne la taille du bloc

La bande passante réseau est la principale raison de ces latences réseau et elle n’est jamais cohérente dans toutes les régions du globe. En plus de cela, nous savons que les paquets de diffusion de blocs passent par de nombreux sauts pour finalement atteindre tous les nœuds. Un bloc Bitcoin typique est de 1 Mo et la nouvelle variante de Bitcoin avec une fourchette dure qui est venu (Bitcoin Cash) est de taille de bloc de 2 Mo; vous pouvez imaginer les limitations inhérentes dues à la latence.

Selon la recherche sur le réseau, il y a plus d’un million de nœuds Bitcoin qui sont connectés au réseau Bitcoin en un mois et il y a des milliers de nœuds complets qui sont presque toujours connectés au réseau en permanence.

Mettre tout cela ensemble

À un niveau élevé, si nous venons de mettre les événements dans l’ordre, ils ont lieu, alors voici comment on peut les représenter :

• Toutes les nouvelles transactions sont diffusées sur tous les nœuds.
• Chaque nœud qui entend les nouvelles transactions les recueille dans un bloc.
• Chaque nœud de minage travaille à trouver un PoW difficile pour son bloc pour être en mesure de le proposer au réseau.
• Quand un nœud a de la chance et trouve un nonce correct au puzzle PoW, il diffuse le bloc à tous les nœuds.
• Les nœuds n’acceptent le bloc proposé que si le nonce et toutes les transactions qu’il y a sont valides et n’ont pas déjà été dépensés.
• Les nœuds du réseau Bitcoin expriment leur acceptation du bloc en travaillant à la création du bloc suivant dans la chaîne, en utilisant le hachage du bloc accepté comme le hachage précédent pour le nouveau bloc qu’ils veulent miner.

Bitcoin Scripts

Dans cette section, nous allons approfondir les constructions de programmation réelles qui font les transactions se produire. L’entrée et la sortie de toutes les transactions Bitcoin sont intégrées avec des scripts. Les scripts Bitcoin sont basés sur la pile (stack-based), que nous verrons sous peu, et sont évalués de gauche à droite. Les scripts Bitcoin ne sont pas complets de Turing, donc vous ne pouvez pas vraiment faire tout et tout ce qui est possible à travers d’autres Turing-complete langages tels que C, C ++ ou Java, etc. Il n’y a pas de concepts de boucles dans le script Bitcoin, d’où le temps d’exécution pour les scripts n’est pas variable et est proportionnelle au nombre d’instructions. Cela signifie que les scripts s’exécutent dans un laps de temps limité et il n’y a aucune possibilité pour eux de rester coincés à l’intérieur d’une boucle. Aussi, le plus important, les scripts se terminent définitivement. Maintenant que nous en savons un peu plus sur les scripts, où s’exécutent-ils? Chaque fois que des transactions sont effectuées, que ce soit sur le plan programmatique, ou par l’intermédiaire d’un logiciel de portefeuille ou de tout autre programme, les scripts sont injectés à l’intérieur des transactions et c’est le travail des mineurs d’exécuter ces scripts pendant le minage. Le but des scripts Bitcoin est de permettre aux nœuds réseau de s’assurer que les fonds disponibles sont réclamés et dépensés uniquement par les parties ayant droit qui les possèdent vraiment.

Les transactions Bitcoin revisitées

Une transaction dans le réseau Bitcoin est un transfert de valeur, qui est une diffusion à l’ensemble du réseau et se retrouve dans un bloc dans la blockchain. Typiquement, il semble que les Bitcoins sont transférés d’un compte ou d’un portefeuille à un autre, mais en réalité, il est d’une transaction à l’autre.

Eh bien, avant d’entrer dans plus de détails, gardez à l’esprit que les adresses Bitcoin sont essentiellement la sortie à double hachage de la clé publique des participants.

La clé publique est d’abord hachée à l’aide de SHA256, puis par des algorithmes de hachage RIPEMD160, respectivement, pour générer des adresses Bitcoin de 160 bits. Nous avons déjà couvert ces techniques de hachages dans le chapitre précédent. Zoomons un peu plus sur les transactions maintenant. Jetez un oeil à l’arbre de transaction suivant (figure 3-20), la façon dont il se produit en Bitcoin.

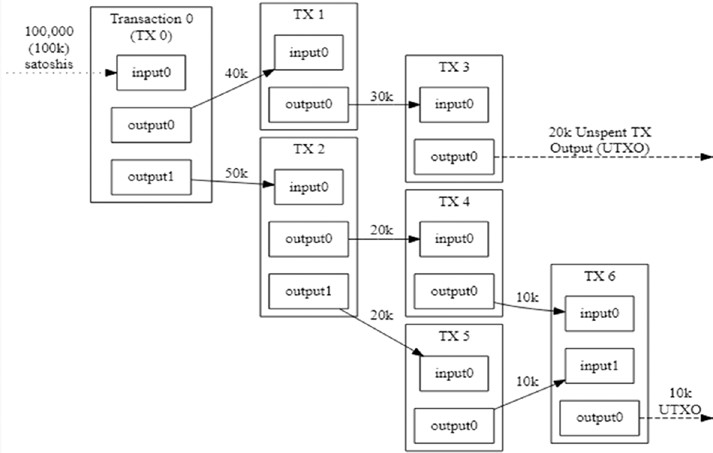
Figure 3-20. Une structure de transaction Bitcoin typique

Observez que la production des transactions précédentes devient entrée à de nouvelles transactions et ce processus se poursuit indéfiniment. Dans le chiffre précédent, si c’était vous qui avez obtenu le 100K de certaines sorties précédentes, il est devenu l’entrée dépensable à une nouvelle transaction. Notez que dans Tx 0, vous avez dépensé 40K et 50K et payé ces montants, et le montant restant (10K) est transformé en frais pour le mineur. Par défaut, le montant restant est versé au mineur, vous devez donc faire attention à ne pas ignorer de telles situations, ce qui est toujours le cas. Dans cette même situation, sur le montant restant de 10K, vous pouvez transférer dire 9K à votre propre adresse et laisser de côté 1K pour les frais de minage. Lorsqu’un montant n’est pas dépensé, en ce sens qu’une transaction n’est pas utilisée comme entrée dans une nouvelle transaction, il reste un UTXO, qui peut être dépensé plus tard. De toute évidence, ceux qui ont déjà été dépensés. Ainsi, tous les UTXOs combinés pour tous les comptes (clés publiques) que vous détenez sont votre solde de portefeuille.

Faites une pause ici, et réfléchissez à la façon dont il a dû être programmé. N’oubliez pas que les entrées et les sorties des transactions sont équipées de scripts pertinents pour le rendre possible. Ce n’est qu’à travers les scripts qu’il peut être assuré que vous êtes l’utilisateur autorisé à effectuer une transaction et que vous avez le montant nécessaire que vous avez reçu d’une transaction précédente. Cela signifie que les entrées et les sorties sont tout aussi importantes. Voici l’apparence du contenu de la transaction :

Sortie de transaction – Nombre de Bitcoins à transférer et Sortie

Script

Entrée de transaction – Référence à la sortie de transaction précédente

Script d’entrée

Que ce soit pour examiner le script de sortie d’abord ou le script d’entrée d’abord est en fait un problème d’œuf-poule. Mais nous verrons le script de sortie d’abord parce que c’est celui qui est consommé par le script d’entrée de la prochaine transaction. Répétons et obtenons ce droit, que tout en faisant une transaction, le script de sortie de la transaction en cours est là juste pour activer la transaction future qui peut consommer cela comme entrée, mais pour cette transaction en cours, c’est le script de sortie de la transaction précédente qui vous permet de le dépenser. C’est pourquoi les scripts de sortie ont la clé publique du destinataire et la valeur (montant des Bitcoins) transférée. Lorsque les scripts de sortie sont utilisés comme entrées, leur but principal est de vérifier la signature par rapport à la clé publique. Les scripts de sortie sont également appelés ScriptPubKey. À moins que cette sortie ne soit dépensée, il reste un UTXO en attente d’être dépensé.

Le script d’entrée dans la structure de données d’entrée de transaction a le mécanisme permettant de consommer la transaction précédente que vous essayez de dépenser. Il doit donc faire référence à cette transaction précédente. Le hachage de la transaction précédente et le numéro d’index « hachage, index » identifie l’endroit exact où vous avez reçu le montant que vous dépensez maintenant. Le but de l’« indice » est d’identifier la sortie prévue dans la transaction précédente. Si vous avez été le destinataire de la transaction précédente, vous devez fournir votre signature pour prétendre que vous êtes le propriétaire légitime de la clé publique à laquelle la transaction a été effectuée. Cela vous permettra de dépenser cette transaction. En outre, vous devez fournir votre clé publique, qui hacha à celui utilisé comme adresse de destination dans la transaction précédente. Les scripts d’entrée sont également connus sous le nom de ScriptSigs. L’objectif ultime du script est de pousser les signatures et les clés sur la pile.

Une transaction Bitcoin typique a les champs suivants (tableau 3-5).

Tableau 3-5. Champs de transactions Bitcoin

Champ	Taille	Description
Version no	4 octets	Actuellement 1. il indique aux pairs bitcoins et aux mineurs qui ont établi des règles à utiliser pour valider cette transaction.
In-Counter	1 – 9 octets	l’entierceur positif (Vi = Varint). il indique lenombre total d’entrées.
Liste des entrées	Longueur De Variable	il répertorie toutes les entrées pour une transaction.
Out_counter	1 – 9 octets	l’intégrateur positif (Vi et Varint). il indique lenombre total de sorties.
liste des sorties lock_time	Longueur variable 4 octets	il répertorie toutes les sorties d’une transaction n’est pas utilisé actuellement. il indique si la transaction doit être incluse dans le bloc blockchain immédiatement après qu’elle a été validée par le mineur ou s’il devrait y avoir un certain temps de verrouillage avant qu’elle ne soit incluse dans le bloc.

Examinons maintenant une représentation différente de la même structure de transaction dont nous avons discuté dans la section précédente. Il s’agit de voir une vue plus détaillée de la structure de la transaction et des différentes composantes de celle-ci. Maintenant, consultez la figure 3-21.

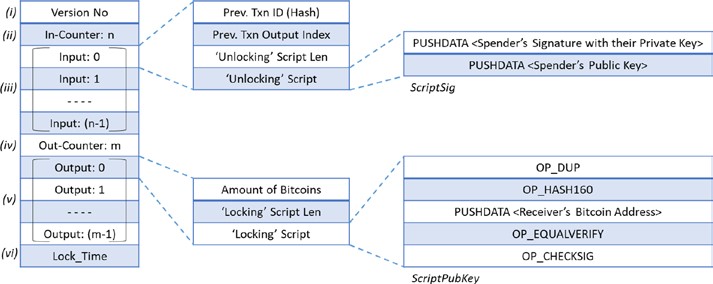
Figure 3-21. Composants granulaires d’une transaction Bitcoin

Comme vous pouvez le voir dans le chiffre précédent, les éléments de données tels que les signatures ou les clés publiques sont tous intégrés dans les scripts et font partie de la transaction. Juste en regardant les composants granulaires des transactions Bitcoin, beaucoup de vos requêtes seraient répondues à l’avance. Les instructions dans le script sont poussés sur la pile et exécutés, nous allons explorer en détail sous peu.

Lorsque les nœuds Bitcoin reçoivent les diffusions de transaction, ils valident toutes ces transactions individuellement, en combinant le script de sortie de la transaction précédente avec le script d’entrée de la transaction en cours suivant les étapes mentionnées comme suit :

• Trouvez la transaction précédente dont la sortie est utilisée comme entrée pour effectuer cette transaction. Le champ “Prev. Txn ID (Hachage)” contient le hachage de cette transaction précédente.
• Dans la sortie de transaction précédente, trouvez l’indice exact où le montant a été reçu. Il peut y avoir plusieurs récepteurs dans une transaction, de sorte que l’index est utilisé pour identifier l’initiateur de cette transaction en cours dont l’adresse a été utilisée comme destinataire dans la transaction précédente.
• Consommez le script de sortie utilisé dans la transaction précédente à l’aide du script de déverrouillage appelé «ScriptSig». Notez à la figure 3-21 qu’il y a devant elle un champ qui spécifie la longueur de ce script de déverrouillage.
• Joignez-vous à ce script de sortie avec le script d’entrée en l’appliquant simplement pour former le script de validation et exécutez ce script de validation (rappelez-vous qu’il s’agit d’un langage de script basé sur la pile).
• La valeur du montant est en fait présente dans le script de sortie, c’est-à-dire, le «ScriptPubKey». C’est le script de verrouillage qui verrouille la sortie de transaction avec les conditions de dépense et garantit que seul le propriétaire légitime de l’adresse Bitcoin à laquelle cette transaction a été faite peut plus tard la réclamer. Observez qu’il a également le champ de longueur de script de verrouillage juste avant lui. Pour la transaction en cours, ce script de sortie est uniquement pour l’information, et joue son rôle à l’avenir lorsque le propriétaire tente de le dépenser.
• C’est le script de validation qui décide si l’entrée de transaction en cours a le droit de dépenser l’UTXO précédent en validant les signatures. Si le script de validation s’exécute avec succès, il est confirmé que la transaction est valide et que la transaction a été conclue.

Examinons l’explication précédente à travers une représentation schématique pour obtenir une meilleure compréhension. Supposons qu’Alice paie Bob, disons, cinq BTC. Cela signifie qu’Alice avait reçu 5BTC dans l’une des transactions précédentes qui a été verrouillées en utilisant ScriptPubKey. Alice peut prétendre qu’elle est la propriétaire légitime de cette transaction en la déverrouillant avec ScriptSig et peut la dépenser à Bob. De même, maintenant, si Bob essaie de passer trois BTC à Charlie et deux BTC à lui-même, alors voici à quoi elle ressemblerait (figure 3- 22).

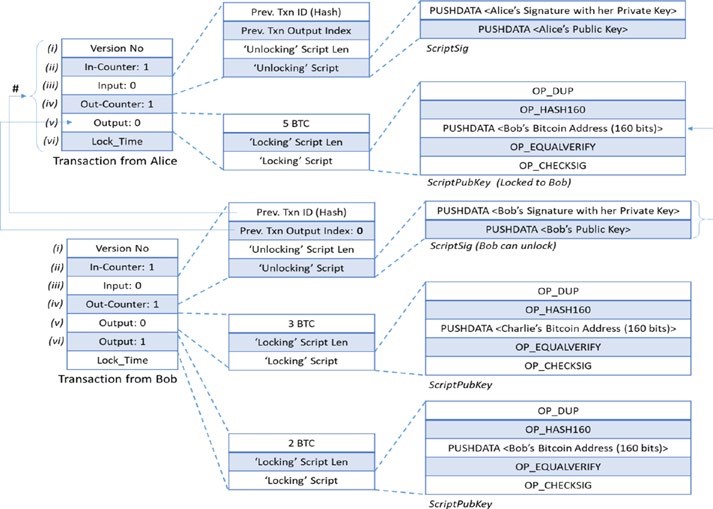
Figure 3-22. Un exemple pratique de scripts Bitcoin

Lorsque le réseau Bitcoin, plus précisément les mineurs, reçoivent la transaction d’Alice, ils vérifient et confirment qu’il s’agit d’une transaction valide et l’approuvent en l’incluant dans leurs blocs (enfin, celui qui propose un bloc le fait). Lorsque cela se produit, la sortie de cette transaction devient une partie de l’UTXO au nom de Bob, qui pourrait plus tard la dépenser. Et c’est ce qui se passe dans notre exemple, que Bob la dépense aussi pour Charlie. Bob l’a fait en consommant la transaction précédente, en la déverrouillant avec sa signature et sa clé publique, pour prouver qu’il est le propriétaire de l’adresse Bitcoin qu’Alice avait utilisée. Observez qu’il y a deux sorties dans la transaction de Bob.

Comme il avait reçu cinq BTC d’Alice et paie trois BTC à Charlie, il doit transférer le reste à lui-même afin qu’elle devienne deux BTC d’UTXO liée à Bob lui-même et il pourrait la dépenser à l’avenir. Dans la transaction de Bob, les trois BTC à Charlie sont verrouillés en utilisant le script de verrouillage pour que Charlie puisse la dépenser plus tard.

Pensez-vous maintenant à la façon dont les scripts sont combinés et exécutés ensemble? N’oubliez pas que le script de déverrouillage de la transaction en cours est exécuté avec le script de verrouillage de la transaction précédente. Comme nous l’avons déjà dit, l’exécution des scripts est le travail d’un mineur et ils ne se produisent pas au logiciel de portefeuille. Dans l’exemple précédent, lorsque Bob effectue les transactions, les mineurs exécutent le script de déverrouillage ScriptSig de la transaction de Bob, puis exécutent immédiatement le script de verrouillage ScriptPubKey de la transaction d’Alice dans l’ordre. Si l’exécution séquentielle d’une manière basée sur la pile pour le script de validation combiné s’exécute avec succès en retournant TRUE, alors la transaction de Bob est exceptée par tous les nœuds qui la valident. Nous allons jeter un oeil aux scripts Bitcoin et comment une machine virtuelle de script Bitcoin exécute la pile lors de l’exécution des commandes de script combinées plus en détail dans la section suivante. Dans cette section, cependant, jetez un oeil à l’exemple suivant qui représente la transaction du point de vue d’un développeur:

Exemple de code avec une seule entrée et une sortie

{

“hash”: “a320ba8bbe163f26cafb2092306c153f87c1c2609b25db0 c13664ae1afca78ce”,

“ver”: 1,

“vin_sz”: 1,

“vout_sz”: 1,

“lock_time”: 0,

“size”: 51,

“in”:[

{

“prev_out”:

“hash”:”83cd5e9b704c0a4cb6066e3a1642b483adc8f73a76791c82a73dfa381281d32f”,

“n”:0

},

“scriptSig”:”63883d3d2dea35029d17d25b8a926675def0045c397d3df55b0ae145ef80db7849599b930220ab13bd2dda2ca0a67e2c5cd28030bb9b7b3dcacf176652dac82fe9d5873f3409661281d32f6d35b46906c5566c562bf8b48f4f938c077bcb29d46b0560fa5c61813d3d2d”

}

],

“out”:[

{

“value”:”0.08″,

“scriptPubKey”:”OP_DUP OP_HASH160 b3a2c0d84ec82cff932b5c3231567a0d48ab4c78

OP_EQUALVERIFY OP_CHECKSIG”

}

]

}

Les transactions Bitcoin ne sont pas cryptées, il est donc possible de parcourir et de visualiser toutes les transactions jamais collectées en blocs.

Scripts

Un script est en fait une liste d’instructions enregistrées à chaque transaction qui décrit comment la prochaine personne peut accéder à ces Bitcoins reçus et les dépenser. Bitcoin utilise un langage de script non-Turing-complet basé sur la pile où les instructions sont traitées de gauche à droite. Gardez à l’esprit qu’il n’est pas-Turing-complet par la conception!

Nous avons examiné les scripts d’entrée et de sortie dans la section précédente. Nous sommes maintenant conscients que le script d’entrée ScriptSig est le script de déverrouillage et a deux composants, la clé publique et la signature. La clé publique est utilisée parce qu’elle s’adresse à l’adresse Bitcoin à laquelle la transaction a été dépensée, lors de la transaction précédente. L’objectif de la signature numérique ECDSA est de prouver la propriété de la clé publique, d’où l’adresse Bitcoin pour être en mesure de le dépenser davantage. De même, le script de sortie ScriptPubKey dans la transaction précédente était de verrouiller la transaction au propriétaire légitime de l’adresse Bitcoin. Ces deux scripts, ScriptSig de la transaction en cours et ScriptPubKey de la transaction précédente, sont combinés et exécutés. Jetez un coup d’œil à son apparence après leur combinaison (figure 3-23).

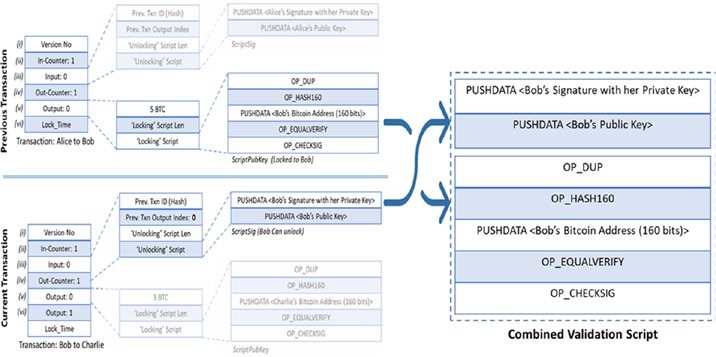
Figure 3-23. Formation de script de validation combiné

Comme nous l’avons déjà appris, il est important de noter que le script Bitcoin soit fonctionne avec succès ou il échoue. Lorsque les transactions sont valides, elles s’exécutent avec succès sans aucune erreur. Bitcoin scripting language est une version très simplifiée des langages de programmation et est assez petite, avec seulement 256 instructions au total. Sur ces 256, 15 sont désactivés et 75 sont réservés peut-être pour une utilisation ultérieure. Ces instructions de base comprennent des instructions mathématiques, logiques (si/alors), des rapports d’erreur et des instructions de retour. En dehors de ceux-ci, il y a quelques instructions cryptographiques supplémentaires telles que le hachage, la vérification de signature, etc. Nous n’entrerons pas dans tous les ensembles d’instructions disponibles, et nous nous concentrerons uniquement sur ceux que nous utiliserons dans ce chapitre. Voici quelques-uns :

• OP_DUP: Il ne fait que dupliquer l’élément supérieur de la pile.
• OP_HASH160: Il s’empare deux fois, d’abord avec SHA256 puis RIPEMD160.
• OP_EQUALVERIFY: Il retourne VRAI si les entrées sont appariées, et FALSE autrement et marque la transaction invalide.
• OP_CHECKSIG: Vérifie si la signature d’entrée est une signature valide à l’aide de la clé publique elle-même pour le haussier de la transaction en cours.

Pour exécuter ces instructions, nous avons juste à pousser ces instructions sur la pile, puis les exécuter. Mis à part la mémoire que la pile prend, il n’y a pas de mémoire supplémentaire nécessaire et cela rend les scripts Bitcoin efficace. Comme vous l’avez vu, il y a deux types d’instructions dans le script, l’une est l’instruction de données et l’autre est l’opération de codes. Les entrées précédentes de liste sont toutes des opérations de codes, et le script de validation combiné que nous avons vu avant a deux de ces types d’instructions. Les instructions de données sont juste pour pousser les données sur la pile et pas vraiment pour effectuer une fonction, et le seul but des opérations de codes est d’exécuter certaines fonctions sur les données dans la pile et sortir le cas échéant. Discutons de la façon dont la transaction de Bob serait exécutée avec une telle implémentation basée sur la pile. Repensez le script combiné où Bob essaie de passer une transaction déjà reçue dans la transaction en cours à Charlie (figure 3-24).

Figure 3-24. Script combiné de ScriptPubKey et CheckSig

La mise en œuvre correspondante basée sur les piles serait la suivante (figure 3-25).

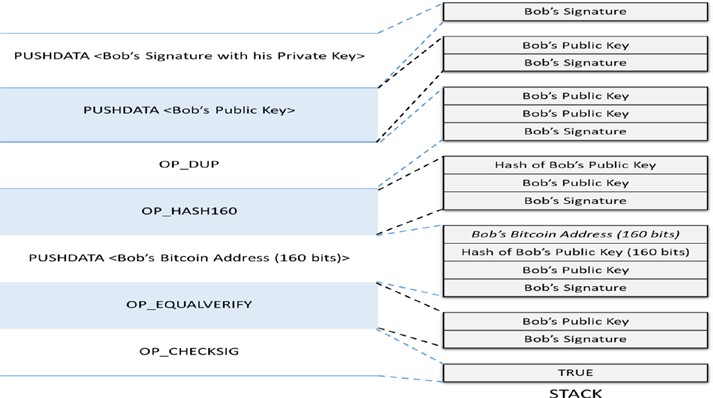
Figure 3-25. Exemple d’implémentation basée sur la pile du script Bitcoin

Bien que la précédente implémentation basée sur la pile est explicite, nous allons rapidement passer en revue ce qui s’est passé ici.

• Tout d’abord a été l’instruction de données signature de Bob et a donc été poussé sur la pile
• Puis a été sa clé publique à nouveau une instruction de données et a été poussé sur la pile
• Puis c’était OP_DUP, un opcode. Il reproduit le premier élément de la pile, de sorte que la clé publique de Bob a été dupliqué et est devenu le troisième élément sur la pile.
• Ensuite, il y a eu OP_HASH160, un Opcode, qui a hashed la clé publique de Bob deux fois, une fois avec SHA256, puis avec RIPEMD160, et la sortie finale de 160 bits a remplacé la clé publique de Bob et est devenu le haut de la pile.
• Ensuite, c’est l’adresse Bitcoin de Bob (160 bits) une instruction de données, qui a été poussé à la pile.
• Suivant était un opcode, OP_EQUALVERIFY, qui vérifie les deux premiers éléments de la pile et si elles correspondent, il les apparaît à la fois une erreur est lancée et le script se terminerait.
• Puis a été à nouveau un OP_CHECKSIG opcode, qui

vérifie la clé publique par rapport à la signature pour valider l’authenticité du propriétaire. Cet opcode est également capable de consommer les deux entrées et de les faire sauter de la pile.

Vous devez vous demander ce que si quelqu’un tente d’injecter des scripts frauduleux ou tente de les utiliser à mauvais escient. Veuillez noter que les scripts Bitcoin sont standardisés et que les mineurs en sont conscients. Tout ce qui ne suit pas la norme est abandonné par les mineurs, car ils ne perdaient pas leur temps à exécuter de telles transactions.

Noeuds complets vs SPV

Nous avons déjà un heads-up sur les nœuds complets et SPV dans ce chapitre. Il est évident que la notion de nœud complet et de nœud léger est mise en œuvre pour faciliter l’utilisation des Bitcoins et les rendre plus adaptables. Dans cette section, nous allons zoomer sur les détails techniques de ces variantes et comprendre leur but.

Nœuds complets

Les nœuds complets sont les composants les plus intégrals d’un réseau Bitcoin. Ce sont eux qui maintiennent et exécutent Bitcoin à partir de divers endroits à travers le monde. Comme nous l’avons déjà vu, téléchargez l’ensemble de la blockchain avec toutes les transactions, à partir du bloc de genèse au dernier bloc découvert. Le dernier bloc définit la hauteur de la blockchain.

Les nœuds complets sont extrêmement sûrs parce qu’ils ont toute la chaîne. Pour qu’un adversaire réussisse à tricher un nœud, une blockchain alternative doit être présentée, ce qui est pratiquement impossible. La vraie chaîne est la chaîne PoW la plus cumulative, et il devient informatiquement impossible de proposer un nouveau bloc frauduleux. Si toutes les transactions ne sont pas valides dans un bloc, le minage PoW effectuée par le concurrent sera vaine, parce que les autres mineurs n’iront pas miner à la suite de ce bloc. Un tel bloc devient orphelin assez tôt. Les nœuds complets construisent et maintiennent leur propre copie de la blockchain localement. Ils ne se fient pas au réseau pour la validation des transactions parce qu’ils sont autosuffisants. Ils sont simplement intéressés à connaître les nouveaux blocs qui sont proposés par d’autres nœuds afin qu’ils puissent mettre à jour leur copie locale après validation des blocs. Ainsi, nous avons appris que chaque nœud complet doit traiter toutes les transactions ; ils doivent stocker l’ensemble de la base de données, chaque transaction qui est actuellement diffusée, chaque transaction qui est jamais dépensée, et la liste des UTXOs; participera à la maintenance de l’ensemble du réseau Bitcoin; et ils doivent également servir les clients SPV.

Notez qu’il existe tellement de variétés de logiciels Bitcoin que les nœuds complets utilisent qui sont très différents dans l’architecture logicielle et programmés dans différentes constructions linguistiques. Cependant, le logiciel le plus largement utilisé est le logiciel “Bitcoin Core”; plus des trois quarts du réseau l’utilise.

SPV

La conception bitcoin a ce concept de simple vérification de paiement (SPV) des nœuds qui peuvent être utilisés pour vérifier les transactions sans exécuter les nœuds complets. Le fonctionnement des SPV est qu’ils ne téléchargent que l’en-tête de tous les blocs lors de la synchronisation initiale vers le réseau Bitcoin. Dans Bitcoin, les en-têtes de bloc sont de 80 octets chacun, et le téléchargement de tous les en-têtes n’est pas une grosse quantité et comporte quelques MBs au total.

Le but des SPV est de fournir un mécanisme pour vérifier qu’une transaction particulière était dans un bloc dans une blockchain sans nécessiter l’ensemble des données de la blockchain. Chaque en-tête de bloc a la racine de Merkle, qui est le hachage de bloc. Nous savons que chaque transaction a un hachage et que le hachage de transaction peut être lié au hachage de bloc en utilisant la preuve d’arbre de Merkle que nous avons discuté dans le chapitre précédent. Toutes les transactions dans un bloc forment les feuilles de Merkle et le hachage de bloc forme la racine de Merkle. La beauté de l’arbre Merkle est que seule une petite partie du bloc est nécessaire pour prouver qu’une transaction était en fait une partie du bloc. Donc, pour confirmer une transaction un SPV fait deux choses. Tout d’abord, il vérifie la preuve de l’arbre Merkle pour une transaction pour s’assurer qu’il s’agit d’une partie du bloc et deuxièmement, si ce bloc est une partie de la chaîne principale ou non; et il devrait y avoir au moins six blocs de plus créés après qu’il confirme qu’il est une partie de la plus longue chaîne. La figure 3-26 illustre ce processus.

Figure 3-26. Racine de Merkle dans l’en-tête de bloc de SPV

Approfondissons la technicité de la façon dont les SPV fonctionnent réellement dans la vérification des transactions. À un niveau élevé, il prend les mesures suivantes :

• Pour les pairs un SPV est connecté, il établit des filtres Bloom avec beaucoup d’entre eux et idéalement pas seulement à un pair, parce qu’il pourrait y avoir une chance pour ce pair d’effectuer le déni de service ou de tricher. Le but des filtres Bloom est de ne faire correspondre que les transactions qui intéressent un SPV, et non le reste dans un bloc sans révéler les adresses ou les clés qui intéressent le SPV.
• Les pairs renvoient les transactions pertinentes dans un message merkleblock qui contient la racine merkle et le chemin Merkle vers la transaction d’intérêt comme indiqué dans la figure ci-dessus. Le message merkleblock est de quelques kB et assez efficace.
• Il est alors facile pour les SPV de vérifier si une transaction appartient vraiment à un bloc de la blockchain.
• Une fois que la transaction est vérifiée, l’étape suivante consiste à vérifier si ce bloc fait réellement partie de la véritable blockchain la plus longue.

Ce qui suit (figure 3-27) représente cette communication SPV avec ses pairs.

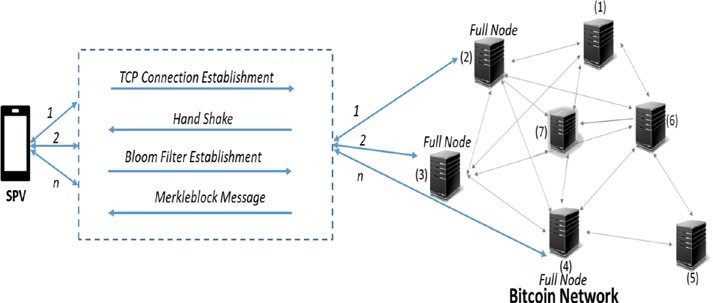
Figure 3-27. Mécanisme de communication SPV avec le réseau Bitcoin

Portefeuilles Bitcoin

Les portefeuilles Bitcoin sont très similaires au portefeuille que vous utilisez dans votre vie quotidienne, dans le sens où vous y avez accès et que vous pouvez dépenser quand vous le souhaitez. Les portefeuilles Bitcoin, cependant, sont un phénomène numérique. Je me souviens de l’exemple que nous avons utilisé dans la section précédente, où Alice a versé un certain montant à Bob. Comment le ferait-elle si Bob n’avait pas de compte ? Dans le paramètre Bitcoin, les comptes ou portefeuilles sont représentés par l’adresse Bitcoin. Bob doit d’abord générer une paire clé (clés privées/publiques). Bitcoin utilise l’algorithme ECDSA avec la courbe secp256k1 (ne vous inquiétez pas, c’est juste le type de courbe, une recommandation standard). D’abord une chaîne de bits aléatoires est générée pour servir de clé privée, qui est ensuite déterministe transformé en clé publique. Comme nous l’avons appris précédemment dans le chapitre 2, les clés privées/publiques sont mathématiquement liées et la clé publique peut être générée à partir de la clé privée à tout moment (déterministe). Donc, ce n’est pas vraiment une exigence pour sauver les clés publiques. en tant que tel. Le véritable hasard n’est pas possible grâce aux implémentations logicielles, de sorte que de nombreux serveurs ou applications utilisent des modules de sécurité matérielle (HSM) pour générer de véritables bits aléatoires et aussi pour protéger les clés privées. Contrairement aux clés publiques, les clés privées exigent absolument de les enregistrer avec une sécurité maximale. Si vous les perdez, vous ne pouvez pas générer une signature qui justifierait la propriété de la clé publique (ou adresse Bitcoin) qui a reçu un certain montant dans n’importe quelle transaction. Les clés publiques sont hachées deux fois pour générer l’adresse Bitcoin, d’abord avec SHA256, puis avec RIPEMD160. C’est aussi déterministe, donc étant donné une clé publique, il est juste une question de quelques hachage pour générer l’adresse Bitcoin.

L’adresse Bitcoin ne révèle pas vraiment la clé publique. C’est parce que les adresses sont des clés publiques à double hachage et il est tout à fait impossible de trouver la clé publique étant donné l’adresse Bitcoin. Cependant, pour quelqu’un avec une clé publique, il est facile de revendiquer la propriété d’une adresse Bitcoin. La technique de hachage dans Bitcoin raccourcit et obscurcit la clé publique. Bien qu’il facilite la transcription manuelle, il assure également la sécurité contre les problèmes imprévus qui pourraient permettre la reconstruction des clés privées de la clé publiques. C’est peut-être la mise en œuvre la plus sûre! Les clés publiques ne sont révélées que lorsque la sortie de transaction est réclamée par le propriétaire, et non lorsqu’elle leur a été transigée, comme vous pouvez le voir à la figure 3-28.

Figure 3-28. Révéler la clé publique pour réclamer une transaction

Les portefeuilles Bitcoin ne sont rien d’autre que les SPV et sont servis par les nœuds complets. Nous avons déjà examiné le fonctionnement des VCS, alors dans cette section, nous allons examiner certaines activités propres au portefeuille. Nous comprenons tous que pour faire une transaction, ou pour recevoir une transaction, vous n’avez pas besoin d’exécuter un nœud complet. Tout ce que vous voulez, c’est un portefeuille pour être en mesure d’enregistrer votre paire de clés privées / publiques, pour être en mesure de faire et de recevoir des transactions (en fait voir et vérifier ceux qui vous sont faits). Nous avons déjà appris la partie de vérification en passant par la section SPV. Jetons un coup d’oeil à la façon d’initier une transaction à l’aide d’un portefeuille.

Il est conseillé d’exécuter votre propre nœud complet et de connecter votre portefeuille à celui-ci, car ce serait le moyen le plus sécurisé de travailler sur Bitcoin. Cependant, ce n’est pas un mandat et vous pouvez toujours travailler sans maintenir votre propre nœud. Gardez à l’esprit que lorsque vous interrogez un nœud, vous devez mentionner votre adresse publique pour obtenir la liste des UTXOs, et le nœud complet est de plus en plus au courant de votre adresse publique, qui est une fuite de la vie privée! Tout ce qu’un portefeuille a à faire est d’obtenir la liste des UTXOs afin qu’il puisse passer une transaction en la signant avec sa clé privée et de publier cette transaction dans le réseau Bitcoin. Cela peut être fait en créant votre propre logiciel de portefeuille ou en utilisant un service de portefeuille tiers. Cependant, soyez prudent avec les fournisseurs de services de portefeuille parce que vous leur permettez de prendre le contrôle de votre clé privée. Qu’ils prennent délibérément vos Bitcoins ou qu’ils soient eux-mêmes piratés, ce qui a été le cas avec de nombreux services de portefeuille, vous perdez vos Bitcoins. En fin de compte, tous les fournisseurs de services de portefeuille sont centralisés, bien que le réseau Bitcoin soit décentralisé. Une représentation picturale typique de l’introduction d’une transaction Bitcoin par le biais du logiciel de portefeuille peut être représentée comme indiqué dans ce qui suit (figure 3-29).

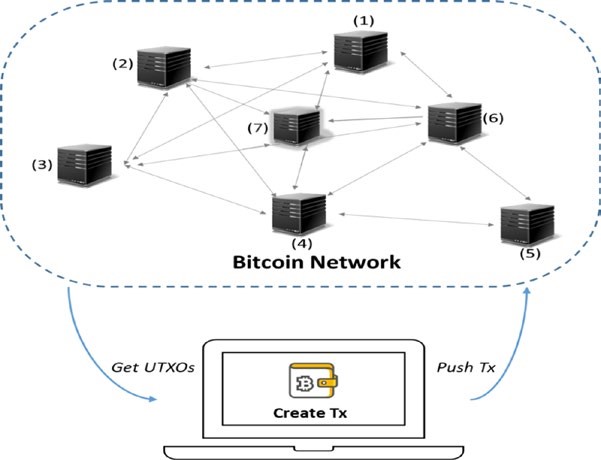
Figure 3-29. Une application portefeuille interagissant avec le réseau Bitcoin

Un exemple d’un client SPV qui peut servir de portefeuille Bitcoin est “BitcoinJ”. BitcoinJ est en fait une bibliothèque pour travailler avec le protocole Bitcoin, maintenir un portefeuille, et initier /valider des transactions. Il ne nécessite pas un nœud complet tel qu’un nœud Bitcoin Core localement et peut fonctionner comme un nœud client mince. Bien qu’il soit implémenté en Java, il peut être utilisé à partir de n’importe quel langage compatible JVM comme JavaScript et Python.

Résumé

Dans ce chapitre, nous avons appris comment les concepts de blockchain dont nous avons discuté dans le chapitre précédent ont été mis en place pour construire Bitcoin comme un cas d’utilisation de crypto-monnaie de la technologie blockchain. Nous avons couvert l’évolution de Bitcoin, l’histoire de celui-ci, ce qu’il est, les avantages de conception, et pourquoi il est si important. Nous avons appris à connaître les détails granulaires sur le réseau Bitcoin, les transactions, les blocs, la blockchain, le consensus, et comment tous ces éléments sont imbriqués ensemble. Ensuite, nous avons appris l’exigence d’une solution de portefeuille pour interagir avec le système blockchain Bitcoin.

Dans les années 1990, l’adoption massive d’Internet a changé la façon dont les gens faisaient des affaires. Il a éliminé la friction de la création et de la distribution de l’information. Cela a ouvert la voie à de nouveaux marchés, plus d’opportunités et de possibilités. De même, la blockchain est ici aujourd’hui pour porter l’Internet à un tout autre niveau. Bitcoin n’est qu’une application crypto-monnaie de la blockchain, et les possibilités sont illimitées. Dans le chapitre suivant, nous allons apprendre comment il est devenu une norme de facto pour diverses applications décentralisées sur un réseau public blockchain.

CHAPITRE 4 Comment fonctionne Ethereum

L’ère des applications blockchain ne fait que commencer. Ethereum doit devenir la plate-forme blockchain pour la construction d’applications décentralisées. Nous avons déjà appris dans les chapitres précédents que les cas publics d’utilisation de la blockchain ne se limitent pas aux crypto-monnaies, et que les possibilités ne sont limitées que par votre imagination !

Ethereum a déjà fait des percées dans de nombreux secteurs d’activité et fonctionne mieux non seulement pour les cas publics d’utilisation de la blockchain, mais aussi pour les cas privés. Ethereum a déjà établi une référence pour les plates-formes blockchain et doit être bien étudié pour être en mesure d’envisager comment les applications décentralisées utilisables peuvent être construites avec ou sans l’utilisation d’Ethereum. Aujourd’hui, il est possible de construire des applications blockchain avec une connaissance minimale de la cryptographie, la théorie des jeux, les mathématiques ou le codage complexe, et les fondamentaux de l’informatique, grâce à Ethereum.

Dans le chapitre 3, nous avons appris en détaillant précisément le protocole ainsi que l’application Bitcoin. Nous avons été témoins de la façon dont l’aspect crypto-monnaie est tellement imbriqué dans le protocole Bitcoin. Nous avons appris que Bitcoin n’est pas Bitcoin sur la blockchain, mais plutôt une blockchain Bitcoin. Dans ce chapitre, nous allons apprendre comment Ethereum a réussi à construire une couche de fondation abstraite qui est capable d’habiliter différents cas d’utilisation blockchain sur la même plate-forme blockchain.

La notion de « gas » sur Ethereum est une unité qui mesure la quantité d’effort de calcul qu’il faudra pour exécuter certaines opérations, à retenir pour la suite.

De Bitcoin à Ethereum

De toute évidence, la technologie blockchain est venu avec Bitcoin en 2009. Après que le Bitcoin ait résisté à l’épreuve du temps, les gens croyaient au potentiel de la blockchain. Les cas d’utilisation sont maintenant allés au-delà des secteurs bancaire et financier et ont enveloppé d’autres industries telles que la chaîne d’approvisionnement, le commerce de détail, le commerce électronique, les soins de santé, l’énergie et les secteurs gouvernementaux. C’est parce que différentes typologies de blockchain sont apparues et s’attaque à des problèmes d’affaires spécifiques. Néanmoins, il existe des plates-formes de blockchain publiques telles qu’Ethereum qui permettent de construire différents cas d’utilisation décentralisée sur la même plate-forme publique Ethereum.

Avec Bitcoins, la transaction décentralisée de crypto-monnaie entre pairs était possible. Les gens ont réalisé que la blockchain pouvait être utilisée pour effectuer des transactions et garder une trace de tout ce qui a de la valeur, pas seulement de la crypto-monnaie. Les gens ont commencé à explorer si le même réseau Bitcoin pouvait être utilisé pour tout autre cas d’utilisation.

Pour vous donner un exemple, “preuve d’existence” est l’un de ces cas d’utilisation où le hachage d’un document a été injecté dans le réseau blockchain Bitcoin afin que n’importe qui puisse plus tard vérifier qu’un tel document existait dans tel ou tel point dans le temps. Vitalik Butlerin a introduit la plate-forme blockchain Ethereum qui peut faciliter les transactions non seulement de l’argent, mais aussi des actions, des terres, du contenu numérique, des véhicules, et bien d’autres qui ont une certaine valeur intrinsèque. Jetons un œil à la figure 4-1.

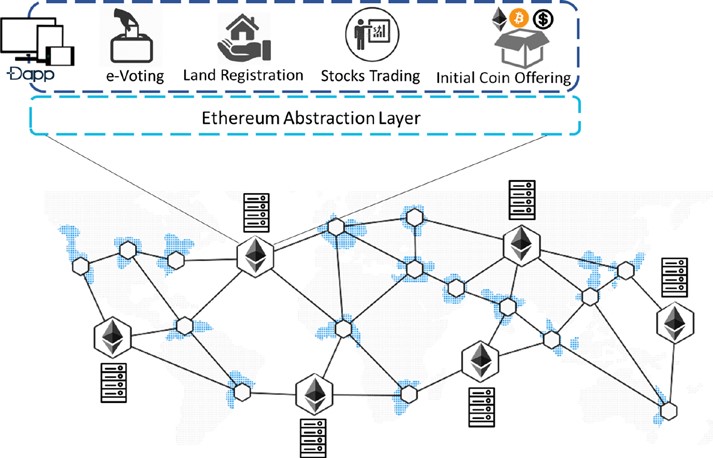
Figure 4-1. Multiples Applications décentralisées sur une plate-forme Ethereum

Comme Bitcoin, Ethereum est une plate-forme blockchain publique avec une philosophie de conception différente. L’approche la plus innovante a été de construire une couche d’abstraction de façon à ce que les transactions de différentes applications sont généralisées au code de programme qui peut s’exécuter sur tous les nœuds Ethereum. Même sur Ethereum, les mineurs génèrent l’Ether, une crypto-monnaie négociable à cause de laquelle le réseau public de blockchain est autosuffisant. Toute application qui est en cours d’exécution sur Ethereum doit payer des frais de transaction que finalement les mineurs obtiennent pour l’exécution des nœuds et le maintien de l’ensemble du réseau.

Ethereum comme blockchain nouvelle génération

Avec la blockchain Bitcoin, la communauté des développeurs a essayé de construire différentes applications décentralisées avec une blockchain complètement nouvelle, ou essayaient de modifier Bitcoin Core pour augmenter l’ensemble des fonctionnalités.

Quoi qu’il en soit, c’était compliqué. Un design différent avec un protocole alternatif était probablement une solution plus judicieuse, c’est pourquoi naquit la plate-forme blockchain Ethereum!

L’objectif était de faciliter le développement de nombreuses applications blockchain sur une plate-forme Ethereum plutôt que de construire des blockchains dédiées pour chaque application séparément. Ethereum a permis le développement rapide d’applications décentralisées qui pourraient interagir entre elles, assurant une sécurité adéquate.

Contrairement à Bitcoin, Ethereum a pris en charge le langage complet de Turing afin que n’importe qui puisse écrire des contrats intelligents qui pourraient pratiquement faire n’importe quoi sur une perspective de programmation. En outre, Ethereum est « stateful » par la conception et garde une trace des états de compte, qui est très différent de Bitcoin où tout reste comme une transaction et il n’y a pas de mémoire interne persistante pour les scripts. Avec l’aide d’une couche de fondation abstraite, les complexités sous-jacentes sont cachées aux développeurs et pas seulement cela ; les développeurs ont la flexibilité de concevoir leurs propres fonctions de transition d’état pour le transfert direct de valeur et d’information, et les formats de transaction.

Dans un effort pour atteindre l’objectif, l’innovation de base d’Ethereum a été la machine virtuelle Ethereum (EVM). La prise en charge des langues Turing-complètes via l’EVM permet aux développeurs de créer facilement des applications blockchain. Juste une machine virtuelle Java (JVM) est nécessaire pour exécuter le code Java, EVM est nécessaire pour exécuter les contrats intelligents. Pour l’instant, il suffit de garder à l’esprit que les contrats intelligents sont les scripts Ethereum écrits dans une langue Turing-complète qui est automatiquement exécuté au cas où un événement prédéfini se produit. Les “ScriptSig” et “ScriptPubKey” en Bitcoins sont les versions de base des contrats intelligents.

Nous avons appris dans le chapitre précédent que dans Bitcoins, l’ensemble des instructions était très limité. Dans Ethereum, cependant, on pourrait coder presque n’importe quel programme qui s’exécuterait sur l’EVM sur chaque nœud dans le réseau de blockchain Ethereum. Les applications décentralisées dans Ethereum sont appelées DApps. Ethereum étant un système informatique décentralisé mondial sans serveur centralisé, DApps sont les applications qui s’exécutent sans temps d’arrêt, fraude, ou toute sorte de réglementation. Un système de trésorerie électronique peer-to-peer tel que Bitcoin est très facile à construire sur Ethereum comme un DApps. De même, tout autre actif ayant une certaine valeur intrinsèque, comme la terre, les voitures, les maisons, les votes, etc., pourrait facilement être transigé par le biais de ses DApps respectifs sur Ethereum sous forme de jetons.

Contrairement au développement et au déploiement de logiciels traditionnels, DApps n’a pas besoin d’être hébergé sur un serveur back-end. Le « code » est intégré comme charge utile dans les transactions et sont ensuite envoyées aux nœuds de minage du réseau Ethereum.

De telles transactions seraient considérées par l’écosystème de minage en raison de l’ETH (Ether) comme le prix à payer. Comme dans Bitcoin, ces transactions sont diffusées à d’autres mineurs du réseau auxquels ils sont accessibles. La transaction finit par entrer dans un bloc et devient une partie éternelle de la blockchain lorsque le consensus est atteint. Les développeurs ont la liberté de coder n’importe quelle solution et de la déployer dans le réseau Ethereum. Le réseau exécute cela, tout seul, et valide et produit les sorties ainsi. Eh bien, si cela avait été sans aucun coût, le réseau n’aurait pas été durable. Il y a un prix associé à chaque transaction blockchain, et l’écriture d’un code et le déploiement dans le réseau Ethereum pourrait être une affaire coûteuse !

Philosophie de conception de l’Ethereum

Ethereum emprunte de nombreux concepts de Bitcoin Core comme il a résisté à l’épreuve du temps, mais est conçu avec une philosophie différente. Le développement d’Ethereum a été fait en suivant certains principes comme suit :

• Conception simpliste : La blockchain Ethereum est conçue pour être aussi simple que possible afin qu’elle soit facile à comprendre et à développer des applications décentralisées. Les complexités de la mise en œuvre sont maintenues à minima au niveau du consensus et sont gérés à un niveau supérieur à celui-ci. Par conséquent, la compilation linguistique de haut niveau ou la sérialisation/désérialisation des arguments, etc. ne sont pas une préoccupation pour les développeurs.
• Liberté de développement : La plate-forme Ethereum est conçue pour encourager toute forme de décentralisation sur sa plate-forme blockchain et ne discrimine ni ne favorise les cas d’utilisation spécifiques. Cette liberté est donnée dans la mesure où un développeur peut coder une boucle infinie dans un contrat intelligent et le déployer. Évidemment, la boucle fonctionnera aussi longtemps qu’ils paient les frais de transaction, et la boucle se termine finalement quand il est à court de « gaz ».
• Aucune notion de fonctionnalités : Dans un effort pour rendre le système plus généralisé, Ethereum n’a pas de fonctionnalités intégrées pour les développeurs à utiliser. Au lieu de cela, Ethereum fournit un support pour le langage Turing-complet et permet aux utilisateurs de développer leurs propres fonctionnalités comme ils le veulent. À partir de fonctionnalités de base telles que « l’heure de verrouillage » comme dans Bitcoin jusqu’aux cas d’utilisation à part entière, tout peut être codé dans Ethereum.

Entrez dans la Blockchain Ethereum

Nous avons appris l’objectif derrière Ethereum blockchain et sa philosophie de conception. Pour pouvoir comprendre et apprécier cette blockchain nouvelle- génération et construire des applications décentralisées sur elle, nous allons en apprendre davantage sur les composants de base de Ethereum en détail dans cette section.

Ethereum Blockchain

La structure de données ethereum blockchain est assez similaire à celle de Bitcoin, sauf qu’il y a beaucoup plus d’informations contenues dans l’en-tête de bloc pour le rendre plus robuste et aider à maintenir l’état correctement. Nous en apprendrons davantage sur les états Ethereum dans les sections suivantes. Concentrons-nous davantage sur la structure de données blockchain et l’en-tête dans cette section. Dans Bitcoins, il n’y avait qu’une seule racine de Merkle dans l’en-tête de bloc pour toutes les transactions dans un bloc. Dans Ethereum, il y a deux racines de plus de Merkle, il y a donc trois racines Merkle au total comme suit:

• stateRoot: Il aide à maintenir l’état global.
• transactionsRoot: Il s’agit de suivre et d’assurer l’intégrité de toutes les transactions dans un bloc, similaire à la racine Merkle de Bitcoin.
• receiptsRoot: C’est le hachage racine des reçus trie correspondant aux transactions dans un bloc

Nous allons observer ces racines Merkle dans leurs sections respectives de l’information en-tête d’un bloc. Pour mieux comprendre, jetez un coup d’œil à la figure 4-2.

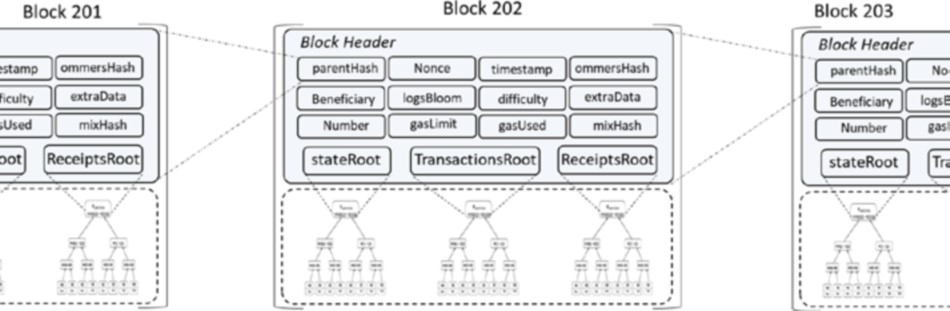
Figure 4-2. La structure de données blockchain d’Ethereum

Chaque bloc comprend généralement l’en-tête de bloc, la liste des transactions, la liste des oncles et les données supplémentaires facultatives. Jetons maintenant un coup d’œil aux champs d’en-tête pour comprendre ce qu’ils signifient et leur but d’être dans l’en-tête. Pendant que vous le faites, gardez à l’esprit qu’il pourrait y avoir de légères variantes de ces noms dans différents endroits, ou l’ordre dans lequel ils sont présentés pourrait être différent dans différents endroits. Nous vous suggérons de bien comprendre ces domaines afin que toute terminologie différente que vous pourriez rencontrer ne vous dérange pas beaucoup.

Section 1 : Bloquer les données Meta

• parentHash : Keccak 256 bits de hachage de l’en-tête du bloc parent, comme celui du style de Bitcoin
• timetamp : Le bloc de temps Unix courant
• number : Numéro de bloc du bloc actuel
• beneficiary : L’adresse 160 bits du compte « auteur » responsable de la création du bloc actuel auquel tous les droits provenant du minage réussie d’un bloc sont perçus

Section 2 : Références de données

• transactionsRoot : Le hachage racine Keccak 256 bits (racine de Merkle) des transactions trie peuplée de toutes les transactions dans ce bloc
• ommersHash : Il est autrement connu sous le nom “uncleHash.” C’est le hachage du segment des oncles du bloc, c’est-à-dire, Keccak 256 bits hachage de la partie de liste d’ommers de ce bloc (blocs qui sont connus pour avoir un parent égal au parent du parent du bloc actuel).
• extraData : tableau d’octet arbitraire contenant des données pertinentes à ce bloc. La taille de ces données est limitée à 32 octets (256 bits). Au moment d’écrire ces lignes, il est possible que ce champ devienne “extraDataHash”, ce qui indiquera les “extraData” contenues à l’intérieur du bloc. extraData pourrait être des données brutes, facturées à la même quantité de « gas ».

Section 3 : Informations d’exécution des transactions

• stateRoot : Le hachage racine Keccak 256 bits (racine de Merkle) de l’état final après validation et exécution de toutes les transactions de ce bloc
• receiptsRoot : Le hachage racine Keccak 256-bit (raceine de Merkle) du tri de reçus rempli avec les destinataires de chaque transaction dans ce bloc
• logBloom : Le filtre Bloom accumulé pour chacun des reçus des transactions Blooms, c’est-à-dire, le “OR” de toutes les Blooms pour les transactions dans le bloc
• gasUsed: La quantité totale de « gaz » utilisée par le biais de chacune des transactions de ce bloc
• gasLimit: La quantité maximale de « gaz » que ce bloc peut utiliser (valeur dynamique en fonction de l’activité dans le réseau)

Section 4 : Information sur le sous-système de consensus

• difficulty : La limite de difficulté pour ce bloc calculée à partir de la difficulté et de l’horodatage du bloc précédent
• mixHash : Le hachage de mélange de 256 bits combiné avec le ‘nonce’ pour le PoW de ce bloc
• nonce : Le nonce est un hachage de 64 bits qui est combiné avec mixHash et peut être utilisé comme une vérification PoW.

Comptes Ethereum

Les comptes Ethereum, contrairement aux Bitcoins, ne sont pas sous la forme de sorties de transactions non dépensées (UTXOs). Dans le chapitre Bitcoin, nous avons appris que les Bitcoins sont en fait présents sous la forme de transactions qui ont un propriétaire (la clé publique du propriétaire, adresse de 20 octets) et une valeur. Le propriétaire peut passer la transaction s’il a la clé privée valide pour la transaction qu’il essaie de dépenser. Bitcoin est donc un système de transition d’état où « état » se réfère à la collecte de tous les UTXOs. Chaque fois qu’un bloc est extrait, un changement d’état se produit parce que chaque bloc contient un tas de transactions où chaque transaction consomme UTXO (s) et produit UTXO(s).

L’état n’est pas encodé à l’intérieur des blocs. Ainsi, il n’y a aucune notion d’un solde de compte comme dans la conception de Bitcoin. Ethereum d’autre part est « stateful », et son unité de base est le compte. Chaque compte a un état associé à celui-ci et a également une adresse de 20 octets (160 bits) à travers laquelle il est identifié et référencé. Le but de la blockchain dans Ethereum est de garder une trace des changements d’état. Il existe généralement deux types de comptes Ethereum :

• Comptes détenus à l’extérieur (EOA) : Ces comptes sont également appelés « comptes simples » qui appartiennent généralement à des utilisateurs ou à des périphériques qui contrôlent ces comptes à l’aide de clés privées. Les EOA peuvent envoyer des transactions à d’autres EOA ou comptes contractuels en signant avec une clé privée. La transaction entre deux EOA est généralement de transférer toute forme de valeur. D’autre part, lorsqu’une EOA effectue une transaction vers un compte contractuel, le but est d’activer le « code » à l’intérieur du compte contractuel.
• Comptes contractuels : Ceux-ci ne sont contrôlés que par le code qu’ils contiennent. Ce code à l’intérieur des comptes contractuels est appelé « contrats intelligents ».

Ils sont généralement activés lorsqu’une transaction est envoyée au compte de contrat par les EOA ou par d’autres comptes contractuels. Même si les comptes contractuels sont capables d’exécuter des logiques métier complexes à travers le code qu’ils contiennent, ils ne peuvent pas initier de nouvelles transactions par eux-mêmes et dépendent toujours des EOA. Tout ce qu’ils peuvent faire est de répondre à d’autres transactions (évidemment en effectuant des transactions) selon la logique codée dans leur «code».

Jetez un coup d’œil aux trois scénarios suivants (figures 4-3 à 4-5) pour mieux comprendre la communication entre les EOA et les comptes contractuels.

Transaction EOA à EOA :

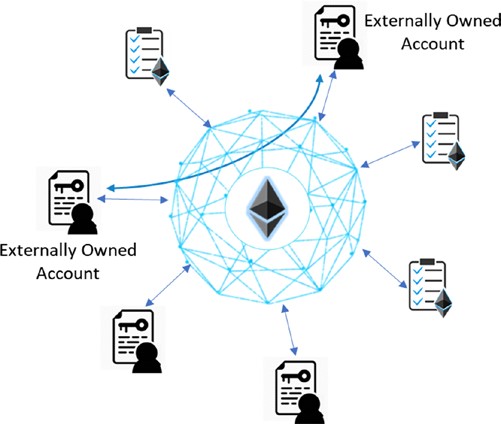
Figure 4-3. Transaction EOA à EOA

EOA à contrat transaction de compte :

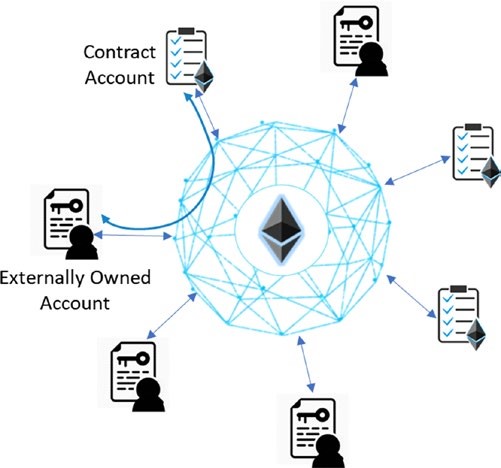
Figure 4-4. EOA à la transaction de compte de contrat

EOA à contrat de compte à d’autres transactions de compte de contrat :

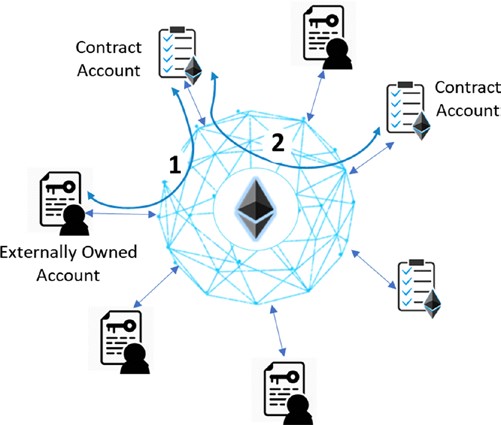
Figure 4-5. EOA à contrat de compte à la transaction de compte contractuel

Juste pour que les représentations précédentes ne soient pas déroutantes, sachez que les comptes contractuels sont internes et que les communications entre elles le sont également. Contrairement aux comptes EOA où les EOA font une transaction qui est injectée dans la blockchain, les comptes contractuels et les transactions entre eux sont des phénomènes internes.

Avantages des UTXOs

La perspective de conception de Bitcoin était de maintenir l’anonymat dans une mesure possible. Lorsque nous le comparons à Ethereum, les avantages suivants de l’UTXOs sont beaucoup plus importantes :

• Meilleure confidentialité : Dans Bitcoins, il est conseillé d’utiliser une nouvelle adresse lors de la réception des transactions, ce qui contribue à renforcer l’anonymat. Même avec des techniques statistiques ou d’apprentissage automatique sophistiquées, il est difficile de relier les comptes ensemble, mais pas impossible.
• Potentiellement plus évolutif : La discussion relative à l’évolutivité est généralement très subjective et dépend du contexte, du cas d’utilisation à portée de main et de nombreux autres facteurs. L’intention ici est de mentionner simplement le potentiel inhérent d’UTXO à l’échelle. Il est très facile d’exécuter les transactions en parallèle. En outre, lorsqu’un propriétaire ou d’autres nœuds conservant les données de preuve de propriété Merkle pour certaines pièces perdent ces données, seul le propriétaire est touché. Au contraire, lorsque les données d’arbre Merkle pour certains comptes sont perdues, alors toute opération sur ce compte ne serait pas faisable, même l’envoi.

Avantages des comptes

Même si Ethereum en tout cas est une extension de Bitcoin, il est imaginé avec un tout nouveau design avec son propre ensemble compromis d’avantages-inconvénients. Jetons un coup d’oeil aux avantages suivants des comptes Ethereum par rapport à la conception Bitcoin:

• Économie d’espace significative : Dans Bitcoin, lorsque plusieurs transactions sont regroupées pour effectuer une transaction (par exemple, si vous devez effectuer une transaction de 5BTC et que vous n’avez jamais reçu une transaction avec au moins 5BTC que vous pourriez utiliser, vous devez regrouper plusieurs transactions afin le total dépasse 5BTC), de nombreuses références à ces transactions individuelles doivent être faites. Aussi, toutes ces transactions doivent avoir des adresses différentes, donc autant de transactions, autant d’adresses aussi! Dans les comptes Ethereum, cependant, une seule référence à un compte est suffisante. Même si Ethereum utilise l’arbre de Patricia Merkle (MPT), qui est un peu plus gourmand en espace que l’arbre Merkle, vous finissez par économiser une quantité importante d’espace pour les transactions complexes.
• Simple à coder : Avec les UTXO et les scripts qui ne sont pas Turing-complets, il est difficile de concevoir des systèmes complexes. Les UTXO peuvent être dépensés ou non dépensés; il n’y a pas d’autre état possible entre les deux. Ce qui rend difficile le code des logiques commerciales complexes. Même si les scripts sont habilités à faire plus, il devient plus compliqué par rapport à l’utilisation de comptes. Étant donné que l’objectif d’Ethereum est d’aller au-delà de la crypto-monnaie et d’accueillir différents types de cas d’utilisation (par le biais de DApps), un système basé sur les comptes est presque inévitable.
• Référence client légère : Contrairement aux clients Bitcoin, les applications clientes Ethereum peuvent accéder facilement et rapidement à toutes les données liées à un compte en scannant l’arbre d’état dans une direction spécifique. Dans le modèle UTXO, il existe généralement plusieurs références à plusieurs transactions associées à une transaction spécifique à l’étude.

État du compte

Nous avons appris que chaque compte a un état associé à celui-ci. Nous avons également examiné les deux types de comptes qui existent avec Ethereum, l’un est un compte contractuel et l’autre est un compte externe ou EOA. Quel que soit le type de compte, ils sont suivis par la racine Merkle “stateRoot” dans l’en-tête de bloc et peuvent apparaître comme indiqué dans la figure 4-6.

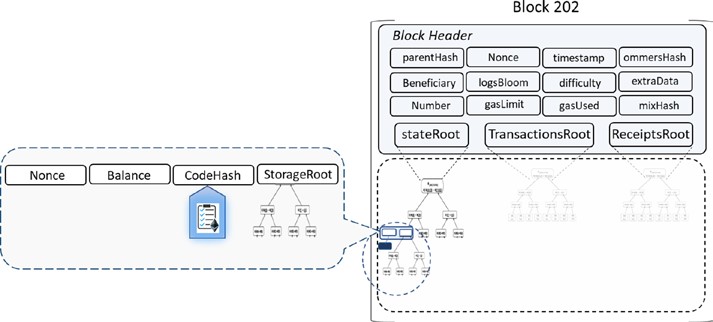
Figure 4-6. Zoom sur la représentation de l’état de compte

Comme vous pouvez le voir dans le chiffre, indépendamment du fait que le compte est un EOA ou un compte de contrat, il a les quatre composantes suivantes:

• Balance : Solde total “Ether” dans le compte. Plus précisément, le nombre de Wei appartenant à l’adresse(1ETH 10¹⁸ Wei)
• CodeHash: C’est le hachage du « code ». Chaque compte de contrat possède un “code” qui est exécuté sur l’EVM. Le hachage de ce code est stocké dans ce champ CodeHash. Pour les comptes EOA, cependant, il n’y a pas de «code», de sorte que le champ CodeHash contient le hachage de la chaîne vide.
• StorageRoot: C’est le hachage racine de 256 bits de l’arbre Merkle qui code le contenu de stockage d’un compte. Le MPT code le hachage du contenu de stockage. Garder le hachage de racine de cet arbre dans le champ de racine de stockage aide à suivre le contenu d’un compte et aide également à assurer son intégrité.
• Nonce: Il s’agit d’un compteur qui garantit que chaque transaction n’est traitée qu’une seule fois. Pour les EOA, ce nombre représente le nombre de transactions à partir de l’adresse du compte. Pour les comptes contractuels, il représente le nombre de contrats créés par ce compte.

Ainsi, ce sont les essais «d’état» qui sont chargés de suivre les changements d’état de la blockchain Ethereum. Cependant, ce qui est un peu délicat, c’est que l’état n’est pas directement stocké dans chaque bloc, plutôt sous la forme de données d’état encodées par RLP (Recursive Length Prefix) dans MPT à chaque nœud Ethereum. Ainsi, pour maintenir l’état global, la chaîne de blocs Ethereum comprend des «racines d’état» dans chaque bloc qui stocke le hachage racine de l’arbre de hachage (racine Merkle) représentant l’état du système au moment de la création du bloc.

Selon le Livre Jaune Ethereum, l'”Etat mondial” est une cartographie entre les adresses (identificateurs 160 bits) et les états de compte. Ainsi, l’État mondial a l’information de tous les comptes dans la blockchain, mais n’est pas stocké dans chaque bloc. Chaque bloc ne modifie que certaines parties de l’état. D’une certaine manière, l’État mondial est généré en traitant chaque bloc depuis le bloc de genèse. Certains nœuds Ethereum peuvent choisir de maintenir tous les états historiques en conservant toutes les transactions historiques, c’est-à-dire les transitions d’État et leurs sorties. Cela permet aux clients de s’interroger sur l’état de la blockchain à tout moment, même pour les historiques, sans avoir à tout recalculer dès le début. La récupération des informations d’état est similaire à une requête globale dans SQL où les données sont facilement disponibles; seulement une agrégation est nécessaire. Ainsi, les anciennes données d’état peuvent facilement être jetées (ceci est connu sous le nom de « taille ») parce qu’elles peuvent être calculées en arrière en cas de besoin. Eh bien, les données de l’État par la conception est implicite dada, ce qui signifie que l’information de l’État doit être calculé.

Utilisation de Trie

Nous avons appris les trois types d’essais qui ont leurs racines dans l’en-tête de bloc. Ces racines sont essentiellement les pointeurs de ces trois trie. Bien que nous ayons examiné les explications d’une seule ligne de ces trie dans les sections précédentes, nous allons simplement les revoir avec un choix légèrement différent de mots

• L’État Trie: Il représente l’état entier (l’État global) après avoir accédé au bloc.
• Le Trie de transaction : il représente toutes les transactions dans un bloc index (c.-à-d. key:0 pour la première transaction à exécuter, clé:1 pour la deuxième transaction, etc.). Remémorez-vous des principes fondamentaux du MPT que nous avons abordés plus tôt et que nous essayons de corréler.
• Le Trie de réception : Il représente les « reçus » correspondant à chaque transaction. Un reçu pour une transaction est une structure de données codée RLP comme indiqué ci-après :

[ medstate, gas_used, logbloom, logs ]

Nous allons maintenant creuser plus profondément dans le trie Reçu que nous n’avons pas encore couvert les bases de ce sujet. Jetez un oeil à tous les champs dans le Trie De réception

Structure de données codées par RLP et suivi des descriptions suivantes pour ces champs :

• medstate : C’est la racine de trie d’état après le traitement de la transaction. Une transaction réussie met à jour l’état Ethereum.
• gas_used : C’est la quantité totale de gaz utilisée pour le traitement de la transaction.
• logs : Il s’agit d’une liste d’éléments du formulaire- [adresse, [sujet1, sujet2…], données]
• Ces éléments de liste sont produits par le LOG0, LOG1… opcodes pendant l’exécution de la transaction. Le champ « adresse » est l’adresse du contrat qui a produit le journal, les champs « sujets » sont jusqu’à quatre valeurs de 32 octets, et le champ « données » est un tableau d’octets de taille arbitraire.
• Logbloom: Il s’agit d’un filtre Bloom composé des adresses et des sujets de tous les journaux de la transaction. C’est différent de celui présent dans l’en-tête de bloc.

L’arbre de Patricia (MPT : Merkle Patricia Tree)

Dans Ethereum, les comptes sont cartographiés avec leurs états respectifs.

La cartographie entre tous les comptes Ethereum, y compris les EOA et les comptes contractuels avec leurs États, est collectivement appelée États du monde. Pour stocker ces données cartographiques, la structure de données utilisée dans Ethereum est le MPT. Ainsi, MPT est la principale structure de données utilisée dans Ethereum qui est autrement connu sous le nom Merkle Patricia trie. Nous avons appris sur les arbres Merkle dans le chapitre Bitcoin, qui nous emmène déjà à mi-chemin dans la compréhension MPT. MPT est en fait dérivé en prenant des éléments à la fois de l’arbre de merkle et de l’arbre de Patricia.

Se rappeler du chapitre Bitcoin que les arbres Merkle sont les hachages binaires où les nœuds de feuilles contiennent le hachage des blocs de données et chaque nœud non feuille contient les hachages de leurs noeuds enfant. Lorsqu’une telle structure de données est implémentée, il devient facile de vérifier si une certaine transaction faisait partie d’un bloc. Ce n’est qu’en utilisant très peu d’informations de l’ensemble du bloc, c’est-à-dire en utilisant seulement la branche Merkle au lieu de l’arbre entier, fournir une preuve d’appartenance a été assez facile. Les arbres de Merkle facilitent une vérification efficace et sécurisée du contenu dans les systèmes décentralisés. Au lieu de télécharger chaque transaction et chaque bloc, les clients légers ne peuvent télécharger la chaîne d’en-têtes de bloc, c’est-à-dire, des morceaux de 80- octets de données pour chaque bloc qui contiennent seulement cinq choses: le hachage de l’en-tête du bloc précédent, l’horodatage, la difficulté de minage, la valeur nonce qui satisfait PoW, et le hachage racine de l’arbre Merkle contenant toutes les transactions pour ce bloc. Bien qu’il soit très utile et intéressant, à l’exeption de valider la preuve d’adhésion pour une transaction dans un bloc, il n’y a rien que vous pourriez faire. Une limitation particulière est qu’aucune information ne peut être prouvée sur l’état actuel (par exemple, le total des avoirs numériques, les enregistrements de noms, l’état des contrats financiers). Même pour vérifier combien de Bitcoins vous détenez, beaucoup d’interrogations et de validation sont impliquées.

Les arbres Patricia, quant à eux, sont une forme d’arbres Radix. Le nom PATRICIA (Practical Algorithm to Retrieve Information Coded In Alphanumeric) signifie « Algorithme pratique pour récupérer l’information codée en alphanumérique ». Un arbre Patricia facilite les opérations efficaces d’insertion/suppression. Les recherches de valeur clé dans l’arbre Patricia sont très efficaces. Les clés sont toujours codées dans le chemin. Ainsi, “key” est le chemin que vous prenez de la racine jusqu’au nœud de feuille où la “valeur” est stockée. Les touches sont généralement les cordes qui aident à descendre le chemin où chaque personnage indique quel nœud enfant suivre pour atteindre le nœud de la feuille et trouver ainsi la valeur stockée dedans.

Ainsi, les MPT fournissent une structure de données authentifiée cryptographiquement utilisée pour stocker toutes les liaisons (clés, valeur) dans Ethereum. Ils sont entièrement déterministes, ce qui signifie qu’un arbre Patricia avec les mêmes liaisons (clé, valeur) sera sûrement le même jusqu’au dernier octet. Les opérations d’insertion, de recherche et de suppression sont très efficaces avec la complexité o(log(n)). En raison de la partie Merkle dans MPT, le hachage d’un nœud est utilisé comme pointeur du nœud et le MPT est construit en conséquence, où Key == SHA3(RLP(value)).

Bien que la partie Merkle offre une structure d’arbre inviolable et déterministe, la partie Patricia fournit une fonction efficace de récupération d’information. Ainsi, si vous remarquez, le nœud racine dans MPT devient une empreinte cryptographique de toute la structure de données. Dans le réseau Ethereum P2P, lorsque les transactions sont diffusées, elles sont assemblées par tous les nœuds miniers qui les ont reçues. Les nœuds forment alors un arbre (alias trie) et calculent le hachage de racine pour inclure dans l’en-tête de bloc. Bien que les transactions soient stockées localement dans l’arbre, elles sont envoyées à d’autres nœuds ou clients après avoir été sérialisées sur des listes. Les parties réceptrices doivent les désérialiser pour former l’arbre de transaction pour vérifier à l’aide du hachage racine. Dans Ethereum, les MPT sont un peu modifiés pour un meilleur ajustement avec la mise en œuvre Ethereum. Au lieu de binaire, l’hexadecimal est utilisé. Par conséquent, les nœuds dans l’arbre ou le trie ont 16 nœuds enfant (l’alphabet hex de 16 caractères) et une profondeur maximale de X. un caractère hex est appelé un “nibble” dans de nombreux endroits.

L’idée de base d’un MPT dans Ethereum est que pour une seule opération, il ne modifiera que la quantité minimale de nœuds pour recalculer le hachage racine. De cette façon, le stockage et les complexités sont maintenus minimes.

Encodage RLP

Vous devez avoir remarqué que nous avons mentionné l’encodage RLP dans les sections précédentes. RLP signifie Récursif Longueur Préfixe. Il s’agit d’une méthode de sérialisation utilisée dans Ethereum pour les blocs, les transactions et les messages de protocole tout en envoyant des données sur le fil et aussi pour les données d’état de compte tout en sauvant l’état dans l’arbre Patricia. En général, lorsque des structures de données complexes doivent être stockées ou transmises, puis reconstruites à l’extrémité de réception pour le traitement, la sérialisation d’objets est une bonne pratique.

RLP en ce sens est similaire à JSON et XML, mais RLP est considéré comme plus minimaliste, l’espace efficace, simple à mettre en œuvre, et garantit une cohérence absolue octet-parfait. C’est pourquoi RLP a été choisi pour être la principale technique de sérialisation pour Ethereum. Son seul but est de stocker des rangées d’octets. Il n’essaie pas non plus de définir des types de données spécifiques, tels que Booleans, floats, doubles, integers, etc., et n’est conçu que pour stocker la structure sous forme de tableaux imbriqués. Les cartes clés/valeur ne sont pas explicitement prises en charge par RLP. Ainsi, il est conseillé de représenter des cartes telles que [k1, v1], [k2, v2], …], où k1, k2… sont dans l’ordre lexicographique (triés à l’aide de la commande standard pour les strings). Alternativement, utilisez l’encodage de l’arbre Patricia de niveau supérieur qui a un schéma de codage RLP inhérent.

Veuillez garder à l’esprit que RLP est utilisé uniquement pour coder la structure des données et n’est absolument pas au courant du type d’objet codé. Bien qu’il aide à réduire la taille du tableau d’encodage des octets bruts, l’extrémité de décodage doit être conscient du type d’objet qu’il essaie de décoder.

Ethereum Transaction et structure de message

Dans la section précédente, nous avons examiné la structure du bloc et les différents champs dans l’en-tête du bloc. Pour qu’une transaction soit qualifiée par les mineurs ou les nœuds Ethereum, elle doit avoir une structure normalisée. Une transaction Ethereum typique (par exemple, ce que vous passez par sendRawTransaction() que nous verrons plus tard) se compose des champs suivants:

• nonce: Il s’agit d’un entier, juste un compteur égal au nombre de transactions envoyées par le compte expéditeur, c’est-à-dire, numéro de séquence de transaction.
• gasPrice : Prix que vous êtes prêt à payer en termes de nombre de Wei à payer par unité de gas
• gasLimit : La quantité maximale de gas qui doit être utilisée dans l’exécution de cette transaction, ce qui limite également le nombre maximal d’étapes de calcul que l’exécution de la transaction est autorisée à prendre
• To : L’adresse de 160 bits du bénéficiaire ou l’adresse du contrat. Pour la transaction qui est utilisée pour créer un contrat (cela signifie que l’adresse du contrat n’existe pas encore), elle est gardée vide.
• Value : Ether total (nombre de Wei) à transférer au destinataire par l’expéditeur de la transaction
• V, r, s : valeurs correspondant à la signature ECDSA de la transaction; représentent également l’expéditeur de cette transaction
• init : Ce n’est pas vraiment un champ facultatif, seulement utilisé avec les transactions utilisées pour la création de contrats. Ce champ peut contenir un tableau d’octet de taille illimitée spécifiant le code EVM pour la procédure d’initialisation du compte.
• L’opcode “init” n’est utilisé qu’une seule fois pour l’initialisation du nouveau compte de contrat et est jeté par la suite. Il retourne le corps du code de compte après l’avoir associé au compte contractuel. Cette association est un phénomène permanent et ne change jamais.
• Data : Champ optionnel qui peut contenir un message à envoyer à un contrat ou à un simple compte. Il n’a pas de fonction spéciale en tant que telle par défaut, mais l’EVM a un opcode — à l’aide duquel, un contrat peut accéder à ce champ de données et effectuer les calculs nécessaires et les placer dans le stockage.

Notez soigneusement que les champs susmentionnés sont fournis dans l’ordre spécifié et sont tous codés par RLP, à l’exception des noms de champ. Ainsi, une transaction Ethereum signifie en fait un paquet de données signé avec ces champs. Les champs gasPrice et gasLimit sont importants pour prévenir les attaques par déni de service. Afin d’éviter les tentatives accidentelles ou délibérées de boucles infinies ou d’autres gaspillages informatiques dans le code, chaque transaction est nécessaire pour définir une limite sur le nombre d’étapes de calcul pour l’exécution du code qu’elle peut utiliser.

Les transactions Ethereum sont en fait les « fonctions de transition de l’état » parce qu’une transaction réussie change l’état. En outre, le résultat de ces transactions peut être stocké, comme nous l’avons déjà examiné dans la section “État du compte” précédemment.

Les messages Ethereum, quant à eux, sont comme des transactions, mais ne sont déclenchés que par des comptes de contrat et non par des EOA. En outre, les messages sont uniquement destinés à être entre les comptes du contrat, en raison desquels ils sont également appelés «transactions internes». Ainsi, les contrats ont la capacité d’envoyer des messages à d’autres contrats.

En règle générale, un message est produit lorsqu’un contrat, lors de l’exécution de son code, rencontre les opcodes « CALL » ou « DELEGATECALL ». Ainsi, les messages sont plus comme des appels de fonction qui existent dans l’environnement d’exécution Ethereum. Il est également important de noter que les messages sont toujours brut et jamais sérialisés ou en série. Un message contient les champs suivants :

• Sender : L’expéditeur du message comme une option implicite
• Recipient : L’adresse du contrat bénéficiaire à qui on fait l’envoi
• Value : Le montant de Wei à transférer à l’adresse du contrat avec le message
• Data : Champ facultatif, mais peut contenir des données d’entrée pour le contrat de destinataire fournies par l’expéditeur
• gasLimit : Valeur qui limite la quantité maximale de gas que l’exécution du code peut consommer lorsqu’elle est déclenchée par le message. Il est également appelé “startGas“.

Nous avons examiné la transaction et les messages. Une transaction Ethereum peut aller d’une EOA à une EOA, ou d’une EOA à un compte contractuel. Il existe une autre situation où une transaction à partir d’une EOA est lancée pour créer un compte de contrat (se souvenir du champ “init” que nous venons de couvrir).

Maintenant, il suffit de penser à ce qu’est exactement une transaction? C’est certainement le pont entre le monde extérieur et la blockchain Ethereum, mais quoi de plus? Si vous effectuez un zoom avant vers une transaction, vous verrez qu’il s’agit d’une instruction, initiée par l’EOA en la signant, qui est sérialisée et soumise à la blockchain. Jetez un coup d’œil à la figure 4-7.

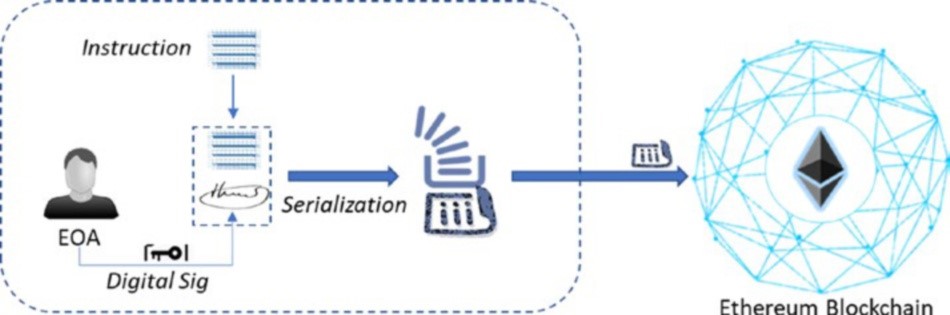
Figure 4-7. Initiation de la transaction

Maintenant, que se passe-t-il après l’injection d’une transaction dans la blockchain ? Eh bien, il commence à exécuter à chaque nœud Ethereum si elle est jugée valide. Pendant que cette transaction est en cours d’exécution, Ethereum est conçu pour garder un œil sur le « substate » pour suivre le flux d’exécution. C’est parce que, si une transaction n’est pas terminée en raison de « running out of gas », alors l’exécution entière jusqu’à présent doit être retournée. De plus, les informations recueillies lors de l’exécution sont requises immédiatement après l’achèvement de la transaction. Ainsi, le « substate » contient ce qui suit:

• Self-destruct set: un ensemble de comptes (le cas échéant) qui seront jetés après l’achèvement de la transaction
• Log series: « Chackpoints » archivés et indexables de l’exécution du code de l’EVM pour suivre les appels contractuels
• Refund balance : Il s’agit du montant à rembourser au compte expéditeur après l’exécution des transactions.Le stockage dans Ethereum est assez cher, il y a donc une instruction SSTORE dans Ethereum qui est utilisé comme un compteur de remboursement. Le compteur de remboursement commence à zéro (pas d’état de remboursement) et est incrémenté chaque fois que la transaction ou le contrat supprime quelque chose du stockage. Ce montant de remboursement est différent et en plus du gas inutilisé qui est remboursé à l’expéditeur.

Dans les versions antérieures d’Ethereum, qu’il s’agisse d’une transaction ou d’un contrat qui s’exécute avec succès ou échoue entre les deux, le gas entier utilisé est consommé. Ce n’était pas toujours logique. Si une exécution s’arrêtait en raison d’un problème d’autorisation ou de permission ou de tout autre problème, l’exécution cesserait et le gas restant serait toujours consommé. La dernière mise à jour Byzantium a introduit le code “revert” comme une manipulation d’exception. Dans le cas où un contrat doit s’arrêter, “revert” pourrait être utilisé pour inverser les changements d’état, retourner à la raison de l’échec, et créditer le gas restant à l’expéditeur. Après l’exécution réussie des transactions ou des contrats, une transition d’état se produit.

Nous avons regardé blockchaininfo pour voir une transaction Bitcoin en direct, si vous jetez un oeil à https://etherscan.io pour Ethereum, vous trouverez les informations suivantes:

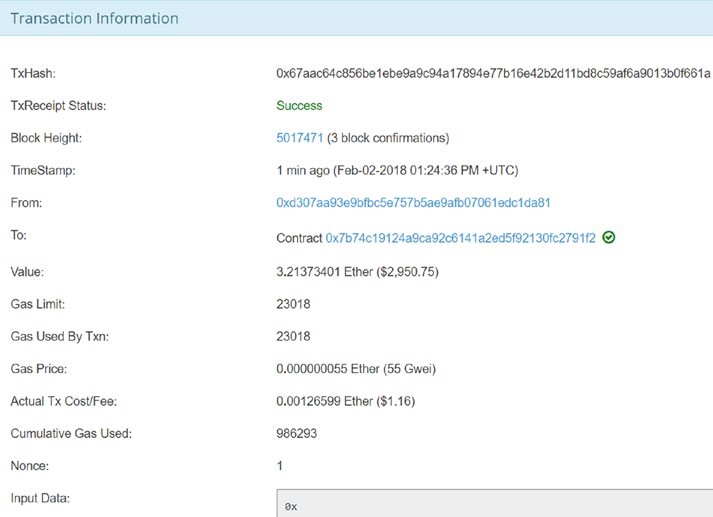
Fonction de transaction d’état Ethereum

Dans la section précédente, nous avons entendu parler des transactions et des messages ethereum. Nous sommes maintenant conscients qu’une transition d’état se produit chaque fois qu’une transaction est passée, avec succès. Ainsi, la fonction de transition d’état dans Ethereum est :

APPLY (S,Tx) -> S’ \\ où S est l’ancien état et S’ est le nouvel état

Jetez un coup d’œil à la figure 4-8.

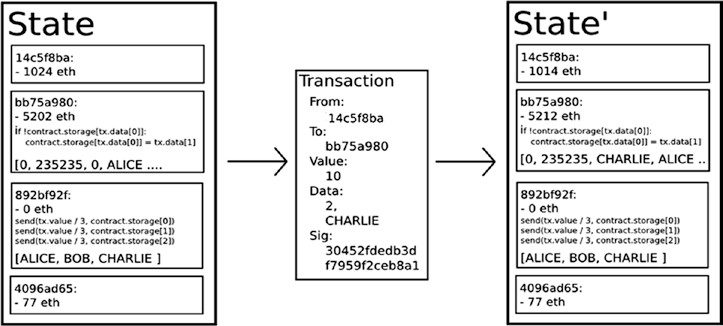
Figure 4-8. Fonction de transition de l’état Ethereum

Ainsi, la fonction de transition d’état lorsque Tx est appliqué à l’état S pour entraîner un état S’ modifié peut être définie comme suit :

• Valide la transaction pour voir si elle est bien formée.
• A le bon nombre de valeurs
• La signature est valide.
• Le nonce correspond au nonce dans le compte de l’expéditeur.

Si l’un des points précédents n’est pas valide, une erreur est retournée.

• Calcule les frais et réglez les comptes.
• Calcule les frais de transaction en tant que gasLimit * gasPrice.
• Détermine l’adresse d’envoi à partir de la signature.
• Soustrait les frais du solde du compte de l’expéditeur et l’augmentation du nonce de l’expéditeur.

S’il n’y a pas assez d’équilibre à dépenser, retournez une erreur.

• Initialize GAS – gasLimit, et enlever une certaine quantité de gaz par octet pour payer les octets comme frais de transaction.
• Transfére la valeur de la transaction (peut être n’importe quelle valeur) du compte de l’expéditeur vers le compte de réception. La transaction pourrait être pour quelque chose comme un terrain, un véhicule, un jetons ERC20, etc, mais le prix du gas doit être en Ether afin que les mineurs acceptent la transaction. Si le compte de réception n’existe pas encore, créez-le.
• Si le compte de réception est un contrat et non une EOA, puis exécutez le code du contrat soit à l’achèvement ou jusqu’à ce que l’exécution est à court de gaz. Le code de contrat est exécuté sur l’EVM de chaque nœud dans le cadre du processus de validation de bloc afin que le bloc, donc la post-exécution de sortie du contrat, fasse partie de la chaîne de blocs principale.
• Si le transfert de valeur a échoué parce que l’expéditeur n’avait pas assez d’argent, ou l’exécution du code est à court de gaz, tous les changements d’état sont inversés (grâce à la mise en œuvre MPT) sauf le paiement des frais, et ajout des frais au compte du mineur.
• Dans le cas contraire, rembourse les frais pour tout le gaz restant à l’expéditeur, et envoye les frais payés déjà pour le gaz consommé au mineur.

Coût du gaz et des transactions

Les transactions sur Ethereum fonctionnent sur le «gas», l’unité fondamentale de calcul à Ethereum. Chaque transaction, qu’elle s’agisse d’une EOA ou d’un contrat, doit avoir le gasLimit et gasPrice pour calculer les frais. Ces frais sont versés aux mineurs pour les indemniser de leurs contributions aux ressources et du travail qu’ils effectuent. Évidemment, les mineurs ont le choix d’inclure la transaction et de percevoir les frais, similaire à celui de Bitcoin.

Habituellement, une étape de calcul ne coûte qu’un seul gas,mais une partie des opérations de calcul ou destockage à forte intensité coûte ntre plus cher. Pour chaque octet de données de transaction, environ cinq gas sont nécessaires. Jetez un oeil à ces exemples d’exemples:

• l’ajout de deux numéros (avec EVM opcode ADD) nécessite environ trois gas;
• multiplier deux nombres (avec EVM opcode MUL) nécessite environ cinq gas;
• le calcul d’un hachage (SHA3) nécessite environ 30 gaz (calcul intensif, vous voyez).

Le coût de stockage est également calculé de la même manière, mais assez cher pour de bonnes raisons. Selon la conception, une transaction peut inclure une quantité illimitée de données. Il en coûte 68 gas par octet de données de transaction non nulles. Pour stocker un mot 256 bits dans un « contrat », environ 20 000 gas sont nécessaires. Vous pourriez trouver plus d’opcodes et leurs prix correspondants dans le papier jaune Ethereum. Le coût serait alors simplement multiplier le gas nécessaire avec le gasPrice.

Contrairement à Bitcoin, le calcul des coûts Ethereum est plus complexe. Il prend en compte les coûts de bande passante, de stockage et de calcul. Avoir un tel mécanisme de calcul des frais empêche le réseau Ethereum d’un attaquant qui pourrait simplement vouloir injecter une boucle infinie pour le calcul (conduisant à des attaques de déni de service) ou consommer de plus en plus d’espace en stockant des données vides de sens.

Le coût total d’une transaction dépend en fait de la quantité de gaz consommée par la transaction, multipliée par le prix d’une unité de gas spécifiée dans la transaction par l’initiateur de la transaction. Les mineurs, quant à eux, ont une stratégie de calcul du prix du gas à facturer, qui devrait être au moins la quantité que l’expéditeur d’une transaction doit spécifier afin que la transaction ne soit pas rejetée par le mineur. Alors, comment calculez-vous le coût total d’une transaction? Pas approximatif, mais le coût réel?

Le coût total “Ether” d’une transaction est basé sur deux facteurs: gasUsed et gasPrice. Coût total = gasUsed * gasPrice. Le composant gasused est le gasz total consommé lors de l’expiration des opcodes EVM pour les instructions, et gasPrice est celui spécifié par l’utilisateur.

Si la quantité totale de gaz utilisée par les étapes de calcul (y compris la transaction, le message et tout sous-message qui peut être déclenché) est inférieure ou égale à la limite de gaz, alors la transaction est traitée par le mineur.

Toutefois, si le gaz total dépasse la limite de gaz,alors tous les changements sont retournés (bien qu’il s’agit d’une transaction valide), sauf que les frais peuvent encore être perçus par le mineur. Alors, qu’advient-il de l’excès de gas? Tout le gas inutilisé après l’exécution de la transaction est remboursé à l’expéditeur sous le nom d’Éther. Les expéditeurs n’ont pas besoin de s’inquiéter des dépenses excessives, car ils ne sont facturés que pour le gas consommé. Cela signifie qu’il est important ainsi que sécurisé d’envoyer des transactions avec une limite de gas bien au-dessus des estimations. Il est également recommandé de ne pas payer le prix très élevé de et d’utiliser le prix moyen du gas depuis https://ethgasstation.info/.

Passons en revue chaque étape lorsqu’une transaction est effectuée dans un réseau Ethereum pour construire une compréhension concrète du flux :

• Chaque transaction doit définir un “gasLimit” qu’il est prêt à dépenser (gasLimit est également appelé “startGas“), et les frais qu’il est prêt à payer par unité de gas (gasPrice). Au début de l’exécution, la valeur Ether du gasLimit * gasPrice est retiré du compte de l’expéditeur de la transaction. Rappelez-vous que ce n’est pas vraiment le coût total d’une transaction (devrait être un peu plus que cela dans un cas idéal). Ce n’est qu’après la transaction, son coût réel est conclu (gazUsed * gasPrice) qui est ajusté de ce (gazLimit * gasPrice), qui a été initialement déduit du compte de l’expéditeur et le montant du solde est crédité à l’expéditeur. Au début d’une transaction elle-même, le montant (gazLimit * gasPrice) est déduit parce qu’il pourrait y avoir une possibilité que l’expéditeur pourrait être insovable pendant que la transaction qu’ils ont initiée est à mi-parcours.
• Toutes les opérations pendant l’exécution des transactions, y compris les lectures et les écritures de base de données, les messages et toutes les mesures de calcul prises par le EVM tels que l’addition, la soustraction, le hachage, etc. consomment une certaine quantité de gaz qui est prédéfinie.
• Une transaction normale est une transaction qui s’exécute avec succès sans dépasser le gasLimit spécifié. Pour de telles transactions, il devrait rester du gas, disons, «gas_rem». Après une exécution réussie de transaction, l’expéditeur de la transaction reçoit un remboursement de «gas_rem * gasPrice» et le mineur du bloc reçoit une récompense de « (gasLimit – gas_rem) * gasPrice ».
• Si une transaction est à court de gas avant d’être complétée, toutes les exécutions retournent, mais la transaction est néanmoins valide. Dans de telles situations, le seul résultat de la transaction est que le montant total “gazLimit * gasPrice” est alloué au mineur.
• Dans le cas des comptes contractuels, lorsqu’un contrat envoie un message à l’autre contrat de sous-exécution, il a également la possibilité de définir une limite de gas. Cette option est spécifiquement destinée à la sous-exécution découlant de ce message, car il est possible que le contrat appelé ait une boucle infinie. Si la sous-exécution est à court de gas,alors la sous-exécution est retournée, ce qui protège contre de telles boucles infinies ou des tentatives délibérées d’attaques DoS. Le gas est consommé de toute façon et attribué au mineur. Notez également que lorsqu’un message est déclenché par un contrat, seules les instructions coûtent du gas,mais les données d’un message ne coûtent pas de gas. C’est parce que les données du contrat parent n’ont pas besoin d’être copiées à nouveau, et pourrait être simplement référencé par un pointeur.

La première Release Ethereum (Frontiere) avait un prix de gaz par défaut de 0,05e12 WEI (c.-à-d., la plus petite dénomination d’Ether). Dans le deuxième Release Ethereum (Homestead), le prix du gas par défaut a été réduit à 0,02e12 WEI. Vous devez vous demander pourquoi le gas et l’éther sont découplés l’un de l’autre et pas une seule unité de mesure, ce qui l’aurait rendu beaucoup plus simple. Eh bien, il est délibérément conçu de cette façon parce que les unités de gas bien aligner avec les unités de calcul ayant un coût naturel (par exemple, le coût par calcul), tandis que le prix de l’éther fluctue généralement en raison des fluctuations du marché.

Nous savons déjà que chaque nœud Ethereum participant au réseau exécute l’EVM dans le cadre du protocole de vérification par blocs. Cela signifie que tous les nœuds exécutent le même ensemble de transactions et de contrats (redondant parallèle, mais essentiel pour le consensus). Bien que cette redondation le rend naturellement cher, il y a une incitation à ne pas utiliser la blockchain pour le calcul qui peut être fait hors chaîne (La théorie des jeux!).

En règle générale, 21 000 gaz sont facturés pour toute transaction à titre de « frais de base » pour couvrir le coût d’une opération de courbe elliptique pour calculer l’adresse de l’expéditeur à partir de la signature, ainsi que pour l’espace disque du stockage de la transaction. Il existe des moyens d’estimer les besoins en gas pour les transactions et les contrats.

Exemple : «estimateGas» est une fonction Web3 pour estimer les besoins en gas pour une fonction donnée. En outre, pour estimer le coût total, oracle prix du gaz est une fonction d’aide dans “geth” client et “web3.eth.getGasPrice” est une fonction native Web3 pour trouver un prix approximatif du gas. Voici un exemple de code qui peut être utilisé dans “Truffle”:

Exemple de code pour l’estimation des coûts de transaction

var MyContract = artifacts.require(“./MyTest.sol”);

// getGasPrice retourne le prix du gaz à Wei

MyContract.web3.eth.getGasPrice(function(error, result){

var gasPrice = Number(result);

console.log(“Current gasPrice is ” + gasPrice + ” wei”);

// Obtenez l’instance de contrat

MyContract.deployed().then(function(instance) {

// Récupérer l’estimation de gaz pour la fonction

giveAwayDividend()

return instance.giveAwayDividend.estimateGas(1);

}).then(function(result) {

var gas = Number(result);

console.log(“Total gas estimation = ” + gas + ” units”);

console.log(“Total Transaction Cost estimation in Wei =” + (gas *

gasPrice) + ” wei”);

console.log(“Total Transaction Cost estimation in

Ether = ” + MyContract.web3.fromWei((gas * gasPrice),

‘ether’) + ” Ether”);

});

});

Tout en écrivant des contrats intelligents dans Solidity, beaucoup préfèrent utiliser des fonctions «constantes» pour calculer certaines choses hors chaîne ou tout simplement faire une requête RPC à votre blockchain locale. Étant donné que ces fonctions constantes ne changent pas l’état de la blockchain, elles sont d’une manière libre de coût car elles ne consomment pas de gas. Si les fonctions constantes sont utilisées à l’intérieur de toute transaction, il est très probable que des dépenses en gas seraient nécessaires.

Détaillons maintenant la limite de gaz d’un bloc. Se rappeler que Bitcoin avait une limite prédéfinie de la taille du bloc de 1 Mo et que l’argent Bitcoin avait une taille de bloc de 2 Mo. Les mineurs accumuleraient autant de transactions que possible dans ces blocs. Ethereum, cependant, a une façon très différente de limiter la taille du bloc. Dans Ethereum, la taille du bloc est contrôlée par la limite de gas de bloc. Différentes transactions ont des limites de gas différentes; donc, selon la limite de gas de bloc, un certain nombre de transactions sont matraquées ensemble de sorte que la limite totale de gas de transactions est inférieure à la limite de gas d’un bloc. Différents mineurs peuvent avoir différents ensembles de transactions qu’ils sont prêts à mettre dans un bloc. La limite de gas de bloc est calculée dynamiquement. Le protocole Ethereum permet au mineur d’un bloc d’ajuster la limite de gas d’un bloc par un facteur de 1/1024 (0.0976%) dans les deux sens. Les mineurs du réseau Ethereum utilisent un programme minier, comme « ethminer ». L’ethminer est un travailleur minier Ethereum GPU, qui se connecte soit à geth ou Parity du noeud client. Le geth et la Parité ont des options que les mineurs peuvent changer.

Contrats intelligents Ethereum

Contrairement à Bitcoin, qui n’est qu’une crypto-monnaie, Ethereum est beaucoup plus grâce aux contrats intelligents. Nous avons eu un aperçu de ce qu’un contrat intelligent pourrait être dans les sections précédentes tout en apprenant sur les comptes de contrat. Bien que nous en nous acquiessons aux aspects de développement des contrats intelligents dans les chapitres suivants, nous aurons une exploration détaillée de ce qu’ils sont réellement dans cette section.

Commençons par pourquoi il est nommé ainsi?

Il faut être conscient qu’il n’y a rien d’ «intelligent» dans un contrat intelligent qui est « out-of-the-box ». Il est intelligent lorsque vous codez la logique intelligente en elle, et c’est la beauté de Ethereum qui vous permet de le faire. Résumons simplement notre apprentissage jusqu’à présent sur les contrats intelligents Ethereum :

• Les contrats intelligents résident à l’intérieur de la blockchain Ethereum.
• Ils ont leur propre compte, donc l’adresse et l’équilibre.
• Ils sont capables d’envoyer des messages et de recevoir des transactions.
• Ils sont activés lorsqu’ils reçoivent une transaction, et peuvent être désactivés ainsi.
• Comme d’autres transactions, des frais d’exécution et de stockage s’appliquent également à eux.

Tout le code d’Ethereum, y compris les contrats intelligents, est compilé selon un langage bytecode de faible niveau, basé sur la pile, appelé code EVM, qui s’exécute sur EVM. Les langues populaires de haut niveau utilisées pour écrire des contrats intelligents sont Solidity, Serpent et LLL, où leurs compilateurs respectifs convertissent le code de haut niveau dans le code octet EVM. Nous avons examiné comment des contrats pourraient être ajoutés à la blockchain par n’importe quel agent externe tel que EOA. Étant donné que le calcul et le stockage dans Ethereum sont très coûteux, il est conseillé que la logique doit être écrite de la manièrela plus simple et la plus optimisée que possible. Lorsqu’un contrat intelligent est déployé sur le réseau de blockchain Ethereum, il est possible pour quiconque d’appeler les fonctions du contrat intelligent. Les fonctions ont généralement des fonctions de sécurité codées qui empêchent l’accès non autorisé; néanmoins, des tentatives peuvent être faites bien qu’elles ne réussiront pas.

Si vous essayez d’imaginer un contrat intelligent à l’intérieur d’un bloc dans une blockchain Ethereum, il peut apparaître comme dans la figure 4-9.

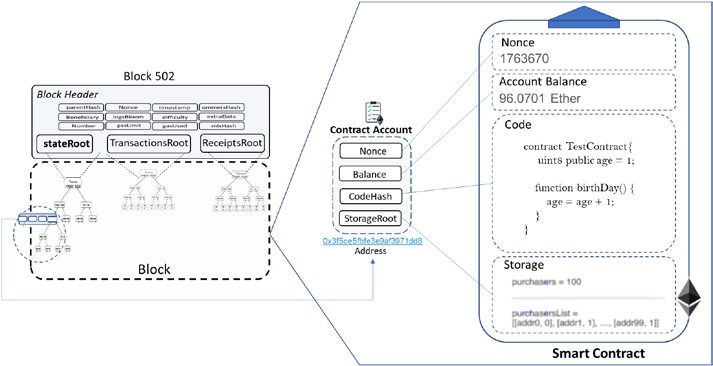
Figure 4-9. Contrat intelligent Ethereum en ce qui concerne les blocs

Prenons maintenant l’exemple d’une demande de vote. Un contrat intelligent est écrit a une adresse (adresse de compte de contrat) et fait partie d’un bloc dans la blockchain, selon le moment où il a été créé. Les électeurs peuvent effectuer des transactions à cette adresse (votes). Le code contractuel est écrit de telle sorte qu’il augmentera le nombre de voix avec chaque transaction reçue et se termine après un certain temps, en publiant le résultat du vote (changement d’état Ethereum). Jetez un coup d’œil à la figure 4-10 pour avoir une représentation schématique pour une compréhension de haut niveau.

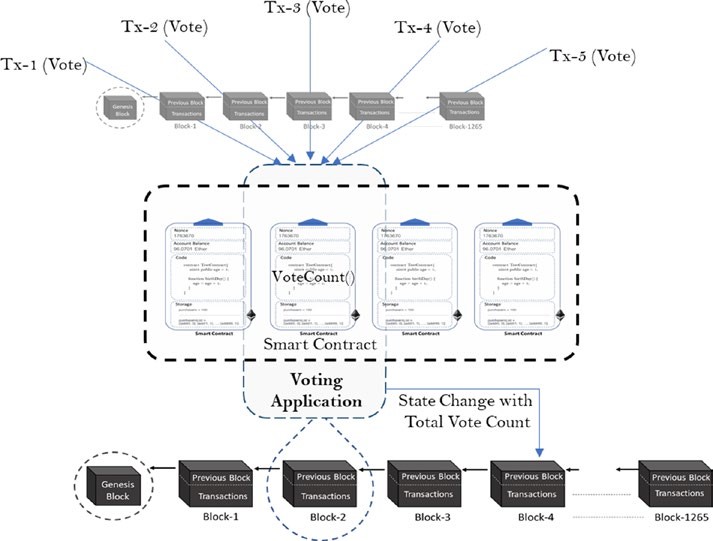
Figure 4-10. Une application avec une logique de contrat intelligente

Création de contrats

Rappelons que nous avons appris au sujet de la transaction de création de contrat, dont le seul but est de créer un contrat. C’est un type de transaction un peu différent par rapport aux autres types. Ainsi, avant que la transaction de création de contrat soit déclenchée pour créer un compte de contrat, elle doit d’abord initialiser les quatre propriétés que tous les types de comptes ont :

• Le “nonce” doit être réglé à zéro dans un premier temps.
• Le « Account Balance» doit être fixé avec la valeur (montant de l’éther) transférée par l’expéditeur, et le même montant doit être déduit du compte de l’expéditeur.
• Le “StorageRoot” doit être vide.
• Le “codeHash” du contrat doit être réglé avec le hachage Keccak 256 bits d’une chaîne vide.

Après l’initialisation du compte, le compte peut être créé à l’aide du code init envoyé avec la transaction qui fait le travail réel. Il pourrait y avoir tout un tas d’actions définies dans le code init, et son exécution peut effectuer plusieurs événements qui ne sont pas internes à l’état d’exécution, tels que:

• Le «stockage» du compte peut être modifié.
• D’autres comptes peuvent être créés.
• D’autres appels de messages peuvent être déclenchés.

Ethereum Virtual Machine et exécution de code

Ethereum est une blockchain programmable qui permet aux utilisateurs de créer leurs propres opérations de toute complexité arbitraire à travers des langues Turing-complètes. L’EVM est le moteur d’exécution d’Ethereum qui sert d’environnement de runtime pour les contrats intelligents. C’est l’innovation première d’Ethereum qui le rend unique par rapport à d’autres systèmes blockchain. C’est l’EVM sur la base de laquelle la technologie de contrat intelligent est censé passer au prochain niveau d’innovation, et le jeu est sur. EVM joue également un rôle essentiel dans l’exécution des transactions, en modifiant l’état d’Ethereum et en obtenant un consensus. Les objectifs de conception d’EVM sont les suivants :

• Simplicité : L’idée était de rendre EVM aussi simple que possible avec les constructions de bas niveau. C’est pourquoi le nombre d’opcodes de bas niveau est réduit au minimum, tout comme les types de données dans la mesure où les logiques pourraient encore être écrites commodément en utilisant ces constructions. Total 160 instructions, dont 65 sont logiquement distinctes
• Déterminisme absolu: S’assurer que l’exécution des instructions avec le même ensemble d’entrées devrait produire le même ensemble de sorties (déterministe!) contribue à maintenir l’intégrité de l’EVM sans aucune ambiguïté. Le déterminisme ainsi que le concept d’« étape computationnelle » aident à estimer les dépenses de gas avec une approximation étroite.
• Optimisation de l’espace : Dans les systèmes décentralisés, l’économie d’espace est une préoccupation majeure. C’est pourquoi l’assemblage EVM est maintenu aussi compact que possible.
• Ajusté pour les opérations natives : EVM est réglé pour certaines opérations natives telles que les types spécifiques d’opérations arithmétiques utilisées pour la cryptographie (arithmétique modulaire), les blocs de lecture ou les données de transaction, l’interaction avec les « états », etc. Un autre exemple est: 256 bits (32 octets) longueur de mot pour stocker des hachage cryptographiques, où EVM fonctionne sur le même 256 bits entier.
• Sécurité facile : D’une certaine manière, le prix du gas permet de s’assurer que l’EVM n’est pas exploitable. S’il n’y avait aucun coût, les attaquants pourraient simplement continuer à attaquer le système de toutes les manières possibles. Bien que presque toutes les opérations sur EVM nécessite un certain coût de gas, il devrait être facile de trouver un bon modèle de coût du gas sur EVM

Nous avons appris que chaque nœud participant au réseau Ethereum gère EVM localement, exécute toutes les transactions et les contrats intelligents, et enregistre l’état final localement. C’est l’EVM qui écrit le code (contrats intelligents), les données à la blockchain et exécute des instructions (opcodes) du code de transaction et du code de contrat intelligent écrits dans une langue Turing-complète. C’est-à-dire qu’EVM sert d’environnement de runtime (RTE) pour les contrats intelligents Ethereum et assure l’exécution sécurisée du code. Évidemment, lorsque le code ou les transactions sont validés par leurs signatures numériques respectives, ils sont exécutés sur EVM. Ainsi, ce n’est qu’après l’exécution réussie des instructions par l’intermédiaire d’EVM, que l’état Ethereum peut changer.

À moins que l’on ne connecte l’EVM avec le reste du réseau pour participer au réseau P2P, il peut être isolé du réseau principal. Dans un environnement isolé et saboté, EVM pourrait être utilisé pour tester des contrats intelligents. Il facilite la construction de meilleurs contrats, robustes et prêts à l’emploi.

Pour mieux comprendre comment les contrats intelligents fonctionnent en tirant parti de l’EVM, nous devons comprendre comment les données sont organisées, stockées et manipulées dans n’importe quelle langue EVM comme Solidity, Serpent, et ceux qui pourraient venir à l’avenir. Vous voudrez peut-être considérer EVM plus comme un moteur de base de données. Bien que nous n’allons pas aller plus loin dans les principes fondamentaux de la programmation Solidity, nous verrons comment il interagit avec l’EVM dans cette section. Jetez un coup d’œil à la figure 4-11.

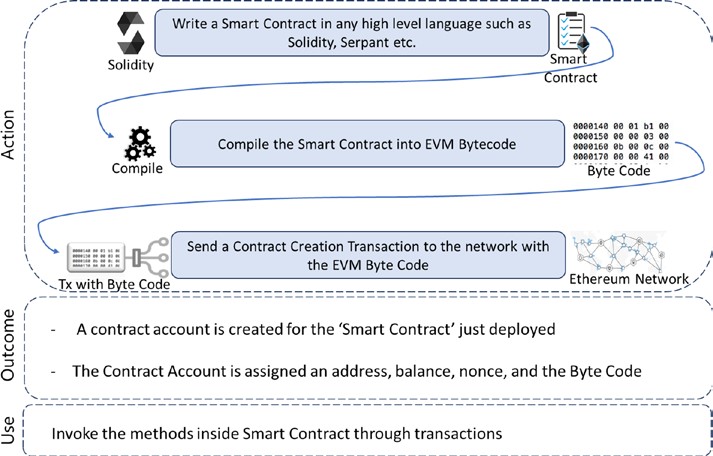
Figure 4-11. Déploiement et utilisation de contrats intelligents

Comprenons maintenant la gestion de la mémoire avec EVM. Jetez un coup d’œil aux trois stratégies suivantes :

• Stockage (persistant)
• Cartographie de stockage de valeur clé (c.-à-d. 256 bits à 256 bits de mappage de mots). Cela signifie que les touches et les valeurs sont de 256 bits (c’est-à-dire 32 octets).
• À partir d’un contrat, il n’est pas possible d’énumérer le stockage.
• À tout moment, l’état du contrat peut être déterminé par les variables de niveau du contrat appelées « variables d’état » qui sont toujours en « stockage », et il ne peut pas être mis à jour à l’exécution. Cela signifie que la structure du stockage n’est fixée qu’une seule fois pendant la création du contrat et ne peut pas être modifiée. Toutefois, leur contenu peut être modifié avec des appels “sendTransaction”.
• Lecture /mise à jour du stockage est une affaire coûteuse.
• Les contrats ne peuvent pas lire, écrire ou mettre à jour tout autre stockage qui n’en appartient pas.
• SSTORE/SLOAD sont les instructions fréquemment utilisées. Exemple : l’instruction SSTORE découpe les deux éléments supérieurs de la pile, considère le premier élément comme l’index et insère le deuxième élément dans le stockage du contrat à cet emplacement d’index.
• Mémoire (volatile)
• Il est similaire à l’exigence de RAM dans un système informatique général pour tout code ou exécution d’application et utilisé pour stocker des valeurs temporaires.
• Un contrat peut utiliser n’importe quelle quantité de mémoire pendant l’exécution en payant pour cela, et que l’espace de mémoire est nettoyé après l’exécution terminée. Les sorties pendant l’exécution pourraient être poussées au stockage persistant qui peut être réutilisé dans les exécutions futures.
• La mémoire est en fait un tableau d’octet qui est contigu, contrairement au stockage. Il est réparti en morceaux de 256 bits (32 octets).
• Commence sans espace et prend de l’espace dans les unités de morceaux de 32 octets.
• Sans le mot clé « mémoire », les langages contractuels intelligents tels que Solidity sont censés déclarer des variables en stockage pour la persistance.
• La mémoire ne peut pas être utilisée au niveau du contrat intelligent; il ne peut être utilisé que dans les méthodes.
• Les arguments de fonction sont presque toujours dans la mémoire.
• MSTORE/MLOAD sont les instructions fréquemment utilisées.
• Stack
• EVM est basé sur la pile, suit donc LIFO (Last in, First- Out), où la pile est utilisée pour effectuer des calculs.
• Les entrées de pile sont également des mots 256 bits utilisés pour imiter les registres pseudo 256 bits. Ils sont utilisés pour contenir des variables locales de type « valeur » et pour transmettre des paramètres aux instructions ou aux fonctions, aux opérations de mémoire et à d’autres opérations algorithmiques.
• Permet un maximum de 1024 élément et est presque libre d’utiliser.
• La plupart des opérations de pile sont limitées au sommet des piles. L’exécution est assez similaire à la façon dont le script Bitcoin a été exécuté.

Lorsque EVM est en cours d’exécution et que le code octet est injecté avec une transaction pour l’exécution, son état de calcul complet peut être défini par le tuple suivant : [block state, transaction, message, code, memory, stack, pc, gas]

Vous devez être en mesure de faire tous ces champs maintenant. Ils ont les trois types de mémoire dont nous avons discuté (le champ d’état de bloc représente l’état global et sert pour le stockage). Le champ PC est comme un pointeur pour une instruction dans la pile à exécuter.

Dans Ethereum, une interface binaire d’application (ABI) est une abstraction qui ne fait pas partie du protocole Ethereum de base, mais est utilisée pour accéder au code octet dans un contrat intelligent comme pratique standard. Bien qu’il soit possible pour quiconque de définir leur propre ABI pour leurs contrats et de s’y conformer pour obtenir la sortie désirée, il est plus facile d’utiliser Solidity. Le but de l’ABI est le suivant :

• Comment et quelles fonctions à l’intérieur des contrats intelligents devraient être appelés
• Le format binaire dans lequel l’information doit être transmise aux fonctions de contrat intelligents en tant qu’entrées
• Le format binaire dans lequel vous attendez la sortie de l’exécution de la fonction après avoir appelé cette fonction

Avec les spécifications ABI, il est facile (mais peut-être pas nécessaire) pour deux programmes écrits dans deux langues différentes d’interagir les uns avec les autres.

Écosystème Ethereum

Nous avons appris les composants de base pour comprendre comment Ethereum fonctionne vraiment. Il y a certaines limites inhérentes à Ethereum telles que ce qui suit :

• L’EVM est lent; il n’est pas consillé de l’utiliser pour de grands calculs.
• Le calcul et le stockage sur la blockchain sont coûteux; il est conseillé d’utiliser des calculs hors chaîne et d’utiliser IPFS/Swarm pour le stockage.
• L’évolutivité est un problème; il existe différentes techniques pour y remédier, mais elles sont subjectives à l’analyse de rentabilisation avec laquelle vous faites affaire.
• Les blockchains privées sont plus susceptibles de s’épanouir.

Jetons maintenant un coup d’œil à la pile technologique Ethereum pour comprendre à un niveau élevé l’écosystème Ethereum.

Swarm

Il ne s’agit pas seulement d’une plate-forme de stockage distribuée de fichiers statiques de manière P2P, mais aussi d’un service de distribution. Swarm assure une décentralisation adéquate et un stockage redondant des données blockchain d’Ethereum, du code DApp, etc.

Contrairement à WWW, les téléchargements sur Swarm ne sont pas centralisés vers un seul serveur Web. Il est conçu pour avoir zéro temps d’arrêt et est résistant à DDOS et tolérant aux défauts.

Whisper

Il s’agit d’un protocole de communication qui permet à DApps de communiquer entre eux. Il fournit une fonctionnalité de messagerie distribuée mais privée. Il prend en charge la distribution unique, multidiffusion et la diffusion de messages.

DApp

Un DApp a généralement deux composants, un front-end et un composant back-end. Le code back-end s’exécute sur la blockchain réelle codée dans des contrats intelligents. Le code frontal et les interfaces utilisateur peuvent être écrits dans n’importe quelle langue comme HTML, CSS et JavaScript, tant qu’il peut faire des appels à son back end. En outre, l’extrémité avant peut être hébergée dans un stockage décentralisé comme SWARM ou IPFS au lieu d’un serveur Web centralisé.

Les composants de l’interface utilisateur seront mis en cache sur une sorte de nuage décentralisé de type BitTorrent et entraînés par le navigateur Dapp au besoin. Comme n’importe quel App Store, il est possible de parcourir le catalogue DApps distribué dans le navigateur. L’utilisateur final peut installer n’importe quel DApp d’intérêt dans son navigateur.

Composants de développement

Il y a tellement de composants de développement utilisés pour développer des applications décentralisées sur Ethereum et interagir avec eux. Voici quelques-uns populaires, mais il y a beaucoup plus pour vous d’explorer. Nous allons simplement jeter un oeil à ce qu’ils sont et plonger plus profondément dans ces sujets dans les chapitres suivants.

Web3.js

Il s’agit d’un élément très important dans le développement de DApps.

Truffle

Truffle fournit les éléments constitutifs pour créer, compiler, déployer et tester des applications blockchain.

Mist Wallet

Nous avons appris dans les chapitres précédents qu’un portefeuille est nécessaire pour interagir avec les applications blockchain et la même chose s’applique à Ethereum ainsi.

Pour stocker, accepter et envoyer Ether, les utilisateurs ont besoin d’un portefeuille. Mist Wallet est une solution basée sur l’interface qui peut être utilisée pour se connecter à la blockchain Ethereum. À l’aide d’un portefeuille Mist, on peut créer des comptes, concevoir et déployer des contrats, transférer de l’Ether sur les comptes et afficher les détails de la transaction.

En interne, Mist dépend du client “geth” (c’est-à-dire, GoEthereum Client) pour effectuer toutes les opérations de manière transparente.

Résumé

Dans ce chapitre, nous avons couvert les composants de base de la blockchain Ethereum et compris les considérations de conception. Nous avons pu différencier la conception d’Ethereum avec celle de la blockchain Bitcoin et comprendre comment la blockchain Ethereum facilite le développement de différents cas d’utilisation sur une seule plate-forme. Nous avons étudié les contrats intelligents et la façon dont la machine virtuelle Ethereum (EVM) l’exécute de manière décentralisée.

Nous allons explorer davantage l’aspect développement de la blockchain en général dans le chapitre 5, puis construire une solide compréhension du développement ethereum dans le chapitre 6.

CHAPITRE 5 : Développement d’applications avec la BlockChain

Dans les chapitres précédents, nous sommes entrés dans les détails théoriques sur ce qu’est la blockchain et comment les blockchains Bitcoin et Ethereum fonctionnent. Nous avons également examiné les différents algorithmes cryptographiques et mathématiques, les théorèmes et les preuves qui entrent dans la fabrication de la technologie blockchain.

Dans ce chapitre, nous allons commencer par la façon dont les applications blockchain sont différentes des applications conventionnelles, puis nous allons plonger dans la façon de construire des applications sur les blockchains. Nous examinerons également la mise en place de l’infrastructure nécessaire pour commencer à développer des applications décentralisées.

Applications décentralisées

La popularité de la technologie blockchain est principalement motivée par le fait qu’elle peut potentiellement résoudre divers problèmes du monde réel, car elle offre plus de transparence et de sécurité que les technologies conventionnelles. Il y a beaucoup de cas d’utilisation blockchain identifiés par plusieurs Startup et les membres de la communauté visant à résoudre ces problèmes.

Pour implémenter ces cas d’utilisation, nous créons des applications qui fonctionnent au-dessus des blockchains. En général, les applications qui interagissent avec les blockchains sont appelées « applications décentralisées » ou, en bref, simplement DApps ou dApps.

Pour mieux comprendre DApps, revoyons d’abord ce qu’est une blockchain. Une blockchain ou un grand livre distribué est essentiellement un type spécial de base de données où les données ne sont pas stockées sur un serveur centralisé, mais elles sont copiées à tous les nœuds participants dans le réseau. En outre, les données sur les blockchains sont cryptographiques signés, ce qui prouve l’identité de l’entité qui a écrit ces données sur la blockchain. Pour utiliser cette base de données pour stocker et récupérer des données, nous créons des applications appelées DApps parce que ces applications ne reposent pas sur une base de données centralisée mais sur une blockchain-basée sur un magasin de données décentralisées. Il n’y a pas de point de défaillance ou de contrôle unique pour ces applications.

Prenons l’exemple d’un DApp. Prenons un scénario de chaîne d’approvisionnement où plusieurs fournisseurs et partenaires logistiques sont impliqués dans le processus de la chaîne d’approvisionnement des produits manufacturés. Pour utiliser la technologie blockchain pour ce cas d’utilisation de la chaîne d’approvisionnement, voici ce que nous pourrions faire :

• Nous aurions besoin de mettre en place des nœuds blockchain à chacun de ces fournisseurs afin qu’ils puissent participer au processus de consensus sur les données partagées.
• Nous aurions besoin d’une interface pour que tous les participants et utilisateurs puissent stocker, récupérer, vérifier et évaluer les données sur la blockchain. Cette interface serait utilisée par le fabricant pour entrer les informations sur les marchandises fabriquées ; par le partenaire logistique pour saisir des informations sur le transfert de marchandises ; par le fournisseur de stockage pour vérifier si les marchandises fabriquées et les marchandises transférées sont synchronisées, etc., etc. Cette interface serait notre chaîne d’approvisionnement DApp.

Un autre exemple d’un DApp serait un système de vote basé sur les blockchains. En utilisant la blockchain pour voter, nous serions en mesure de rendre l’ensemble du processus beaucoup plus transparent et sécurisé parce que chaque vote serait cryptographiquement signé. Nous aurions besoin de créer une application qui pourrait obtenir une liste de candidats pour lesquels les électeurs pourraient voter, et cette demande fournirait également une interface simple pour soumettre et enregistrer les votes.

Développement d’applications Blockchain

Avant de sauter dans le code, nous allons d’abord comprendre quelques concepts de base. En général, nous sommes habitués à des concepts comme des objets, des classes, des fonctions, etc lorsque nous développons des applications logicielles conventionnelles. Cependant, quand il s’agit d’applications blockchain, nous avons besoin de comprendre un peu plus de concepts comme les transactions, les comptes et les adresses, jetons et portefeuilles, entrées, et les sorties et les soldes. Le mécanisme de contact et de demande/réponse entre une application décentralisée et une blockchain sont pilotés par ces concepts.

Tout d’abord, lors du développement d’une application basée sur la blockchain, nous devons identifier comment les données de l’application serait cartographié au modèle de données blockchain. Par exemple, lors du développement d’une DApp sur la blockchain Ethereum, nous devons comprendre comment l’état d’application peut être représenté en termes de structures de données Solidity et comment le comportement de l’application peut être exprimé en termes de contrats intelligents Ethereum. Comme nous savons que toutes les données d’une blockchain sont cryptographiques signées par des clés privées des utilisateurs, nous devons identifier les entités de notre application qui auraient des identités ou des adresses représentées sur la blockchain. Dans les applications conventionnelles, ce n’est généralement pas le cas, car les données ne sont pas toujours signées. Pour l’application blockchain, nous devons définir qui seraient les signataires et quelles données ils signeraient. Par exemple, dans un DApp de vote dans lequel chaque électeur signe cryptographiquement leur vote, c’est facile à identifier. Cependant, imaginons un scénario où nous devons migrer une application de systèmes distribués conventionnels existants, ayant ses données stockées à travers plusieurs tables SQL et bases de données, à un DApp basé sur la blockchain Ethereum. Dans ce cas, nous devons identifier les entités dans lesquelles le tableau aurait leur identité et quelles entités seraient attachées à d’autres identités.

Dans les prochaines sections, nous explorerons la programmation d’applications Bitcoin et Ethereum à l’aide de simples extraits de code pour envoyer certaines transactions. Le but de cet exercice est de se familiariser avec les API blockchain et les pratiques de programmation courantes. Pour plus de simplicité, nous utiliserons des réseaux de test publics pour ces blockchains et nous écrirons du code dans JavaScript. La raison de la sélection de JavaScript est, au moment de cette écriture, la disponibilité de bibliothèques JavaScript stables pour les deux blockchains et il sera plus facile de comprendre les similitudes et les différences dans les approches que nous prendrons lors de l’écriture de code. Les extraits de code sont expliqués en détail après chaque étape logique et peuvent être compris même si le lecteur n’est pas familier avec la programmation JavaScript.

Bibliothèques et outils

Rappelez-vous du chapitre 2, qu’il y a beaucoup d’algorithmes cryptographiques et les mathématiques utilisées dans la technologie blockchain. Avant d’envoyer nos transactions aux blockchains à partir d’une application, nous devons les préparer. La préparation de la transaction comprend la définition des comptes et des adresses, l’ajout des paramètres et des valeurs requis aux objets de transaction, et la signature à l’aide de clés privées, entre autres choses. Lors du développement d’applications, il est préférable d’utiliser des bibliothèques vérifiées et testées pour la préparation des transactions au lieu d’écrire du code à partir de zéro. Certaines des bibliothèques stables pour Bitcoin et Ethereum sont disponibles open source, qui peut être utilisé pour préparer et signer des transactions et de les envoyer aux nœuds blockchain / réseau. À la fin de nos exercices de code, nous utiliserons la bibliothèque Bitcoinjs JavaScript pour interagir avec la blockchain Bitcoin et la bibliothèque JavaScript web3.js pour interagir avec la blockchain Ethereum. Ces deux bibliothèques sont disponibles sous forme de paquets node.js et peuvent être téléchargées et intégrées à l’aide des commandes npm.

Les exercices de code dans ce chapitre sont basés sur les applications node.js. C’est pour s’assurer que le code que nous écrivons dans le cadre de cet exercice a un conteneur dans lequel il peut fonctionner et interagir avec les autres bibliothèques préemballées mentionnés. il est agréable d’avoir une certaine connaissance sur le développement de l’application node.js, et le lecteur est encouragé à suivre un tutoriel de démarrage sur node.js et npm.

La Figure 5-1 montre comment un DApp interagit avec une blockchain.

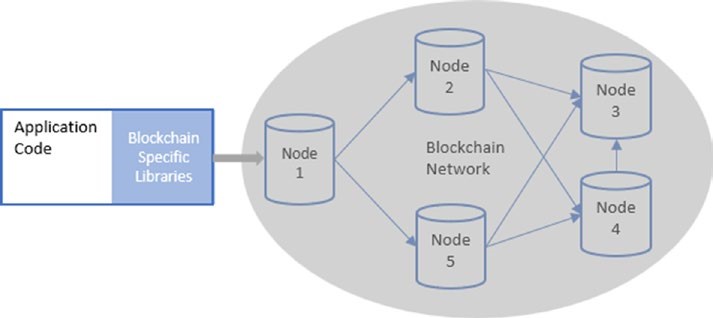
Figure 5-1. Interaction d’application Blockchain

Interagir avec la Blockchain Bitcoin

Dans cette section, nous enverrons une transaction au réseau de test public Bitcoin d’une adresse à l’autre. Considérez cela comme une application “Hello World” pour la blockchain Bitcoin. Comme mentionné précédemment, nous utiliserons la bibliothèque JavaScript bitcoinjs pour la préparation et la signature des transactions. Et pour plus de simplicité, au lieu d’héberger un nœud Bitcoin local, nous utiliserons un nœud public de réseau de test Bitcoin hébergé par un fournisseur tiers block-explorer. Vous pouvez utiliser n’importe quel fournisseur pour votre application et vous pouvez également héberger un nœud local. Tout ce que vous devez faire est de pointer votre code d’application pour se connecter à votre nœud préféré.

Rappelez-vous des chapitres précédents que la blockchain Bitcoin est principalement pour permettre des paiements peer to peer. Une transaction Bitcoin n’est pour la plupart qu’un transfert de Bitcoins d’une adresse à l’autre. Voici comment nous faisons cela programmatiquement.

Ce qui suit (figure 5-2) montre comment ce code interagit avec la blockchain Bitcoin.

La figure est juste une esquisse approximative et ne montre pas l’architecture de service Block Explorer en détail.

Figure 5-2. Application interagissant avec la blockchain Bitcoin à l’aide de l’API Block Explorer

Les sous-titres suivants de cette section sont des étapes à suivre, dans cet ordre, pour envoyer une transaction au réseau de test Bitcoin en utilisant JavaScript.

Configurer et initialiser la bibliothèque bitcoinjs dans une application node.js

Avant d’appeler le code spécifique à la bibliothèque pour les transactions Bitcoin, nous installerons et initialiserons la bibliothèque bitcoinjs.

Après l’initialisation d’une application node.js à l’aide de la commande init npm, nous créons un point d’entrée pour notre application, index.js, et le module JavaScript personnalisé pour appeler les fonctions de la bibliothèque bitcoinjs btc.js. Import btc.js dans l’index.js . Maintenant, nous sommes prêts à suivre les prochaines étapes.

Tout d’abord, installons le module de nœud pour bitcoinjs:

npm install –save bitcoinjs-lib

Ensuite, dans notre module Bitcoin btc.js, nous allons initialiser la bibliothèque bitcoinjs en utilisant le mot clé exige:

var btc = require(‘bitcoinjs-lib’) ;

Maintenant, nous pouvons utiliser cette variable btc pour appeler les fonctions de bibliothèque sur la bibliothèque bitcoinjs. De plus, dans le cadre du processus d’initialisation, nous initialisons quelques variables de plus :

• Le réseau à cibler : Nous utilisons le réseau de test Bitcoin.

var network = btc.networks.testnet

• Le point de terminaison aPI de nœud public pour obtenir et poster des transactions : Nous utilisons l’API Block Explorer pour le réseau de test Bitcoin. Notez que vous pouvez remplacer ce point de terminaison API par votre point de terminaison préféré.

var blockExplorerTestnetApiEndpoint =’https://testnet.blockexplorer.com/api/’;

À ce stade, nous sommes tous mis en place pour créer une transaction Bitcoin en utilisant une application node.js.

Créer des keypairs pour l’expéditeur et le récepteur

La première chose dont nous aurons besoin sont les keypairs pour l’expéditeur et les récepteurs. Ce sont comme des comptes d’utilisateurs identifiant les utilisateurs sur la blockchain. Donc, nous allons d’abord créer deux keypairs pour Alice et Bob.

var getKeys = function () {

var aliceKeys = btc.ECPair.makeRandom({

network: network

});

var bobKeys = btc.ECPair.makeRandom({

network: network

});

var alicePublic = aliceKeys.getAddress();

var alicePrivate = aliceKeys.toWIF();

var bobPublic = bobKeys.getAddress();

var bobPrivate = bobKeys.toWIF();

console.log(alicePublic, alicePrivate, bobPublic, bobPrivate);

};

Ce que nous avons fait dans l’extrait de code précédent est l’utilisation de la classe ECPair de la bibliothèque bitcoinjs et appelé la méthode makeRandom sur elle pour créer des keypairs aléatoires pour le réseau de test; notez le paramètre passé pour le type de réseau.

Maintenant que nous avons créé un couple de keypairs, nous allons les utiliser pour envoyer Bitcoins de l’un à l’autre. Dans presque tous les exemples de cryptographie, Alice et Bob ont été les personnages préférés, comme on le voit dans les variables keypair précédentes. Cependant, chaque fois que nous voyons un exemple de cryptographie, en général Alice est celle qui crypte / signe quelque chose et envoie à Bob.

Pour cette raison, nous pensons que Bob est très endetté vis-à-vis d’Alice, donc dans notre cas, nous allons aider Bob à rembourser une partie de cette dette. Nous ferons cet exemple de transaction Bitcoin de Bob à Alice.

Obtenez des Bitcoins de test dans le portefeuille de l’expéditeur

Nous avons identifié que Bob va agir en tant qu’expéditeur dans cet exemple de transaction Bitcoin. Avant d’envoyer des Bitcoins à Alice, il doit les posséder. Comme nous savons que cette transaction par exemple vise le réseau de test Bitcoin, il n’y a pas d’argent réel en jeu, mais nous avons encore besoin de Bitcoins test dans le portefeuille de Bob. Une façon simple d’obtenir bitcoins de test est de demander sur Internet. Il y a beaucoup de sites Web sur Internet qui hébergent un formulaire Web simple pour prendre les adresses Bitcoin testnet et ensuite envoyer des Bitcoins net de test. Ces services sont appelés Bitcoin testnet faucets, et si vous recherchez en ligne pour ce terme, vous obtiendrez beaucoup de résultats de recherche. Nous n’énumérons pas ou ne recommandons aucun d’entre eux spécifiquement parce qu’ils ne sont généralement pas permanents. Dès qu’un fournisseur de services de faucets a épuisé leurs coins d’essai, ou qu’ils ne veulent plus héberger le service, ils arrêtent. Mais alors de nouveaux continuent à se créer en permanences. Une liste de certains de ces services de faucet est également disponible sur la page Bitcoin wiki testnet.

Le minage de blocs sur le réseau de test Bitcoin n’est pas aussi difficile que celle du réseau principal. Cette approche pourrait bien être l’approche de « nest level » lorsque vous construisez une application Bitcoin de production et que vous devez la tester fréquemment. Au lieu de demander des pièces de test chaque fois que vous voulez tester votre application, vous pouvez simplement les exploiter vous-même.

Pour les besoins de cet exemple simple, nous allons juste obtenir quelques Bitcoins à partir d’un faucet testnet. Dans l’extrait de code précédent, la valeur de la variable bobPublic est l’adresse de Testnet Bitcoin de Bob. Lorsque nous avons fait cet extrait, il a généré “msDkUzzd69idLLGCkDFDjVRz44jHcV3pW2” comme adresse pour Bob. C’est aussi une clé pubique encodée sur la base 58. Nous soumettrons cette valeur dans l’un des formulaires web de faucet de testnet et en retour nous recevrons un ID de transaction. Si nous recherchons cet ID de transaction sur l’un des explorateurs bitcoin testnet, nous verrons qu’une autre adresse a envoyé quelques Bitcoins de test à l’adresse de Bob que nous avons soumis dans le formulaire.

Obtenez les sorties non dépensées de l’expéditeur

Maintenant que nous savons que nous avons des Bitcoins de test dans le portefeuille de Bob, nous pouvons les dépenser et les donner à Alice par le biais d’une transaction Bitcoin. Rappelons-nous dans le chapitre 3 comment les transactions Bitcoin sont effectuées d’entrées et de sorties. Vous pouvez dépenser vos extrants non dépensés en les ajoutant comme entrées aux transactions où vous souhaitez les dépenser. Pour ce faire, vous devez d’abord interroger le réseau sur les sorties non dépensées de l’expéditeur. Voici comment nous allons le faire pour l’adresse Bitcoin testnet de Bob en utilisant l’API d’explorateur de bloc. Pour obtenir les sorties non dépensées, nous enverrons une demande HTTP au point de terminaison UTXO avec l’adresse de Bob “msDkUzzd69idLLGCkDFDjVRz44jHcV3pW2”.

var getOutputs = function () {

var url = blockExplorerTestnetApiEndpoint + ‘addr/’ +

msDkUzzd69idLLGCkDFDjVRz44jHcV3pW2 + ‘/utxo’;

return new Promise(function (resolve, reject) {

request.get(url, function (err, res, body) {

if (err) {

reject(err);

}

resolve(body);

});

});

};

Dans l’extrait de code précédent, nous avons utilisé le module de demande de node.js pour envoyer des demandes http à l’aide d’une application node.js. N’hésitez pas à utiliser votre bibliothèque http/module préférée. Cet extrait est une fonction JavaScript qui renvoie une promesse qui résout dans le corps de réponse de la méthode API. Voici à quoi ressemble la réponse :

[

{

adresse: ‘msDkUzzd69idLLGCkDFDjVRz44jHcV3pW2’, txid: ‘db2e5966c5139c6e937203d567403867643482bbd9a6624752bbc583ca259958’,

vout: 0,

scriptPubKey: ’76a914806094191cbd4fcd8b4169a70588ad c51dc02d6888ac’,

amount: 0.99992,

satoshis: 99992000,

height: 1258815,

confirmations: 1011

},

{

adresse: ‘msDkUzzd69idLLGCkDFDjVRz44jHcV3pW2’,

txid:’5b88d5fc467586b0a3a7fc5a36df9c425c3880a7453e3afeb4934e6d1d928e’, vout: 1,

scriptPubKey: ’76a914806094191cbd4fcd8b4169a70588ad c51dc02d6888ac’,

amount: 0.99998,

satoshis: 99998000,

height: 1258814,

confirmations: 10122

}

]

Le corps de réponse retourné par l’appel est un tableau JSON avec deux objets. Chacun de ces objets représente une sortie non dépensée pour Bob. Chaque sortie a txid, qui est l’ID de transaction où cette sortie est répertoriée, le montant associé à la sortie, et le vout, ce qui correspond à la séquence ou au numéro d’index de la sortie dans cette transaction. Il y a aussi d’autres informations dans les objets JSON, mais elles ne seront pas utilisées dans le processus de préparation des transactions.

Si nous prenons le premier objet dans le tableau, il dit essentiellement que l’adresse Bitcoin testnet “msDkUzzd69idLLGCkDFDjVRz44jHcV3pW2” a‘99992000‘ satoshis non dépensés en provenance de la transaction ‘db2e596c5139c6e937203d56740386764482bbd9a6624752bbc583c a259958‘ à l’indice ‘0 ‘. De même, le deuxième objet représente ‘99998000‘ satoshis non dépensés provenant de la transaction ‘5b88d5fc4675bb86b0a3a7fc5a36df9c425c3880a7453e3afeb4934 e6d1d928e‘ à l’indice ‘1‘.

N’oubliez pas que “msDkUzzd69idLLGCkDFDjVRz44jHcV3pW2” est le testnet Bitcoin de Bob, que nous avons créé à l’étape 2 plus tôt. Maintenant, nous savons que Bob a autant de satoshis, qu’il peut dépenser dans une nouvelle transaction.

Préparer la transaction Bitcoin

L’étape suivante consiste à préparer une transaction Bitcoin dans laquelle Bob peut envoyer les pièces de test à Alice. La préparation de la transaction consiste essentiellement à définir ses entrées, ses extrants et son montant.

Comme nous le savons de l’étape précédente que Bob a deux sorties non dépensées sous son adresse Bitcoin testnet, passons le premier élément du tableau des sorties. Ajoutons ceci comme entrée à notre transaction.

var utxo = JSON.parse(body.toString());

var transaction = new btc.TransactionBuilder(network);

transaction.addInput(utxo[0].txid, utxo[0].vout);

Dans l’extrait de code précédent, nous avons d’abord analysé la réponse que nous reçu de l’appel d’API précédent pour obtenir les sorties inutilisées de Bob.

Ensuite, nous avons créé un objet générateur de transactions pour le test Bitcoin réseau en utilisant la bibliothèque bitcoinjs.

Dans la dernière ligne, nous avons défini une entrée de transaction. Notez que cette entrée fait référence à l’élément à 0 index du tableau utxo, que nous avons reçu dans l’appel d’API de l’étape précédente. Nous avons transmis l’ID de transaction (txid) et vout de la méthode non dépensée à la méthode transaction.addInput comme paramètres d’entrée.

Ensuite, nous avons créé un objet de constructeur de transactions pour le réseau de test Bitcoin en utilisant la bibliothèque bitcoinjs.

Dans la dernière ligne, nous avons défini une entrée de transaction. Notez que cette entrée se réfère à l’élément à l’indice 0 du tableau utxo, que nous avons reçu dans l’appel API de l’étape précédente. Nous avons passé l’ID de transaction (txid) et le vout de la méthode non dépensée à la méthode transaction.addInput comme paramètres d’entrée.

Fondamentalement, nous définissons ce que nous voulons dépenser et d’où nous l’avons obtenu.

Ensuite, nous ajoutons les sorties de transaction. C’est là que nous disons comment nous voulons dépenser ce que nous avons ajouté dans l’entrée. Dans la ligne suivante, nous avons ajouté une sortie de transaction en appelant la méthode addOutput sur l’objet de constructeur de transaction et passé dans l’adresse cible et le montant. Bob veut envoyer 99990000 satoshis à Alice. Notez que nous avons utilisé l’adresse Bitcoin d’Alice comme premier paramètre de la fonction.

transaction.addOutput(alicePublic, 99990000);

Bien que nous n’ayons utilisé qu’une seule entrée et une seule sortie dans cette transaction par exemple, une transaction peut avoir plusieurs entrées et sorties. Une chose importante à noter est que le montant total des intrants ne doit pas être inférieur au montant total dans les extrants. La plupart du temps, le montant des intrants est légèrement supérieur au montant des extrants, et la différence est la taxe de transaction offerte aux mineurs pour inclure cette transaction lorsqu’ils extraient le bloc suivant.

Dans cette transaction, nous avons 2 000 satoshis pour la transaction, ce qui est la différence entre le montant des entrées (99992000) et le montant de la production (99990000). Nous n’avons pas à créer de sorties pour les frais de transaction ; la différence entre les montants totaux d’entrée et de sortie est automatiquement prise comme frais de transaction.

Nous ne pouvons pas dépenser des sorties partielles non dépensées. Si une sortie non dépensée a x quantité de Bitcoins qui lui sont associés, nous devons dépenser tous les X Bitcoins lors de l’ajout de cette sortie non dépensée comme entrée dans une transaction. Donc, au cas où Bob ne veut pas donner tous les 99 990 000 satoshis associés à sa sortie non dépensée à Alice, alors nous devons le rendre à Bob en ajoutant une autre sortie à la transaction avec un montant égal à la différence du montant total non dépensé et le montant bob veut donner à Alice.

Entrées de transaction de signe

Maintenant que nous avons défini les entrées et les sorties dans la transaction, nous devons signer les entrées en utilisant les clés de Bob. La ligne de code suivante appelle la fonction sign sur l’objet de constructeur de transaction pour signer cryptographiquement la transaction en utilisant la clé privée de Bob, mais il prend l’objet de paire de clés entier comme un paramètre d’entrée.

transaction.sign(0, bobKeys);

Notez que la fonction transaction.sign prend l’index de l’entrée et la paire de clé complète comme paramètres d’entrée. Dans cette transaction, parce que nous n’avons qu’une seule entrée, l’index que nous avons passé est de 0.

À ce stade, notre transaction est préparée et signée.

Créer Transaction Hex

Maintenant, nous allons créer une chaîne hexagonale à partir de l’objet transactionnel.

var transactionHex = transaction.build().toHex();

La sortie de cette ligne de code est la chaîne suivante, qui représente notre transaction préparée ; cette étape est nécessaire parce que l’API de transaction d’envoi accepte la transaction brute comme une chaîne.

Transaction de diffusion au réseau

Enfin, nous utilisons la valeur de chaîne hexagonale que nous avons générée dans la dernière étape et l’envoyons à l’explorateur de bloc noeud testnet public en utilisant l’API,

var txPushUrl = blockExplorerTestnetApiEndpoint + ‘tx/send’;

request.post({

url: txPushUrl,

json: {

rawtx: transactionHex

}

}, function (err, res, body) {

if (err) console.log(err);

console.log(res);

console.log(body);

});

Si la transaction est acceptée par le nœud public de l’explorateur de bloc, nous recevrons un ID de transaction comme réponse de cet appel API,

{

txid: “db2e5966c5139c6e937203d56740386764

3482bbd9a624752bbc583ca259958″

}

Maintenant que nous avons l’ID de transaction de notre transaction, nous pouvons le rechercher sur n’importe lequel des explorateurs de testnet en ligne pour voir si et quand il est extrait et combien de confirmations il a.

En mettant tout cela ensemble, voici le code complet pour l’envoi d’une transaction Bitcoin testnet en utilisant JavaScript. Les paramètres d’entrée sont les keypairs Bitcoin testnet que nous avons créés à l’étape 1.

var createTransaction = function (aliceKeys, bobKeys) {

getOutputs(bobKeys.getAddress()).then(function (res) {

var utxo = JSON.parse(res.toString());

var transaction = new btc.TransactionBuilder(network);

transaction.addInput(utxo[0].txid, utxo[0].vout);

transaction.addOutput(alicekeys.getAddress(),

99990000);

transaction.sign(0, bobKeys);

var transactionHex = transaction.build().toHex();

var txPushUrl = blockExplorerTestnetApiEndpoint +

‘tx/send’;

request.post({

url: txPushUrl,

json: {

rawtx: transactionHex

}

}, function (err, res, body) {

if (err) console.log(err);

console.log(res);

console.log(body);

});

});

};

Dans cette section, nous avons appris comment nous pouvons envoyer une transaction programmatiquement au réseau de test Bitcoin. De même, nous pouvons envoyer des transactions au réseau principal Bitcoin en utilisant le réseau principal comme cible dans les fonctions de la bibliothèque et dans les points de terminaison de l’API. Nous avons également utilisé les API de requête pour obtenir les sorties non dépensées d’une adresse Bitcoin. Ces fonctions peuvent être utilisées pour créer une simple application de portefeuille Bitcoin pour interroger et gérer les adresses et transactions Bitcoin.

Interagir programmatiquement avec Ethereum—Envoi de transactions

La blockchain Ethereum a beaucoup plus à offrir par rapport à la blockchain Bitcoin. La possibilité d’exécuter la logique sur la blockchain à l’aide de contrats intelligents est la caractéristique clé de la blockchain Ethereum qui permet aux développeurs de créer des applications décentralisées. Dans cette section, nous apprendrons à interagir programmatiquement avec la blockchain Ethereum à l’aide de JavaScript. Nous examinerons les principaux aspects de la programmation d’applications Ethereum, des transactions simples à la création et à l’appel de contrats intelligents.

Comme nous l’avons fait pour interagir avec la blockchain Bitcoin dans la section précédente, nous allons utiliser une bibliothèque JavaScript et un réseau de test pour interagir avec Ethereum ainsi. Nous utiliserons la bibliothèque JavaScript web3 pour Ethereum. Cette bibliothèque enveloppe un grand nombre d’API Ethereum JSON RPC et fournit des fonctions faciles à utiliser pour créer Ethereum DApps en utilisant JavaScript. Au moment de la rédaction, nous utilisons une version supérieure et compatible avec la version 1.0.0-beta.28 de la bibliothèque JavaScript web3.

Pour le réseau de test, nous utiliserons le réseau de test Ropsten pour la blockchain Ethereum.

Pour plus de simplicité, nous utiliserons à nouveau un nœud de réseau de test hébergé par le public pour Ethereum afin que nous n’ayons pas à héberger un nœud local pendant l’exécution de ces extraits de code. Cependant, tous les extraits devraient fonctionner avec un nœud hébergé localement. Nous utilisons les API Ethereum fournies par le service Infura. Infura est un service qui fournit des nœuds Ethereum hébergés par le public afin que les développeurs puissent facilement tester leurs applications Ethereum. Il y a une petite étape d’inscription gratuite nécessaire avant que nous puissions utiliser l’API d’Infura, donc nous irons à https://infura.io et faire une inscription. Nous obtiendrons une clé API après l’enregistrement. En utilisant cette clé API, nous pouvons maintenant appeler l’API Infura.

Ce qui suit (figure 5-3) montre comment ce code interagit avec la blockchain Ethereum.

La figure est juste une esquisse approximative et ne montre pas l’architecture de service Infura en détail.

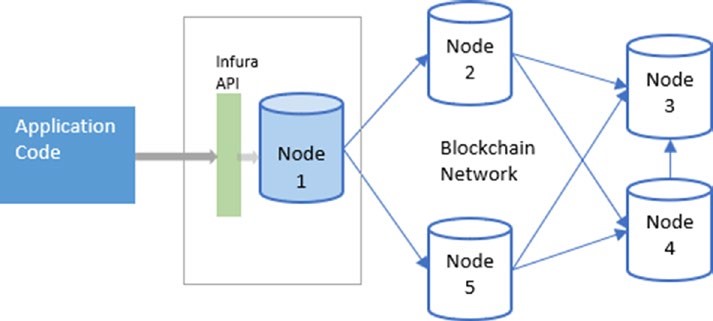
Figure 5-3. Application interagissant avec la blockchain Ethereum à l’aide Service API Infura

Les sous-sections suivantes de cette section sont des étapes à suivre, dans cet ordre, pour envoyer une transaction au réseau de test Ethereum Ropsten à l’aide de JavaScript.

Configurer la bibliothèque et la connexion

Tout d’abord, nous installons la bibliothèque web3 dans notre application node.js. Notez la version spécifique de la bibliothèque mentionnée dans la commande d’installation. C’est parce que la version 1.0.0 de la bibliothèque a quelques API et fonctions disponibles et ils réduisent la dépendance à d’autres paquets externes.

npm installer web3@1.0.0-bêta.28

Ensuite, nous initialisons la bibliothèque dans notre module Nodejs Ethereum en utilisant le mot clé de besoin,

var Web3 = require(‘web3’);

Maintenant, nous avons une référence de la bibliothèque web3, mais nous devons l’instantier avant de pouvoir l’utiliser. La ligne de code suivante crée une nouvelle instance de l’objet Web3 et il définit le nœud réseau de test Ethereum Ropsten hébergé par Infura en tant que fournisseur de cette instance Web3.

var web3 = new Web3(new Web3.providers.HttpProvider(‘https:// ropsten.infura.io/<your Infura API key>’));

Configurer des comptes Ethereum

Maintenant que nous sommes tous mis en place, nous allons envoyer une transaction à la blockchain Ethereum. Dans cette transaction, nous enverrons un peu d’éther d’un compte à l’autre. Rappelons au chapitre 4 qu’Ethereum n’utilise pas le modèle UTXO mais qu’il utilise un modèle de compte et d’équilibres.

Fondamentalement, la blockchain Ethereum gère l’État et les actifs en termes de comptes et de soldes, tout comme les banques. Il n’y a pas d’entrées et de sorties ici. Vous pouvez simplement envoyer Ether d’un compte à l’autre et Ethereum s’assurera que les états sont mis à jour pour ces comptes sur tous les nœuds.

Pour envoyer une transaction à Ethereum qui transfère Ether d’un compte à l’autres, nous aurons d’abord besoin d’un couple de comptes Ethereum. Commençons par créer deux comptes pour Alice et Bob.

L’extrait de code suivant appelle la fonction de création de compte de la bibliothèque web3 et crée deux comptes.

var createAccounts = function () {

var aliceKeys = web3.eth.accounts.create();

console.log(aliceKeys);

var bobKeys = web3.eth.accounts.create();

console.log(bobKeys);

};

Et voici la sortie que nous obtenons dans la fenêtre de la console après l’exécution de l’extrait précédent.

{

address: ‘0xAff9d328E8181aE831Bc426347949EB7946A88DA’,

privateKey: ‘0x9fb71152b32cb90982f95e2b1bf2a

5b6b2a5385 5eacf59d132a2b7f043cfddf5’,

signTransaction: [Function: signTransaction],

sign: [Function: sign],

encrypt: [Function: encrypt]

}

{

address: ‘0x22013fff98c2909bbFCcdABb411D3715fDB341eA’,

privateKey: ‘0xc6676b7262dab1a3a28a781c77110b63ab8cd5

eae2a5a828ba3b1ad28e9f5a9b’,

signTransaction: [Function: signTransaction],

sign: [Function: sign],

encrypt: [Function: encrypt]

}

Comme vous pouvez le voir, avec les adresses et les clés privées, la sortie pour chaque appel de fonction de création de compte comprend également quelques fonctions.

Pour l’instant, nous allons nous concentrer sur l’adresse et la clé privée des objets retournés. L’adresse est le hachage Keccak-256 de la clé publique ECDSA de la clé privée générée.

Cette combinaison d’adresses et de clés privées représente un compte sur la blockchain Ethereum. Vous pouvez envoyer Ether à l’adresse et vous pouvez passer cet éther en utilisant la clé privée de l’adresse correspondante.

Obtenez l’éther de test dans le compte de l’expéditeur

Maintenant, pour créer une transaction Ethereum qui transfère l’Ether d’un compte à un autre, nous avons d’abord besoin d’un peu d’Éther dans l’un des comptes. Rappelez-vous de la section de programmation Bitcoin que nous avons utilisé des faucet testnet pour obtenir certains Bitcoins test sur l’adresse que nous avons généré.

Nous ferons la même chose pour Ethereum aussi. Rappelez-vous que nous ciblons le réseau de test Ropsten pour Ethereum, donc nous allons rechercher un faucet Ropsten sur Internet. Pour cet exemple, nous avons soumis l’adresse d’Alice que nous avons générée dans l’extrait de code précédent à un faucet du réseau de test Ethereum Ropsten et nous avons reçu trois ethers sur cette adresse.

Après avoir reçu l’ether sur l’adresse d’Alice, vérifions le solde de cette adresse pour confirmer si nous avons vraiment l’éther ou non. Bien que nous puissions vérifier le solde de cette adresse en utilisant l’un des explorateurs Ethereum en ligne, nous allons le faire en utilisant le code. L’extrait de code suivant appelle la fonction getBalance en passant l’adresse d’Alice comme paramètre d’entrée.

var getBalance = function () {

web3.eth.getBalance(‘0xAff9d328E8181aE831Bc426347949

EB7946A88DA’).then(console.log);

};

Et nous obtenons la sortie suivante comme le solde de l’adresse d’Alice. C’est un nombre énorme, mais c’est en fait la valeur de l’équilibre dans wei. Wei est la plus petite unité d’Éther. Un éther est égal à 10^18 wei. Ainsi, la valeur suivante équivaut à trois Éther, qui est ce que nous avons reçu du faucet du réseau de test.

3000000000000000000

Préparer la transaction Ethereum

Maintenant que nous avons un test Ether avec Alice, créons une transaction Ethereum pour envoyer une partie de cet Éther à Bob. Rappelons qu’il n’y a pas d’entrées et de sorties et de requêtes UTXO à faire dans le cas d’Ethereum parce qu’il utilise un système basé sur le compte et les soldes. Donc, tout ce que nous devons faire dans la transaction est de spécifier l’adresse “de” (l’adresse de l’expéditeur), l’adresse “à” (l’adresse du destinataire), et le montant de l’éther à envoyer, entre autres.

Rappelons également que dans le cas d’une transaction Bitcoin, nous n’avons pas à spécifier les frais de transaction ; toutefois, dans le cas d’une transaction Ethereum, nous devons spécifier deux domaines connexes. L’un est la limite de gas et l’autre est le prix du gas. Rappel du chapitre 4, le gas est l’unité des frais de transaction que nous devons payer au réseau Ethereum pour obtenir nos transactions confirmées et ajoutées aux blocs. Le prix du gas est la quantité d’éther (en gwei) que nous voulons payer par unité de gas. Les frais maximaux que nous permettons d’être utilisés pour une transaction sont le produit du gas par le prix du gas.

Ainsi, pour cette transaction par exemple, nous définissons un objet JSON avec les champs suivants. Ici, “de” a l’adresse d’Alice et “à” a l’adresse de Bob, et la valeur est un Ether dans wei. Le prix du gas que nous choisissons est de 20 gwei et la quantité maximale de gas que nous voulons payer pour cette transaction est de 42 000.

Nous avons laissé le champ de données vide. Nous y reviendrons plus tard dans la section des contrats intelligents.

{

from: “0xAff9d328E8181aE831Bc426347949EB7946A88DA”,

gasPrice: “20000000000”,

gas: “42000”,

to: ‘0x22013fff98c2909bbFCcdABb411D3715fDB341eA’,

value: “1000000000000000000”,

data: “”

}

Signature de Transaction

Maintenant que nous avons créé un objet de transaction avec les champs et les valeurs requis, nous devons le signer en utilisant la clé privée du compte qui envoie l’éther. Dans ce cas, l’expéditeur est Alice, donc nous allons utiliser la clé privée d’Alice pour signer la transaction. C’est pour prouver cryptographiquement que c’est en fait Alice qui dépense l’éther dans son compte.

var signTransaction = function () {

var tx = {

from: “0xAff9d328E8181aE831Bc426347949EB7946A88DA”,

gasPrice: “20000000000”,

gas: “42000”,

to: ‘0x22013fff98c2909bbFCcdABb411D3715fDB341eA’,

value: “1000000000000000000”,

data: “”

};

web3.eth.accounts.signTransaction(tx, ‘0x9fb71152b32cb

90982f95e2b1bf2a5b6b2a53855eacf59d132a2b7f043cfddf5’)

.then(function(signedTx){

console.log(signedTx.rawTransaction);

});

};

L’extrait de code précédent appelle la fonction signTransaction avec l’objet transactionnel que nous avons créé dans l’étape précédente et la clé privée d’Alice que nous avons eue lorsque nous avons généré le compte d’Alice. Voici la sortie que nous obtenons lorsque nous lançons l’extrait de code de suivant.

{

messageHash: ‘0x91b345a38dc728dc06a43c49b922a6ac1e0e6d
614c432a6dd37d809290a25aa6b,dans: ‘0x2a’,
r: ‘0x14c20901a060834972a539d7b8ad1f23161 c2144a2b66fbf567e37e963d64537’,
s: ‘0x3d2a0a818633a11832a5c48708a198af909 eaf4884a7856c9ac9ed216d9b029c’,
rawTransaction: ‘0xf86c018504a817c80082a4109422013fff98c
2909bbfccdabb411d3715fdb341ea880de0b6b3a76400
00802aa014c20901a060834972a539d7b8ad1f23161c2144a2b66fbf5
67e37e963d64537a03d2a0a88633a1832a5c48708a198af909ea f4884a7856c9ac9ed216d9b029c’

}

Dans la sortie de la fonction signTransaction nous recevons un objet JSON avec quelques propriétés. La valeur importante pour nous est la valeur rawTransaction. Il s’agit de la représentation de la chaîne hex de la transaction signée. C’est très similaire à la façon dont nous avons créé une chaîne hex de la transaction Bitcoin dans la section Bitcoin.

Envoyer Transaction au réseau Ethereum

La dernière étape consiste à simplement envoyer cette transaction brute signée au nœud public du réseau de test Ethereum, que nous avons mis en tant que fournisseur de notre objet web3.

Le code suivant appelle la fonction sendSignedTransaction pour envoyer la transaction brute au réseau de test Ethereum. Le paramètre d’entrée est la valeur de la chaîne rawTransaction que nous avons obtenu dans l’étape précédente dans le cadre de la signature de la transaction.

web3.eth.sendSignedTransaction(signedTx.rawTransaction).

then(console.log);

Ceci est intéressant parce que la bibliothèque web3 fournit différents niveaux de finalité lors de la collaboration avec les transactions Ethereum, parce qu’une transaction Ethereum passe par plusieurs états après avoir été soumis. Dans cette fonction, l’appel d’envoi d’une transaction au réseau, puis, est frappé lorsque le reçu de transaction est créé, et la transaction est terminée.

Après quelques secondes, lorsque la promesse JavaScript se résout, ce qui suit est ce que nous obtenons comme une sortie.

{

blockHash: ‘0x26f1e1374d11d4524f692cdf1ce3aa6e085dcc1810
84642293429eda3954d30e’,
blockNumber: 2514764,
contractAddress: null,
cumulativeGasUsed: 125030,
from: ‘0xaff9d328e8181ae831bc426347949eb7946a88da’,
gasUsed: 21000,
logs: [],
logsBloom: ‘0x0000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000000000
00000000000000000’,
status: ‘0x1’,
to: ‘0x22013fff98c2909bbfccdabb411d3715fdb341ea’,
transactionHash: ‘0xd3f45394ac038c44c4fe6e0cdb7021fdbd
672eb1abaa93eb6a1828df5edb6253’,
transactionIndex: 3

}

La sortie a beaucoup d’informations, comme nous pouvons le voir. La partie la plus importante est la transactionHash, qui est l’ID de la transaction sur le réseau. Il nous donne également le blockHash, qui est l’ID du bloc dans lequel cette transaction a été incluse. En plus de cela, nous obtenons également des informations sur la quantité de gas a été utilisé pour cette transaction, entre autres détails. Si le gas utilisé est inférieur au gas maximum que nous avons spécifié lors de la création de la transaction, le gas restant est renvoyé à l’adresse de l’expéditeur.

Dans cette section, nous avons envoyé une simple transaction à la blockchain Ethereum en utilisant JavaScript. Mais ce n’est que le début de la programmation d’applications Ethereum. Dans la section suivante, nous examinerons également comment créer et appeler des contrats intelligents de façon programmatique.

Interagir programmatiquement avec Ethereum— Création d’un contrat intelligent

Dans cette section, nous poursuivrons notre exercice de programmation Ethereum, et nous créerons un contrat simple et intelligent sur la blockchain Ethereum en utilisant la même bibliothèque JavaScript web3 et l’API du service Infura.

Aucun tutoriel de programmation informatique débutants est complet sans un programme « Hello World », « la base » me direz vous, le contrat intelligent que nous allons créer sera un contrat simple intelligent retour de la chaîne “Hello World” lorsqu’il est appelé.

Le processus de création de contrats sera un type spécial de transaction envoyée à la blockchain Ethereum, et ces types de transactions sont appelés « transactions de création de contrats ». Ces transactions ne mentionnent pas une adresse ” à ” et le propriétaire du contrat intelligent est l’adresse ” à partir ” mentionnée dans la transaction.

Conditions préalables

Dans cet exercice de code pour créer un contrat intelligent, nous allons continuer avec l’hypothèse que la bibliothèque JavaScript web3 est installé et instantiée dans une application node.js et nous nous sommes inscrits pour le service Infura, tout comme nous l’avons fait dans la section précédente.

Voici les étapes pour créer un contrat intelligent sur Ethereum en utilisant JavaScript.

Programmez le contrat intelligent

Rappel du chapitre 4, les contrats intelligents Ethereum sont rédigés dans le langage de programmation Solidity. Bien que la bibliothèque JavaScript web3 nous aidera à déployer notre contrat sur la blockchain Ethereum, nous devrons tout de même écrire et compiler notre contrat intelligent dans Solidity avant de l’envoyer au réseau Ethereum en utilisant le web3. Donc, nous allons d’abord créer un contrat d’échantillon en utilisant Solidity.

Il existe une variété d’outils disponibles pour coder dans Solidity. La plupart des principaux IDE et éditeurs de code ont des plugins Solidity pour l’édition et la compilation de contrats intelligents. Il y a aussi un éditeur Solidity basé sur le Web appelé Remix. Il est disponible gratuitement à https://remix.ethereum.org/. Remix fournit une interface très simple pour coder et compiler des contrats intelligents dans votre navigateur. Dans cet exercice, nous allons utiliser Remix pour coder et tester notre contrat intelligent, puis nous allons envoyer le même contrat au réseau Ethereum en utilisant la bibliothèque JavaScript web3 et le service API Infura.

L’extrait de code suivant est écrit dans le langage de programmation Solidity et c’est un contrat simple et intelligent qui renvoie la chaîne “Hello World” de sa fonction Hello. Il dispose également d’un constructeur qui définit la valeur du message retourné.

pragma solidity ^0.4.0;

contract HelloWorld {

string message;

function HelloWorld(){

message = “Hello World!”;

}

function Hello() constant returns (string) {

return message;

}

}

Allons à Remix et coller ce code dans la fenêtre de l’éditeur. Les images suivantes (Figures 5-4 et 5-5) montrent à quoi ressemble notre contrat intelligent d’échantillon dans l’éditeur Remix et à quoi ressemble la sortie lorsque nous avons cliqué sur le bouton Create sur le menu du côté droit, sous l’onglet Run. En outre, notez que par défaut, l’éditeur Remix cible un environnement JavaScript VM pour la compilation de contrats intelligents et il utilise un compte de test avec un certain solde ETH, à des fins de test. Lorsque nous cliquons sur le bouton Create, ce contrat est créé à l’aide du compte sélectionné dans l’environnement JavaScript VM.

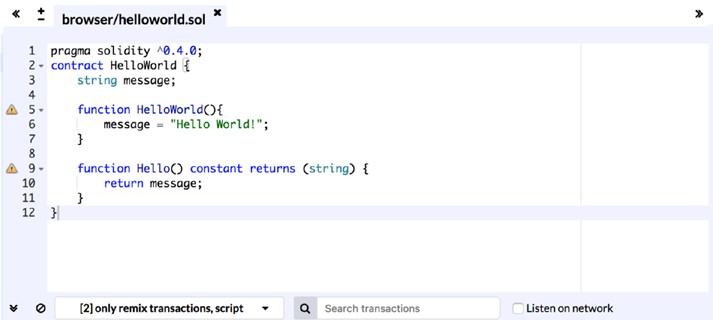
Figure 5-4. Montage de contrats intelligents dans Remix IDE

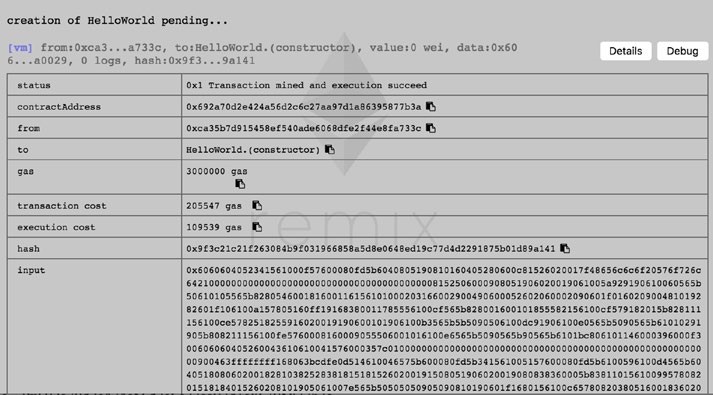
Figure 5-5. Sortie de création de contrat intelligent dans l’IDE Remix

Voici la sortie générée par l’opération de création, il nous montre que le contrat a été créé parce qu’il a une adresse de contrat. La valeur « FROM » est l’adresse de compte qui a été utilisée pour créer le contrat. Il nous montre également le hachage de la transaction de création de contrat.

status 0x1 Transaction mined and execution succeed
contractAddress 0x692a70d2e424a56d2c6c27aa97d1a86395877b3a
from 0xca35b7d915458ef540ade6068dfe2f44e8fa733c
to HelloWorld.(constructor)
gas 3000000 gas
transaction cost 205547 gas
execution cost 109539 gas
hash 0x9f3c21c21f263084b9f031966858a5d8e0648ed19c77d4d2291
875b01d89a141
input 0x6060604052341561000f57600080fd5b6040805190810160405
280600c81526020017f48656c6c6f20576f726c642100000000000000000
000000000000000000000008152506000908051906020019061005a92919
0610060565b50610105565b8280546001816001161561010002031660029
00490600052602060002090601f016020900481019282601f106100a1578
05160ff19168380011785556100cf565b828001600101855582156100cf5
79182015b828111156100ce5782518255916020019190600101906100b35
65b5b5090506100dc91906100e0565b5090565b61010291905b808211156
100fe5760008160009055506001016100e6565b5090565b90565b6101bc8
06101146000396000f300606060405260043610610041576000357c01000
00000000000000000000000000000000000000000000000000000900463f
fffffff168063bcdfe0d514610046575b600080fd5b34156100515760008
0fd5b6100596100d4565b604051808060200182810382528381815181526
0200191508051906020019080838360005b8381101561009957808201518
184015260208101905061007e565b50505050905090810190601f1680156
100c65780820380516001836020036101000a031916815260200191505b5
09250505060405180910390f35b6100dc61017c565b60008054600181600
116156101000203166002900480601f01602080910402602001604051908
101604052809291908181526020018280546001816001161561010002031
66002900480156101725780601f106101475761010080835404028352916
0200191610172565b820191906000526020600020905b815481529060010
19060200180831161015557829003601f168201915b50505050509050905
65b6020604051908101604052806000815250905600a165627a7a7230582
0d6796e48540eced3646ea52c632364666e64094479451066317789a712
aef4da0029
decoded input {}
decoded output –
logs [] value 0 wei

À ce stade, nous avons un simple“Hello World”contrat intelligent prêt, et maintenant la prochaine étape est de ledéployer programmatiquement à la blockchain Ethereum.

Compiler le contrat et obtenir des détails

Voyons d’abord quelques détails sur notre contrat intelligent de Remix, qui sera nécessaire pour déployer le contrat sur le réseau Ethereum en utilisant la bibliothèque web3. Cliquez sur l’onglet Compile dans le menu du côté droit, puis cliquez sur le bouton Détails. Cela apparaît une nouvelle fenêtre enfant avec les détails du contrat intelligent. Ce qui est important pour nous, ce sont les sections ABI et BYTECODE sur la fenêtre popup du détail.

Copions les détails dans la section ABI en utilisant la valeur de copie au bouton de presse-papiers disponible à côté de l’en-tête ABI. Voici la valeur des données ABI pour notre contrat intelligent.

[

{

“constant”: true,

“inputs”: [],

“name”: “Hello”,

“outputs”: [

{

“name”: “”,

“type”: “string”

}

],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

},

{

“inputs”: [],

“payable”: false,

“stateMutability”: “nonpayable”,

“type”: “constructor”

}

]

Il s’agit d’un tableau JSON et si nous le regardons de près, nous voyons qu’il a des objets JSON pour chaque fonction dans notre contrat, y compris son constructeur. Ces objets JSON ont des détails sur une fonction, son entrée et sa sortie. Ce tableau décrit l’interface de contrat intelligente.

Lorsque nous appelons ce contrat intelligent après qu’il soit déployé sur le réseau, nous aurons besoin de cette information pour savoir quelles fonctions le contrat est exposer et ce que nous devons passer comme une entrée à la fonction que nous souhaitons appeler.

Maintenant, nous allons obtenir le détail des données dans la section BYTECODE apparaissant. Voici les données que nous avons copiées pour notre contrat.

{

“linkReferences”: {},
“object”: “6060604052341561000f57600080fd5b6040805190810 160405280600c81526020017f48656c6c6f20576f726c64210000000
00000000000000000000000000000000081525060009080519060200
19061005a929190610060565b50610105565b8280546001816001161
56101000203166002900490600052602060002090601f01602090048
1019282601f106100a157805160ff19168380011785556100cf565b8
28001600101855582156100cf579182015b828111156100ce5782518
255916020019190600101906100b3565b5b5090506100dc91906100e
0565b5090565b61010291905b808211156100fe57600081600090555
06001016100e6565b5090565b90565b6101bc806101146000396000f
300606060405260043610610041576000357c0100000000000000000
000000000000000000000000000000000000000900463ffffffff168 063bcdfe0d514610046575b600080fd5b341561005157600080fd5b6
100596100d4565b60405180806020018281038252838181518152602
00191508051906020019080838360005b83811015610099578082015
18184015260208101905061007e565b50505050905090810190601f1
680156100c65780820380516001836020036101000a0319168152602
00191505b509250505060405180910390f35b6100dc61017c565b600
08054600181600116156101000203166002900480601f01602080910
40260200160405190810160405280929190818152602001828054600
181600116156101000203166002900480156101725780601f1061014
757610100808354040283529160200191610172565b8201919060005
26020600020905b81548152906001019060200180831161015557829
003601f168201915b5050505050905090565b6020604051908101604
052806000815250905600a165627a7a72305820877a5da4f7e05c4ad
9b45dd10fb6c133a523541ed06db6dd31d59b35d51768a30029”,

“opcodes”: “PUSH1 0x60 PUSH1 0x40 MSTORE CALLVALUE
ISZERO PUSH2 0xF JUMPI PUSH1 0x0 DUP1 REVERT JUMPDEST
PUSH1 0x40 DUP1 MLOAD SWAP1 DUP2 ADD PUSH1 0x40 MSTORE
DUP1 PUSH1 0xC DUP2 MSTORE PUSH1 0x20 ADD PUSH32
0x48656C6C6F20576F726C64210000000000000000000000000000000000
000000 DUP2 MSTORE POP PUSH1 0x0 SWAP1 DUP1 MLOAD SWAP1 PUSH1
0x20 ADD SWAP1 PUSH2 0x5A SWAP3 SWAP2 SWAP1 PUSH2 0x60 JUMP
JUMPDEST POP PUSH2 0x105 JUMP JUMPDEST DUP3 DUP1 SLOAD PUSH1
0x1 DUP2 PUSH1 0x1 AND ISZERO PUSH2 0x100 MUL SUB AND PUSH1
0x2 SWAP1 DIV SWAP1 PUSH1 0x0 MSTORE PUSH1 0x20 PUSH1 0x0
KECCAK256 SWAP1 PUSH1 0x1F ADD PUSH1 0x20 SWAP1 DIV DUP2 ADD
SWAP3 DUP3 PUSH1 0x1F LT PUSH2 0xA1 JUMPI DUP1 MLOAD PUSH1 0xFF
NOT AND DUP4 DUP1 ADD OR DUP6 SSTORE PUSH2 0xCF JUMP JUMPDEST
DUP3 DUP1 ADD PUSH1 0x1 ADD DUP6 SSTORE DUP3 ISZERO PUSH2
0xCF JUMPI SWAP2 DUP3 ADD JUMPDEST DUP3 DUP2 GT ISZERO PUSH2
0xCE JUMPI DUP3 MLOAD DUP3 SSTORE SWAP2 PUSH1 0x20 ADD SWAP2
SWAP1 PUSH1 0x1 ADD SWAP1 PUSH2 0xB3 JUMP JUMPDEST JUMPDEST
POP SWAP1 POP PUSH2 0xDC SWAP2 SWAP1 PUSH2 0xE0 JUMP JUMPDEST
POP SWAP1 JUMP JUMPDEST PUSH2 0x102 SWAP2 SWAP1 JUMPDEST DUP1
DUP3 GT ISZERO PUSH2 0xFE JUMPI PUSH1 0x0 DUP2 PUSH1 0x0 SWAP1
SSTORE POP PUSH1 0x1 ADD PUSH2 0xE6 JUMP JUMPDEST POP SWAP1
JUMP JUMPDEST SWAP1 JUMP JUMPDEST PUSH2 0x1BC DUP1 PUSH2
0x114 PUSH1 0x0 CODECOPY PUSH1 0x0 RETURN STOP PUSH1 0x60
PUSH1 0x40 MSTORE PUSH1 0x4 CALLDATASIZE LT PUSH2 0x41 JUMPI
PUSH1 0x0 CALLDATALOAD PUSH29 0x1000000000000000000000000000
00000000000000000000000000000 SWAP1 DIV PUSH4 0xFFFFFFFF AND
DUP1 PUSH4 0xBCDFE0D5 EQ PUSH2 0x46 JUMPI JUMPDEST PUSH1 0x0

DUP1 REVERT JUMPDEST CALLVALUE ISZERO PUSH2 0x51 JUMPI PUSH1
0x0 DUP1 REVERT JUMPDEST PUSH2 0x59 PUSH2 0xD4 JUMP JUMPDEST
PUSH1 0x40 MLOAD DUP1 DUP1 PUSH1 0x20 ADD DUP3 DUP2 SUB DUP3
MSTORE DUP4 DUP2 DUP2 MLOAD DUP2 MSTORE PUSH1 0x20 ADD SWAP2
POP DUP1 MLOAD SWAP1 PUSH1 0x20 ADD SWAP1 DUP1 DUP4 DUP4 PUSH1
0x0 JUMPDEST DUP4 DUP2 LT ISZERO PUSH2 0x99 JUMPI DUP1 DUP3
ADD MLOAD DUP2 DUP5 ADD MSTORE PUSH1 0x20 DUP2 ADD SWAP1 POP
PUSH2 0x7E JUMP JUMPDEST POP POP POP POP SWAP1 POP SWAP1 DUP2
ADD SWAP1 PUSH1 0x1F AND DUP1 ISZERO PUSH2 0xC6 JUMPI DUP1
DUP3 SUB DUP1 MLOAD PUSH1 0x1 DUP4 PUSH1 0x20 SUB PUSH2 0x100
EXP SUB NOT AND DUP2 MSTORE PUSH1 0x20 ADD SWAP2 POP JUMPDEST
POP SWAP3 POP POP POP PUSH1 0x40 MLOAD DUP1 SWAP2 SUB SWAP1
RETURN JUMPDEST PUSH2 0xDC PUSH2 0x17C JUMP JUMPDEST PUSH1 0x0
DUP1 SLOAD PUSH1 0x1 DUP2 PUSH1 0x1 AND ISZERO PUSH2 0x100
MUL SUB AND PUSH1 0x2 SWAP1 DIV DUP1 PUSH1 0x1F ADD PUSH1
0x20 DUP1 SWAP2 DIV MUL PUSH1 0x20 ADD PUSH1 0x40 MLOAD SWAP1
DUP2 ADD PUSH1 0x40 MSTORE DUP1 SWAP3 SWAP2 SWAP1 DUP2 DUP2
MSTORE PUSH1 0x20 ADD DUP3 DUP1 SLOAD PUSH1 0x1 DUP2 PUSH1 0x1
AND ISZERO PUSH2 0x100 MUL SUB AND PUSH1 0x2 SWAP1 DIV DUP1
ISZERO PUSH2 0x172 JUMPI DUP1 PUSH1 0x1F LT PUSH2 0x147 JUMPI PUSH2 0x100 DUP1 DUP4 SLOAD DIV MUL DUP4 MSTORE SWAP2 PUSH1
0x20 ADD SWAP2 PUSH2 0x172 JUMP JUMPDEST DUP3 ADD SWAP2 SWAP1
PUSH1 0x0 MSTORE PUSH1 0x20 PUSH1 0x0 KECCAK256 SWAP1 JUMPDEST
DUP2 SLOAD DUP2 MSTORE SWAP1 PUSH1 0x1 ADD SWAP1 PUSH1 0x20
ADD DUP1 DUP4 GT PUSH2 0x155 JUMPI DUP3 SWAP1 SUB PUSH1 0x1F
AND DUP3 ADD SWAP2 JUMPDEST POP POP POP POP POP SWAP1 POP
SWAP1 JUMP JUMPDEST PUSH1 0x20 PUSH1 0x40 MLOAD SWAP1 DUP2
ADD PUSH1 0x40 MSTORE DUP1 PUSH1 0x0 DUP2 MSTORE POP SWAP1
JUMP STOP LOG1 PUSH6 0x627A7A723058 KECCAK256 DUP8 PUSH27
0x5DA4F7E05C4AD9B45DD10FB6C133A523541ED0
6DB6DD31D59B35D5 OR PUSH9 0xA30029000000000000 “,
“sourceMap”: “24:199:0:-;;;75:62;;;;;;;;106:24;;;;;;;;;;;; ;;;;;;:7;:24;;;;;;;;;;;;:::i;:::-;;24:199;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;:::i;:::-;;;:::o;:::-;;;;;;;;;;;;;;;;
;;;;;;;;;;;:::o;:::-;;;;;;;”
}

Comme nous pouvons le voir, les données de la section BYTECODE sont un des objets JSON. Il s’agit essentiellement de la sortie de la compilation du contrat intelligent. Remix a compilé notre contrat intelligent à l’aide du compilateur Solidity et, par conséquent, nous avons obtenu le code octet de solidité. Maintenant, examinez de près ce JSON et regardez la propriété “objet” et sa valeur. Il s’agit d’une chaîne hexagonale qui contient le code octet pour notre contrat intelligent, et nous l’enverrons dans la transaction de création de contrat dans le domaine des données, le même champ de données que nous avons laissé vide dans l’exemple précédent Ethereum transaction entre Alice et Bob.

Maintenant, nous avons tous les détails pour notre contrat intelligent et nous sommes prêts à l’envoyer au réseau Ethereum.

Contrat de déploiement sur le réseau Ethereum

Maintenant que nous avons notre contrat intelligent, nous devons préparer une transaction qui peut déployer ce contrat sur la blockchain Ethereum. Cette préparation de transaction sera très similaire à la transaction que nous avons préparée dans la section précédente, mais elle aura quelques propriétés de plus qui sont nécessaires pour créer des contrats.

Tout d’abord, nous devons créer un objet de la classe web3.eth.Contract, qui peut représenter notre contrat. L’extrait de code suivant crée une instance pour la dite classe avec un tableau JSON comme paramètre d’entrée. C’est le même tableau JSON que nous avons copié à partir de la section ABI de la fenêtre popup Remix, montrant les détails de notre contrat intelligent.

var helloworldContract = new web3.eth.Contract([{

“constant”: true,

“inputs”: [],

“name”: “Hello”,

“outputs”: [{

“name”: “”,

“type”: “string”

}],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

}, {

“inputs”: [],

“payable”: false,

“stateMutability”: “nonpayable”,

“type”: “constructor”

}]);

Maintenant, nous devons envoyer ce contrat au réseau Ethereum en utilisant la méthode Contract.deploy de la bibliothèque web3. L’extrait de code suivant montre comment le faire.

helloworldContract

.deploy({

data: ‘0x6060604052341561000f57600080fd5b604080519081 0160405280600c81526020202020200017f48886020202020202020017f48860202020200017f4800000000000000000000000000000000000008152506000908051906020019061005a929190610060565b5061010555555b828054600181600116156101000203166002900490600052602060002090601f016020900481019282601f106100a157805160ff19168380011785556100cf565b828001600101855582156779182015b82811115610005572518825252020202020019190200101010100090506100dc9190610000565b5090565b61010105b808211 156100fe5760000816000090555060001010100e6555065b6101bc8061011460003960000f300606060604052600043610610041576000357c0100000000000000000000000000000000000000000000000000000000000000000900463ffffffff168063bcdfe0d514610046575b600080fd5b341561005157600080fd5b6100596100d4565b6040518080602001828103825283818151815260200191508051906020019080838360005b83811010156100957808201518184015260208101905061007e565b50505050905090810190601f1680156100c65780820380516001836020036100000031916815260200191505b509250505060405180910390f35b6100dc61017c565b60008054600181600116156100020316002900480601f016020809104026020016040519081016040528092999190818152602020018280 5460018181601616160000203160020 10610147776101008083540402835221602019161010172565b82 01919060000052020202002002002005b8154831161015557829003601f168201915b5050505090509090565b6020604051908101604052806000815250905600a165627a7a72305820877a5da4f7e05c4ad9b45dd10fb6c133a523541ed06db6dd31 d59b35d51768a30029’

})

.send({

from: ‘0xAff9d328E8181aE831Bc426347949EB7946A88DA’,
gas: 4700000,
gasPrice: ‘20000000000000’

},

function(error, transactionHash){

console.log(error);
console.log(transactionHash);

})

.then(function(contract){

console.log(contract);

});

La valeur des données de champ à l’intérieur de l’objet de paramètre de fonction de déploiement est la même valeur que nous avons reçue dans le champ d’objet des détails BYTECODE dans l’étape précédente.

La chaîne “0x” est ajoutée à cette valeur au début. Ainsi, les données transmises dans la fonction de déploiement est ‘0x’ + byte code du contrat.

À l’intérieur de la fonction d’envoi après le déploiement, nous avons ajouté l’adresse “de” qui sera le propriétaire du contrat et les détails des frais de transaction de la limite de gas et le prix du gas. Enfin, lorsque l’appel est terminé, l’objet du contrat est retourné. Cet objet du contrat aura les détails du contrat ainsi que l’adresse du contrat, qui peut être utilisé pour appeler la fonction sur le contrat.

Une autre façon d’envoyer le contrat au réseau serait d’envelopper le contrat à l’intérieur d’une transaction et de l’envoyer directement. L’extrait de code suivant crée un objet de transaction avec des données comme BYTECODE du contrat, le signe en utilisant la clé privée de l’adresse dans le champ “de” et l’envoie ensuite à la blockchain Ethereum.

Notez que nous n’avons pas attribué d’adresse « à» dans cet objet transactionnel, car l’adresse du contrat est inconnue avant le déploiement du contrat.

var tx = {

from: “0x22013fff98c2909bbFCcdABb411D3715fDB341eA”,
gasPrice: “20000000000”,
gas: “4900000”,
data: “0x6060604052341561000f57600080fd5b604080519081
0160405280600c81526020017f48656c6c6f20576f726c642100000000000000000000000000000000000000008152506000908051906020019061005a929190610060565b50610105565b828054600181600116156101000203166002900490600052602060002090601f016020900481019282601f106100a157805160ff19168380011785556100cf565b828001600101855582156100cf579182015b828111156100ce5782518255916020019190600101906100b3565b5b5090506100dc91906100e0565b5090565b61010291905b808211156100fe5760008160009055506001016100e6565b5090565b90565b6101bc806101146000396000f300606060405260043610610041576000357c0100000000000000000000000000000000000000000000000000000000900463ffffffff168063bcdfe0d514610046575b600080fd5b341561005157600080fd5b6100596100d4565b6040518080602001828103825283818151815260200191508051906020019080838360005b8381101561009957808201518184015260208101905061007e565b50505050905090810190601f1680156100c65780820380516001836020036101000a031916815260200191505b509250505060405180910390f35b6100dc61017c565b60008054600181600116156101000203166002900480601f0160208091040260200160405190810160405280929190818152602001828054600181600116156101000203166002900480156101725780601f1061014757610100808354040283529160200191610172565b820191906000526020600020905b81548152906001019060200180831161015557829003601f168201915b5050505050905090565b6020604051908101604052806000815250905600a165627a7a72305820877a5da4f7e05c4ad9b45dd10fb6c133a523541ed06db6dd31d59b35d51768a30029”

};

web3.eth.accounts.signTransaction(tx, ‘0xc6676b7262dab1a3
a28a781c77110b63ab8cd5eae2a5a828ba3b1ad28e9f5a9b’)

.then(function (signedTx) {

web3.eth.sendSignedTransaction(signedTx.rawTransaction)

.then(console.log);

});

Lorsque nous exécutons cet extrait de code, nous obtenons la sortie suivante, qui est la réception de cette transaction.

{

blockHash: ‘0xaba93b4561fc35e062a1ad72460e0b677603331bbee
3379ce6c74fa5cf505d82’,

blockNumber: 2539889,

contractAddress: ‘0xd5a2d13723A34522EF79bE0f1E7806E86a45
78E9’,

cumulativeGasUsed: 205547,

from: ‘0x22013fff98c2909bbfccdabb411d3715fdb341ea’,

gasUsed: 205547,

logs: [],

logsBloom: ‘0x0000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000’,

status: ‘0x1’,

to: null,

transactionHash: ‘0xc333cbc5fc93b52871689aab22c48b910cb19
2b4875bea69212363030d36565a’,

transactionIndex: 0

}

Notez les propriétés de l’objet de réception de transaction. Il a une valeur attribuée à la propriété contractAddress, tandis que la valeur de la propriété “à” est nulle. Cela signifie qu’il s’agissait d’une transaction de création de contrat qui a été exploitée avec succès sur le réseau et le contrat créé dans le cadre de cette transaction est déployé à l’adresse ‘0xd5a2d13723A34522EF79bE0f1E7806E86a4578E9‘.

Nous avons réussi à créer un contrat intelligent Ethereum programmatiquement.

Interagir programmatiquement avec Ethereum — Exécution de fonctions contractuelles intelligentes

Maintenant que nous avons déployé notre contrat intelligent sur le réseau Ethereum, nous pouvons appeler ses fonctions membres. Voici les étapes pour appeler un contrat intelligent Ethereum programmatiquement.

Obtenir la référence au contrat intelligent

Pour exécuter une fonction du contrat intelligent, nous devons d’abord créer une instance de la classe web3.eth.Contract avec l’ABI et l’adresse de notre contrat déployé. L’extrait de code suivant montre comment le faire.

var helloworldContract = new web3.eth.Contract([{

“constant”: true,
“inputs”: [],
“name”: “Hello”,
“outputs”: [{

“name”: “”,
“type”: “string”

}],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

}, {

“inputs”: [],
“payable”: false,
“stateMutability”: “nonpayable”,
“type”: “constructor”

}], ‘0xd5a2d13723A34522EF79bE0f1E7806E86a4578E9’);

Dans l’extrait de code d’écaillage, nous avons créé une instance de la classe web3.eth.Contract en passant l’ABI du contrat que nous avons créé dans la section précédente, et nous avons également passé l’adresse du contrat que nous avons reçu après le déploiement du contrat.

Cet objet peut maintenant être utilisé pour appeler des fonctions sur notre contrat.

Exécuter la fonction de contrat intelligente

Rappelons que nous n’avons qu’une seule fonction publique dans notre contrat. Cette méthode est nommée Bonjour et il retourne la chaîne “ Hello World! “ lorsqu’il est exécuté. Pour exécuter cette méthode, nous l’appellerons en utilisant la classe contract.methods dans la bibliothèque web3. L’extrait de code suivant le montre.

helloworldContract.methods.Hello().send({
from: ‘0xF68b93AE6120aF1e2311b30055976d62D7dBf531’
}).then(console.log);

Dans l’extrait de code précèdent, nous avons ajouté une valeur à l’adresse “de” dans la fonction d’envoi, et cette adresse sera utilisée pour envoyer la transaction qui à son tour exécutera la fonction Hello sur notre contrat intelligent. Le code complet pour appeler un contrat intelligent est dans l’extrait de code suivant.

var callContract = function () {

var helloworldContract = new web3.eth.Contract([{

“constant”: true,
“inputs”: [],
“name”: “Hello”,
“outputs”: [{

“name”: “”,
“type”: “string”

}],

“payable”: false,
“stateMutability”: “view”,
“type”: “function”

}, {

“inputs”: [],
“payable”: false,
“stateMutability”: “nonpayable”,
“type”: “constructor”

}], ‘0xd5a2d13723A34522EF79bE0f1E7806E86a4578E9’);

helloworldContract.methods.Hello().send({

from: ‘0xF68b93AE6120aF1e2311b30055976d62D7dBf531’

}).then(console.log);

};

Une autre façon d’exécuter cette fonction de contrat sera en envoyant une transaction brute en la signant. Il est similaire à la façon dont nous avons envoyé une transaction Ethereum brute pour envoyer Ether et de créer un contrat dans les sections précédentes. Dans ce cas, tout ce que nous avons à faire est de fournir l’adresse du contrat dans le champ “à” de l’objet transactionnel et la valeur ABI codée de l’appel de fonction dans le champ de données.

L’extrait de code suivant crée d’abord un objet contractuel, puis obtient la valeur ABI codée de la fonction de contrat intelligente à appeler. Il crée ensuite un objet de transaction basé sur ces valeurs, puis le signe et l’envoie au réseau. Notez que nous avons utilisé la fonction encodeABI sur la fonction contrat pour obtenir la valeur de charge utile des données pour la transaction. C’est l’entrée pour le contrat intelligent.

var callContract = function () {

var helloworldContract = new web3.eth.Contract([{

“constant”: true,
“inputs”: [],
“name”: “Hello”,
“outputs”: [{

“name”: “”,

“type”: “string”

}],

“payable”: false,
“stateMutability”: “view”,
“type”: “function”

}, {

“inputs”: [],

“payable”: false,

“stateMutability”: “nonpayable”,

“type”: “constructor”

}], ‘0xd5a2d13723A34522EF79bE0f1E7806E86a4578E9’);

var payload = helloworldContract.methods.Hello().encodeABI();

var tx = {

from: “0xF68b93AE6120aF1e2311b30055976d62D7dBf531”,
gasPrice: “20000000000”,
gas: “4700000”,
data: payload

};

web3.eth.accounts.signTransaction(tx, ‘0xc6676b7262dab1a3
a28a781c77110b63ab8cd5eae2a5a828ba3b1ad28e9f5a9b’)

.then(function (signedTx) {

web3.eth.sendSignedTransaction(signedTx.raw
Transaction)
.then(console.log);

});

};

Lorsque vous utilisez un nœud hébergé par le public pour l’éthereum, nous devrions utiliser la méthode de transaction brute pour créer et exécuter des contrats intelligents parce que le sous-module web3.eth.Contract de la bibliothèque utilise soit un compte déverrouillé ou par défaut associé au nœud ethereum fournisseur, mais cela n’est pas pris en charge par les nœuds publics (au moment de la rédaction).

Concepts Blockchain revisités

Dans les sections précédentes, nous avons envoyé des transactions programmatiques aux blockchains Bitcoin et Ethereum à l’aide de JavaScript. Voici quelques-uns des concepts communs que nous pouvons maintenant revoir, en examinant le processus d’artisanat des transactions en utilisant le code.

• Transactions : En regardant le code que nous avons écrit et la sortie que nous avons obtenu pour l’envoi de transactions à Ethereum et Bitcoin, nous pouvons maintenant dire que les transactions blockchain sont les opérations initiées par un propriétaire de compte, qui, si elles sont complétées avec succès, mettront à jour l’état de la blockchain. Par exemple, dans nos transactions entre Alice et Bob, nous avons vu que la propriété d’une certaine quantité de Bitcoins et Ether a changé d’Alice à Bob et vice versa, et ce changement de propriété a été enregistré dans la blockchain, ce qui l’amène dans un nouvel état. Dans le cas d’Ethereum, les transactions vont plus loin dans la création et l’exécution des contrats et ces transactions mettent également à jour l’état de la blockchain. Nous avons créé une transaction qui, à son tour, a déployé un contrat intelligent sur la blockchain Ethereum. L’état de la blockchain a été mis à jour parce que maintenant nous avons un nouveau compte de contrat créé dans la blockchain.
• Entrées, sorties, comptes et soldes : Nous avons également vu comment Bitcoin et Ethereum sont différents les uns des autres en termes de gestion de l’État. Alors que Bitcoin utilise le modèle UTXO, Ethereum utilise le modèle des comptes et des soldes. Cependant, l’idée sous-jacente est à la fois les blockchains enregistrant la propriété des actifs, et les transactions qui sont utilisées pour changer la propriété de ces actifs.
• Frais de transaction : Pour chaque transaction que nous faisons sur les réseaux publics de blockchain, nous devons payer des frais de transaction pour que nos transactions soient confirmées par les mineurs. En Bitcoin, cela est automatiquement calculé, pour Ethereum nous devons mentionner les frais maximums que nous sommes prêts à payer en termes du prix du gas et la limite de gas.
• Signature : Dans les deux cas, nous avons également vu qu’après avoir créé un objet transactionnel avec les valeurs requises, nous l’avons signé à l’aide de la clé publique de l’expéditeur. La signature cryptographique est un moyen de prouver la propriété des actifs. Si la signature est incorrecte, la transaction devient invalide.
• Diffusion transactionnelle : Après avoir créé et signé les transactions, nous les avons envoyées aux nœuds blockchain. Bien que nous envoyions nos exemples de transactions aux nœuds de réseau de test Bitcoin et Ethereum hébergés publiquement, nous sommes libres d’envoyer nos transactions à plusieurs nœuds si nous ne faisons pas confiance à tous pour traiter nos transactions. C’est ce qu’on appelle la diffusion transactionnelle.

Pour résumer, lorsque nous interagissons avec les blockchains, si nous avons l’intention de mettre à jour l’état de la blockchain, nous soumettons des transactions signées ; et pour obtenir ces transactions confirmées, nous devons payer des frais au réseau.

Blockchains publiques contre privées

Sur la base du contrôle d’accès, les blockchains peuvent être classées comme publiques et privées. Les blockchains publiques sont également appelées blockchain sans autorisation et les blockchains privées sont également appelées blockchains autorisées. La principale différence entre les deux est le contrôle d’accès. Les blockchains publiques ou sans autorisation ne limitent pas l’ajout de nouveaux nœuds au réseau et n’importe qui peut rejoindre le réseau. Les blockchains privées ont un nombre limité de nœuds dans le réseau et tout le monde ne peut pas rejoindre le réseau. Des exemples de blockchains publiques sont Bitcoin et Ethereum principaux filets. Un exemple de blockchain privée peut être un réseau de quelques nœuds Ethereum connectés les uns aux autres mais non connectés au réseau principal. Ces nœuds seraient collectivement appelés blockchain privée.

Les blockchains privées sont généralement utilisées par les entreprises pour échanger des données entre elles et leurs partenaires et/ou entre leurs sous-organisations.

Lorsque nous développons des applications pour les blockchains, le type de blockchain, public ou privé, fait une différence parce que les règles d’interaction avec la blockchain peuvent ou ne peuvent pas être les mêmes. C’est ce qu’on appelle la gouvernance de la blockchain. Les blockchains publiques ont un ensemble de règles prédéfinies et les règles privées peuvent avoir un ensemble différent de règles par blockchain. Une blockchain privée pour une chaîne d’approvisionnement peut avoir des règles de gouvernance différentes, tandis qu’une blockchain privée pour la gouvernance des protocoles peut avoir des règles différentes. Par exemple, le jeton, le prix du gas, les frais de transaction, les points de terminaison, etc. peuvent ou non être les mêmes dans le registre Ethereum privé susmentionné et le net principal Ethereum. Cela peut également avoir un impact sur nos applications.

Dans nos échantillons de code, nous nous sommes principalement concentrés sur les réseaux de test publics de Bitcoin et Ethereum. Bien que les concepts de base d’interagir avec les déploiements privés de ces blockchains seront toujours les mêmes, il y aura des différences dans la façon dont nous configurons notre code pour pointer vers les réseaux privés.

Architecture d’application décentralisée

En général, les applications décentralisées sont destinées à interagir directement avec les nœuds blockchain sans avoir besoin de composants centralisés entrant dans l’image. Cependant, dans les scénarios pratiques, avec les intégrations de systèmes hérités et les fonctionnalités limitées et la mise à l’échelle des réseaux blockchain actuels, nous devons parfois faire des choix entre la décentralisation complète et l’évolutivité lors de la conception de nos DApps.

Noeuds publics contre nœuds auto-hébergés

Les Blockchains sont des réseaux décentralisés de nœuds. Tous les nœuds ont la même copie de données et ils sont toujours d’accord sur l’état des données. Lorsque nous développons des applications pour les blockchains, nous pouvons faire parler notre application à l’un des nœuds du réseau cible. Il peut y avoir principalement deux configurations pour cela:

• Application et nœud s’exécutent tous les deux localement : l’application et le nœud s’exécutent tous les deux sur la machine locale. Cela signifie que nous aurons besoin de nos utilisateurs d’applications pour exécuter un nœud blockchain local et pointer l’application pour se connecter avec elle. Ce modèle serait un modèle purement décentralisé d’exécution d’une application. Un exemple de ce modèle est le navigateur Mist basé sur Ethereum, qui utilise un nœud geth local.

La figure 5-6 montre cette configuration.

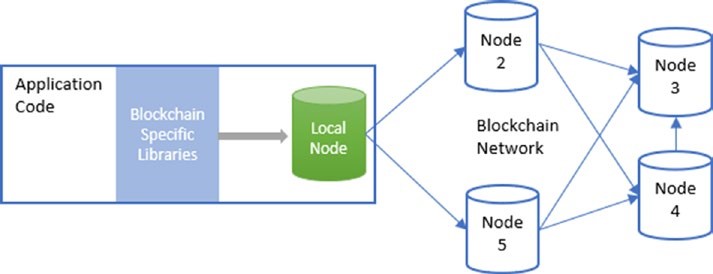
Figure 5-6. DApp connecté au nœud local

• Noeud public : L’application parle à un nœud public hébergé par un tiers. De cette façon, nos utilisateurs n’ont pas à héberger un nœud local. Cette approche présente plusieurs avantages et inconvénients. Bien que les utilisateurs n’aient pas à payer pour l’électricité et le stockage pour l’exécution d’un nœud local, ils ont besoin de faire confiance à un tiers pour diffuser leurs transactions à la blockchain. Le métamasque de plugin du navigateur Ethereum utilise ce modèle et se connecte avec les nœuds Ethereum hébergés par le public.

La figure 5-7 montre cette configuration.

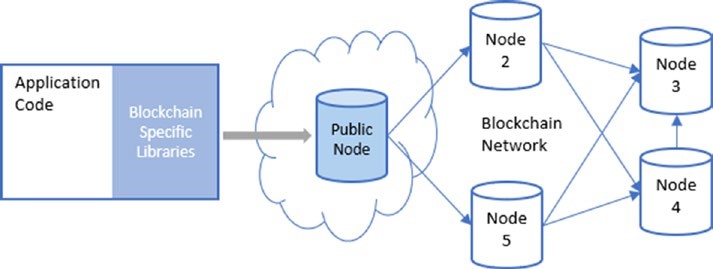
Figure 5-7. DApp connecté au nœud public

Applications et serveurs décentralisés

En dehors des scénarios mentionnés précédemment, il peut y avoir d’autres configurations, en fonction des cas d’utilisations spécifiques et des exigences. Il y a beaucoup de scénarios quand un serveur est nécessaire entre une application et la blockchain. Par exemple : lorsque vous devez maintenir un cache de l’état blockchain pour des requêtes plus rapides ; lorsque l’application a besoin d’envoyer des notifications (emails, push, SMS, etc.) aux utilisateurs en fonction des mises à jour de l’état sur la blockchain ; et lorsque plusieurs registres sont impliqués, et vous devez exécuter une logique back-end pour transformer les données entre les registres.

Imaginez l’infrastructure utilisée par certains des grands échanges de crypto-monnaie où nous obtenons tous les services comme l’authentification à deux facteurs, les notifications et les passerelles de paiement, entre autres choses, et aucun de ces services sont disponibles directement dans l’une des blockchains. Dans un sens plus large, les blockchains s’assurent simplement de garder la couche de données inviolable et vérifiable.

Résumé

Dans ce chapitre, nous avons appris sur le développement d’applications décentralisées avec quelques exercices de code sur l’interaction programmatique avec les blockchains Bitcoin et Ethereum. Nous avons également examiné quelques-uns des modèles d’architecture DApp et comment ils diffèrent en fonction des cas d’utilisation.

Dans le prochain chapitre, nous allons mettre en place un réseau privé Ethereum, puis nous allons développer un DApp à part entière interagissant avec ce réseau privé, qui utilisera également des contrats intelligents pour la logique d’affaires.

CHAPITRE 6 : Développement d’applications Blockchain

Dans le chapitre précédent, nous avons appris à interagir programmatiquement avec les blockchains Bitcoin et Ethereum à l’aide de JavaScript. Nous avons également abordé la façon de créer et de déployer des contrats intelligents Ethereum. Dans ce chapitre, nous allons maintenant notre programmation d’applications blockchain au niveau supérieur en apprenant à développer et à déployer un DApp basé sur la blockchain Ethereum. Dans le cadre de la création de cette DApp, nous allons mettre en place un réseau privé Ethereum et ensuite nous allons utiliser ce réseau comme la blockchain sous-jacente à notre DApp. Ce DApp aura sa logique d’affaires dans un contrat intelligent Ethereum, et cette logique sera exécutée à l’aide d’une application web se connectant au réseau privé Ethereum. De cette façon, nous avons l’intention de couvrir tous les aspects du développement d’applications Ethereum, de la mise en place de nœuds et de réseaux, à la création et au déploiement d’un contrat intelligent, à l’exécution de fonctions contractuelles intelligentes à l’aide d’applications client.

Le DApp

Avant de se mettre au développement de la DApp, nous devons définir le cas d’utilisation pour le DApp. Nous devons également définir les différents composants qui feront partie de notre DApp. Alors, faisons-le d’abord.

Le cas d’utilisation de notre DApp est une application de sondage qui peut permettre aux électeurs de voter sur un sondage publié dans le domaine public. Voter à l’aide d’un système centralisé n’est pas très fiable, car il expose un seul point de corruption et d’échec des données. Ainsi, l’objectif de notre DApp est de permettre des sondages décentralisés. De cette façon, chaque électeur est en contrôle de son vote et chaque vote est traité sur chaque nœud de la blockchain de sorte qu’il n’y a aucun moyen de falsifier les données de vote. Bien que cela puisse être facilement fait en utilisant la blockchain ethereum publique, pour rendre notre exercice intéressant, nous allons déployer notre sondage DApp sur un réseau privé Ethereum, et pour cela nous allons mettre en place le réseau privé aussi. Allons-y.

La première étape consistera à mettre en place un réseau privé Ethereum. Ensuite, pour l’hébergement de la logique métier et les résultats du sondage, nous allons créer un contrat intelligent qui sera déployé sur ce réseau privé Ethereum. Pour interagir avec ce contrat intelligent, nous allons créer une application web front-end en utilisant la bibliothèque web3.

Selon le plan qui vient d’être décrit, notre exercice de développement DApp aura les étapes suivantes:

• Mise en place d’un réseau ethereum privé
• Création d’un contrat intelligent pour la fonctionnalité de sondage
• Déploiement du contrat intelligent sur le réseau privé
• Création d’une application web frontale pour interagir avec le contrat intelligent

Dans les sections suivantes, nous examinerons, en détail, chacune des étapes mentionnées.

Nous pouvons également utiliser le réseau public ethereum pour ce développement dapp. Nous pouvons également utiliser plusieurs outils comme métamasque et le framework Truffle pour accélérer le développement d’un DApp ethereum. ces outils, avec divers autres, nous permettent de gérer notre code et les déploiements d’une meilleure manière.

Le lecteur est encouragé à explorer ces outils et d’autres pour essayer de trouver la meilleure combinaison pour créer un environnement confortable et productif.

Mise en place d’un réseau ethereum privé

Pour mettre en place un réseau ethereum privé, nous aurons besoin de l’un des nombreux clients Ethereum disponibles. En termes simples, un client Ethereum est une application qui implémente le protocole blockchain Ethereum. Il y a beaucoup de clients d’Ethereum disponibles sur l’Internet aujourd’hui ; l’un des plus populaires est go-ethereum, également connu sous le nom geth. Nous allons utiliser geth pour notre réseau privé mis en place. Pour cet exercice, nous utilisons une machine virtuelle exécutant Ubuntu Linux version 16.04.

Installer go-ethereum (geth)

La première étape est d’installer geth sur notre machine locale. Pour installer geth, nous obtiendrons l’installateur exécutable geth de la source officielle https://geth. ethereum.org/downloads/. Cette page de téléchargement sur le site officiel geth répertorie les paquets d’installateurs pour toutes les grandes plates-formes (Windows, macOS, Linux).

Téléchargez le package d’installateur pour votre plate-forme et installez geth sur votre machine locale. Vous pouvez également choisir d’installer geth sur un serveur /cloudhosted) distant si vous ne voulez pas l’installer sur votre machine locale.

Une fois que geth est installé avec succès sur votre machine locale, vous pouvez vérifier l’installation en exécutant la commande suivante dans votre terminal / invite de commande.

version geth

Selon votre système d’exploitation de plate-forme et la version geth que vous avez installé, cette commande doit donner une sortie similaire à la suivante:

Geth Geth

Version: 1.7.3-stable

Git Commit: 4bb3c89d44e372e6a9ab85a8be0c9345265c763a

Architecture: amd64

Versions du protocole: [63 62]

Id réseau: 1

Aller Version: go1.9

Système d’exploitation: linux

GOPATHMD

GOROOTMD/usr/lib/go-1,9

Créer geth Data Directory

Par défaut, geth aura son répertoire de travail, mais nous allons en créer un personnalisé afin que nous puissions le suivre facilement. Il suffit de créer un répertoire et de garder le chemin de ce répertoire à portée de main.

mkdir mygeth

Créer un compte geth

La première chose dont nous avons besoin est un compte Ethereum qui peut contenir Ether. Nous aurons besoin de ce compte pour créer nos contrats intelligents et les transactions plus tard dans le développement DApp. Nous pouvons créer un nouveau compte en utilisant les commandes.

sudo geth account new –datadir <path to the data directory we

created in the previous step>

sudo geth account new –datadir /mygeth

Nous utilisons sudo pour éviter tout problème d’autorisation.

Lorsque vous exécutez cette commande, l’invité demandera une phrase de passage pour verrouiller ce compte. Entrez et confirmez la phrase de passage, puis votre compte geth sera créé. Assurez-vous de vous souvenir de la phrase de passage que vous avez saisie; il sera nécessaire de déverrouiller le compte plus tard pour signer des transactions. L’adresse de ce compte sera affichée à l’écran. Pour nous, l’adresse du compte généré est baf735f889d603f0ec6b1030c91d9033e60525c3. La capture d’écran suivante (figure 6-1) montre ce processus.

Figure 6-1. Configuration du compte Ethereum avec geth

Notez que nous avons passé le répertoire de données comme paramètre pour la commande de compte de création.

Il s’agit de s’assurer que le fichier contenant les détails du compte est créé à l’intérieur de notre répertoire de données afin qu’il soit facile d’accéder au compte à partir du contexte de ce répertoire.

Si nous ne passons pas le paramètre d’annuaire de données aux commandes geth, alors il prendra automatiquement l’emplacement par défaut de l’annuaire de données (qui peut être différent selon la plate-forme).

Créer le fichier de configuration genesis.json

Après l’installation de geth et la création d’un nouveau compte, l’étape suivante consiste à définir la configuration de genèse de notre réseau privé. Comme nous l’avons vu dans les chapitres précédents, les blockchains ont un bloc de genèse qui agit comme point de départ de la blockchain, et toutes les transactions et les blocs sont validés par rapport au bloc de genèse.

Pour notre réseau privé, nous aurons un bloc de genèse personnalisé et donc une configuration de genèse personnalisée. Cette configuration définit certaines valeurs clés pour la blockchain comme le niveau de difficulté, la limite de gas pour les blocs, etc.

La configuration de genèse pour Ethereum a le format suivant comme un objet JSON. Chacune des touches de cet objet est une valeur de configuration qui anime le réseau.

{

“config”: {

“chainId”: 3792,

“homesteadBlock”: 0,

“eip155Block”: 0,

“eip158Block”: 0

},

“difficulty”: “2000”,

“gasLimit”: “2100000”,

“alloc”: {

“baf735f889d603f0ec6b1030c91d9033e60525c3”:

{ “balance”: “9000000000000000000” }

}

}

L’objet JSON est principalement constitué d’une section config ayant des valeurs spécifiques aux numéros de chaîne et de bloc liés à certaines des fourchettes qui ont eu lieu. Le paramètre important à noter ici est le chainId, qui représente l’identifiant de la blockchain et aide à prévenir les attaques de relecture. Pour notre chaîne privée, nous avons opté pour un chainID aléatoire 3792. Vous pouvez choisir n’importe quel nombre ici différent des nombres utilisés par le main net (1) et les test nets (2, 3, et 4).

Le prochain paramètre important est la difficulté. Cette valeur définit à quel point il sera difficile d’exploiter un nouveau bloc. Cette valeur est beaucoup plus élevée dans le réseau principal Ethereum, mais pour les réseaux privés, nous pouvons choisir une valeur relativement plus petite.

Ensuite, il y a le gasLimit. Il s’agit de la limite totale de gas pour un bloc et pas d’une transaction. Une valeur plus élevée signifie généralement plus de transactions dans chaque bloc.

Enfin, nous avons la section alloc. En utilisant cette configuration, nous pouvons préfinancer les comptes Ethereum avec la valeur en wei. Comme nous pouvons le voir, nous avons financé le même compte Ethereum que nous avons créé dans la dernière étape, avec 9 éther.

Exécuter le premier nœud du réseau privé

Pour exécuter le premier nœud de la blockchain privée, nous allons d’abord copier le JSON de l’étape précédente et l’enregistrer comme un fichier nommé genesis.json. Pour plus de simplicité, nous enregistrons ce fichier dans le même répertoire que nous utilisons comme répertoire de données pour geth.

Tout d’abord, nous avons besoin d’initiaslier geth avec le genesis.json. Cette initialisation est nécessaire pour définir la configuration de genèse personnalisée pour notre réseau privé. CD à l’annuaire où nous avons enregistré le fichier genesis.json est

cd mygeth

La commande suivante va initialiser geth avec la configuration personnalisée que nous avons définie.

sudo geth –datadir “/mygeth” init genesis.json

geth confirmera la configuration de genèse personnalisée avec la sortie dans la capture d’écran suivante (figure 6-2).

Figure 6-2. Initialiser geth avec la configuration dans genesis.json

Ensuite, nous devons exécuter geth en utilisant la commande suivante et les paramètres. Nous examinerons chacun de ces paramètres en détail.

sudo geth –datadir “/mygeth” –networkid 8956 –ipcdisable –port 30307 –rpc –rpcapi “eth,web3,personal,net,miner,admin, debug” –rpcport 8507 –mine –minerthreads=1 –etherbase=0xbaf 735f889d603f0ec6b1030c91d9033e60525c3

Examinons chacun des paramètres que nous avons donnés à la commande geth.

datadir: Il s’agit de spécifier le répertoire de données comme nous l’avons fait dans les étapes précédentes.

networkid: C’est l’identifiant du réseau, qui différencie notre blockchain privée avec d’autres réseaux Ethereum. Ceci est similaire à la chainId que nous avons définie dans le fichier genesis.json, mais fournit une autre couche de différenciation entre les réseaux. Comme nous pouvons le voir, nous avons utilisé un autre numéro personnalisé pour cette valeur.

ipcdisable: Avec ce paramètre, nous avons désactivé le port de communication interprocessus pour geth de sorte que tout en exécutant plusieurs instances geth (nœuds) sur la même machine locale, nous ne devrions pas rencontrer de problèmes contradictoires.

port: Nous avons sélectionné une valeur personnalisée pour le port afin d’interagir avec geth.

rpc, –rpcapi, –rpcport: Ces trois paramètres définissent la configuration de l’API RPC exposé par geth. Nous voulons l’activer; nous voulons eth,web3,perso nal,net,miner,admin,debug geth ApIs exposés au-dessus de RPC ; et nous voulons l’exécuter sur un port 8507 personnalisé.

mine – minerthreads – etherbase: Avec ces trois paramètres, nous demandons à geth de commencer ce nœud comme un nœud mineur, limiter les fils de processus de mineur à un seul (de sorte que nous ne consommons pas beaucoup de puissance CPU), et envoyer les récompenses du minage au compte Ethereum que nous avons créé dans la première étape.

C’est toute la configuration dont nous avons besoin à ce moment pour exécuter notre premier nœud geth pour le réseau privé.

Lorsque nous exécutons cette commande avec tous les paramètres, geth donnera la sortie suivante (comme dans la capture d’écran montrée dans la figure 6-3).

Figure 6-3. Lancer le Geth du premier nœud

Notez l’auditeur UDP jusqu’à l’instruction de journal dans la sortie.

INFO [02-11|18:00:57] UDP listener up

self=enode://e03b50e9b1b2579904f2bbdff7dd0826bd4e4eb2e

225c1d1cb1a765195474d7418f3e8fbfeefd55bd85722973d1762

6f0e53208c62e38d1099bb583e702b3b48@[::]:30307

Cela contient l’adresse du nœud que nous venons de commencer. Pour connecter d’autres nœuds à ce nœud, nous aurons besoin de cette adresse. Gardons-le à un endroit. La ligne suivante a l’adresse extraite de l’instruction journal précédente.

enode://e03b50e9b1b2579904f2bbdff7dd0826bd4e4eb2e225c1d1cb1a7 65195474d7418f3e8fbfeefd55bd85722973d17626f0e53208c62e38d1099 bb583e702b3b48@[::]:30307

Notez le [::] avant le numéro de port que nous avons défini dans la commande. Remplaçons-le par l’adresse IP de l’hôte local si nous lançons l’autre nœud sur la même machine, ou bien le remplacer par l’adresse IP externe de la machine. Comme nous allons exécuter l’autre nœud réseau sur la même machine (à des fins de développement), nous allons le remplacer par l’adresse IP localhost. Ainsi, l’adresse du premier nœud sera :

enode://e03b50e9b1b2579904f2bbdff7dd0826bd4e4eb2e225c1d1cb1a 765195474d7418f3e8fbfeefd55bd85722973d17626f0e53208c62e38d1099bb583e702b3b48@127.0.0.1:30307

Exécuter le deuxième nœud du réseau

Il n’y a pas de réseau avec un seul nœud; il devrait au moins avoir deux nœuds. Donc, nous allons exécuter une autre instance geth sur la même machine, qui interagira avec le nœud que nous venons de commencer, et ces deux nœuds ensemble formeront notre réseau privé Ethereum.

Pour exécuter un autre nœud, tout d’abord nous avons besoin d’un autre répertoire qui peut être fixé comme répertoire de données du deuxième nœud. Créons-en un.

mkdir mygeth2

Maintenant, nous allons initialiser ce nœud aussi avec la même configuration genesis.json que nous avons créé pour le premier nœud. Créons une autre copie de ce fichier genesis.json et enregistron là dans le nouveau répertoire que nous avons créé plus tôt. Nous allons nous déplacer dans ce répertoire. Maintenant, nous allons initialiser la configuration de genèse pour le deuxième nœud.

sudo geth –datadir “/mygeth2” init genesis.json

Et, nous obtiendrons une sortie similaire que nous avons obtenu pour le premier nœud. Voir la capture d’écran ci-dessous (figure 6-4).

Figure 6-4. Initialisation du Geth de la configuration pour le deuxième nœud

Maintenant, notre deuxième nœud est également initialisée avec la configuration de genèse. Faisons-le.

Pour l’exécution du deuxième nœud, nous passerons quelques paramètres différents à la commande geth. Ce deuxième nœud ne fonctionnera pas en tant que mineur, donc nous allons sauter les trois derniers paramètres de la commande que nous avons donnée au premier nœud.

Aussi, nous voulons exposer la console geth tout en exécutant ce nœud, donc nous allons ajouter un paramètre pour cela. La commande pour l’exécution du deuxième nœud sera :

sudo geth –datadir “/mygeth2” –networkid 8956 –ipcdisable
–port 30308 –rpc –rpcapi “eth,web3,personal,net,miner,admin,
debug” –rpcport 8508 console

Comme nous pouvons le voir, le répertoire des données et les ports ont été modifiés pour le deuxième nœud. Nous avons également ajouté le flag de la console à la commande afin que nous puissions obtenir la console geth pour ce nœud.

Lorsque nous exécuterons cette commande, le deuxième nœud commencera également à s’exécuter et nous verrons la sortie suivante dans le terminal (figure 6-5).

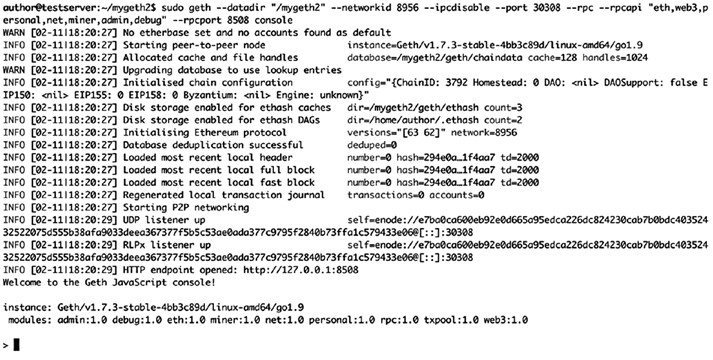
Figure 6-5. Execution du Geth du deuxième nœud

En ce moment, nos deux nœuds geth sont en cours d’exécution, mais ils ne savent rien les uns des autres. Si nous exécutons la commande admin.peers sur la console geth du deuxième nœud, nous obtiendrons un tableau vide en conséquence (figure 6-6).

Figure 6-6. Console Geth—vérifiez s’il y a des pairs

Cela signifie que les nœuds ne sont pas reliés les uns aux autres. Connectons les nœuds. Pour ce faire, nous enverrons la commande admin.addPeer() sur la console geth du deuxième nœud avec l’adresse noeud du premier nœud comme paramètre. Rappelez-vous que nous avons noté l’adresse du premier nœud après l’avoir fait fonctionner. Entrons cette commande dans la console geth du deuxième nœud.

admin.addPeer(“enode://e03b50e9b1b2579904f2bbdff7dd0826bd4e4e b2e225c1d1cb1a7 65195474d7418f3e8fbfeefd55bd85722973d17626f0e5 3208c62e38d1099bb583e702b3b48@127.0.0.1:30307”)

Et dès que nous lançons cette commande sur le deuxième nœud, elle retourne TRUE. En outre, après quelques secondes, il commence la synchronisation avec le premier nœud. La capture d’écran suivante (figure 6-7) montre cette sortie à partir de la console du deuxième nœud.

Figure 6-7. Console Geth—ajouter noeud peer

Nos deux nœuds sont maintenant connectés et notre réseau privé Ethereum est en place. Pour vérifier davantage cela, nous exécuterons la commande admin.peers à nouveau sur le deuxième nœud et cette fois nous verrons le tableau JSON avec un objet affichant le premier nœud en tant que peer (figure 6-8).

Figure 6-8. Console Geth – Vérifier pour les peers (encore une fois)

La capture d’écran suivante montre les fenêtres terminales des deux nœuds que nous avons mis en place. Sur la gauche est le premier nœud, qui est aussi un nœud de minage, et comme nous pouvons le voir, il est constamment en exploitation de nouveaux blocs. Le deuxième nœud est sur la droite et nous pouvons voir qu’il se synchronise avec le premier nœud. La capture d’écran (figure 6-9) est trop petite pour être lue à cause du trop grand nombre d’informations, mais on voit que la capture montre juste les journaux des deux nœuds Ethereum côte à côte.

Figure 6-9. Journaux Geth des deux nœuds Ethereum

Maintenant que les deux nœuds sont connectés l’un à l’autre dans le réseau, nous avons une blockchain Ethereum privée de travail avec deux nœuds. Nous avons également un compte Ethereum qui est établi comme un mineur et est également préfinancé par un certain montant Ether. Nous pouvons maintenant créer plus de comptes et passer Ether parmi eux sur cette blockchain privée.

Dans cette section, nous avons appris à mettre en place un réseau privé Ethereum avec deux nœuds. Cela peut être n’importe quel nombre de nœuds; nous avons juste besoin de suivre le même processus pour chaque nouveau nœud. En cas de nœuds distants, nous devons être prudents en précisant les bonnes adresses IP des machines distantes et nous devons également nous assurer que les ports requis sont ouverts s’il y a un pare-feu empêchant le trafic vers les machines.

Création du contrat intelligent

Maintenant que nous avons le réseau privé Ethereum mis en place et qu’il fonctionne, nous pouvons passer à l’étape suivante dans la création d’un contrat intelligent pour la fonctionnalité de sondage de notre DApp. Nous allons ensuite déployer ce contrat sur notre réseau privé. Nous suivrons les mêmes étapes de la création et du déploiement d’un contrat intelligent tel que nous l’avons fait dans le dernier chapitre.

Maintenons, utilisons notre IDE en ligne Remix et codons notre contrat intelligent dans Solidity.

L’extrait de code Solidity suivant montre le contrat intelligent que nous avons codé pour la fonctionnalité de sondage.

pragma solidity ^0.4.19;

contract Poll {

event Voted(

address _voter,

uint _value

);

mapping(address => uint) public votes;

string pollSubject = “Should coffee be made tax free? Pass 1 for yes OR 2 for no in the vote function.”;

function getPoll() constant public returns (string) {

return pollSubject;

}

function vote(uint selection) public {

Voted(msg.sender, selection);

require (votes[msg.sender] == 0);

require (selection > 0 && selection < 3);

votes[msg.sender] = selection;

}

}

Maintenant, nous allons analyser ce code source contrat pour comprendre ce que nous avons fait ici. Comme nous pouvons le voir, le nom du contrat est Poll.

La ligne de code suivante est :

event Voted(

address _voter,

uint _value

);

L’extrait de code précédent est essentiellement la déclaration d’un événement de contrat intelligent qui prend deux paramètres: l’un est du type d’adresse Ethereum et l’autre est du type d’intégriste non signé. Nous avons créé cet événement afin que nous puissions capturer qui a voté quoi dans le sondage. Nous y reviendrons plus tard.

Ensuite, nous avons

mapping(address => uint) public votes;

La ligne de code précédente déclare une cartographie des adresses Ethereum et des entiers non signés. Il s’agit du magasin de données où nous stockerons les adresses des électeurs et leur valeur choisie pour le vote.

Ensuite, nous avons ce qui suit:

string pollSubject = “Should coffee be made tax free? Pass 1 for yes OR 2 for no in the vote function.”;

function getPoll() constant public returns (string) {

return pollSubject;

}

L’extrait de code précédent déclare d’abord une chaîne pour le sujet de vote. En cela, nous posons une question aux électeurs. Et puis nous avons une fonction qui peut retourner la valeur de cette chaîne afin que les électeurs puissent interroger les résultats du sondage.

Et enfin, nous avons la fonction qui implémente la fonctionnalité de vote.

function vote(uint selection) public {

Voted(msg.sender, selection);

require (votes[msg.sender] == 0);

require (selection > 0 && selection < 3);

votes[msg.sender] = selection;

}

Examinez attentivement chaque ligne de l’extrait précédent.

Tout d’abord, dès que nous entrons dans cette fonction, nous lançons l’événement de vote que nous avons créé avec les valeurs de l’adresse de l’expéditeur (électeur) et la valeur qu’il a choisie.

Ensuite, nous limitons un vote par électeur en vérifiant si la valeur du vote est nulle pour l’adresse correspondante dans la cartographie. L’instruction d’exigence est utilisée pour vérifier les conditions en fonction des entrées de l’utilisateur.

Et ensuite nous limitons également, en utilisant l’instruction d’exigence, la valeur de la sélection à 1 ou 2. 1 est un oui et 2 est un non. Et nous avons adopté ces instructions dans la chaîne pollSubject afin que les électeurs sachent quoi faire. La capture d’écran de la figure 6-10 montre le contrat intelligent dans Remix,

Nous avons compilé ce code de contrat à l’aide de Remix et nous avons pris le ABI et bytecode pour le contrat afin que nous puissions le déployer sur notre réseau privé. Nous avons copié le bytecode et ABI à partir des sections respectives dans l’écran d’affichage des détails de l’onglet compilation Remix, exactement comment nous avons fait cela dans le chapitre précédent.

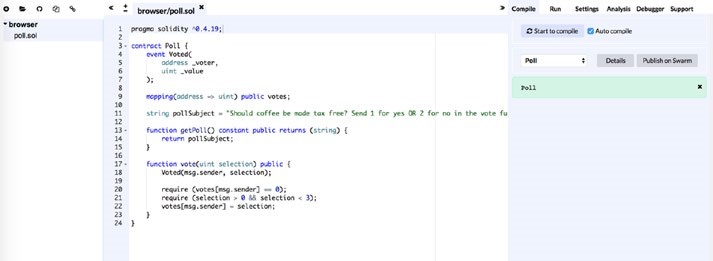
Figure 6-10. Édition de contrat intelligent dans l’éditeur Remix en ligne Solidity

L’ABI du contrat est :

[

{

“constant”: true,

“inputs”: [

{

“name”: “”,

“type”: “address”

}

],

“name”: “votes”,

“outputs”: [

{

“name”: “”,

“type”: “uint256”

}

],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

},

{

“constant”: true,

“inputs”: [],

“name”: “getPoll”,

“outputs”: [

{

“name”: “”,

“type”: “string”

}

],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

},

{

“anonymous”: false,

“inputs”: [

{

“indexed”: false,

“name”: “_voter”,

“type”: “address”

},

{

“indexed”: false,

“name”: “_value”,

“type”: “uint256”

}

],

“name”: “Voted”,

“type”: “event”

},

{

“constant”: false,

“inputs”: [

{

“name”: “selection”,

“type”: “uint256”

}

],

“name”: “vote”,

“outputs”: [],

“payable”: false,

“stateMutability”: “nonpayable”,

“type”: “function”

}

]

Et le code d’octet pour le contrat est

{

“linkReferences”: {},

“object”: 6060604052608060405190810160405280605081526020017f53686f756
c6420636f666666656520626520666206666620662066206620662066620666620666520666520606060616520742074178206000653f2081526020017f53656e64203120666f722076573204f52203220666f7206e6f20696e20468152602020017f6520766f74652066756e63746666f6e20000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000002506001908051906020019061009c9291906100ad565b5034156100a857600080fd5b610152565b828054600181600116156101000203166002900490600052602060002090601f016020900481019282601f106100e57805160ff191683800117855610111c565b828001600101018555821561011c579182015b8281111561011b578251825591602001919060010190610100565b5b509050610129919061012d565b5090565b61014f91905b80821111561014b57600081600090555060010161010133565b5090565b90565b61037380610161600003960000f300606060405260004361061005776000357c0100000000000000000000000000000000000000000000000000000000000000000000900463ffffffff1680630121b93f1461005c57806303c322781461007f578063d8bff5a51461010d5755b600080fd5b341561006777600080fd5b61007d600480803590602001909190505061015a55000341561008a57600080fd5b610092610273565b604051808060200182810382528381815181526020191508051906020019080838360005b83811010156100d257808201518401526020810190506100b75655b50505090505090810190601f16801561000550057808203805160018360200361010000000319168152602019150505b509250505060405180910390f35b341561011857600080fd5b610144600480803573fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff1690602001909190505061031b565b6040518082815260200191505060405180910390f35b7f4d99b957a2bc29a30ebd96a7be8e68fe50a3c701db28a91436490b7d53870ca4382604051808373fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff160008060003373fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff673fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff1681526020019081526020016000205411561021257600080fd5b60008111180118015561022555060038105b151561022d57600080fd5b806000803373fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff190555050565b61027b610333565b60018054600181600161561010101000203166002900480601f016020809104026020200160405190810160405280929190818152602001828054600181600116156101000203166002900480156103115780601f106102e657610100808354040283529160200191610311565b8201919060000526020600020905b8154815290600101906020018083116102f457829003601f168201915b5050505050905090565b6000602052806000526040600020600091509050505481565b6020604051908101604052806000815250905600a165627a7a72305820ec7d3e1dae8412ec85045a8eafc248e37ae506802cc008ead300df1ac81aab490029“,

“opcodes”: “PUSH1 0x60 PUSH1 0x40 MSTORE PUSH1 0x80 PUSH10x40 MLOAD SWAP1
DUP2 ADD PUSH1 0x40 MSTORE DUP1 PUSH1 0x50 DUP2 MSTORE PUSH1 0x20 ADD PUSH32 0x53686F756C6420636F666 66565206265206D61646520746178206672666265653F20 DUP2 MSTORE PUSH1 0x20 ADD PUSH32 0x53656E6420312066F720796573204F52 20322066F72206E6F20696E207468 DUP2 MSTORE PUSH1 0x20 ADD PUSH32 0x6520766F74652066756E6374696F6E2E000000000000000000000000000000000000DUP2 MSTORE POP PUSH1 0x1 SWAP1 DUP1 MLOAD SWAP1 PUSH1 0x20 ADD SWAP1 PUSH2 0x9C SWAP3 SWAP2 SWAP1 PUSH2 0xAD JUMP JUMPDEST POP CALLVALUE ISZERO PUSH2 0xA8 JUMPI PUSH1 0x0 DUP1 REVERT JUMPDEST PUSH2 0x152 JUMP JUMPDEST DUP3 DUP1 SLOAD PUSH1 0x1 DUP2 PUSH1 0x1 ET ISZERO PUSH2 0x100 MUL SUB ET PUSH1 0x2 SWAP1 DIV SWAP1 PUSH1 0x0 MSTORE PUSH1 0x20 PUSH1 0x0 KECCAK256 SWAP1 PUSH1 0x1F ADD PUSH1 0x20 SWAP1 DIV DUP2 ADD SWAP3 DUP3 PUSH1 0x1F LT PUSH2 0xEE JUMPI DUP1 MLOAD PUSH1 0xFF PAS ET DUP4 DUP1 ADD OU DUP6 SSTORE PUSH2 0x11C JUMP JUMPDEST DUP3 DUP1 ADD PUSH1 0x1 ADD DUP6 SSTORE DUP3 ISZERO PUSH2 0x11C JUMPI SWAP2 DUP3 ADD JUMPDEST DUP3 DUP2 GT ISZERO PUSH2 0x11B JUMPI DUP3 MLOAD DUP3 SSTORE SWAP2 PUSH1 0x20 ADD SWAP2 SWAP1 PUSH1 0x1 ADD SWAP1 PUSH2 0x100 JUMP JUMPDEST JUMPDEST POP SWAP1 POP PUSH2 0x129 SWAP2 SWAP1 PUSH2 0x12D JUMP JUMPDEST POP SWAP1 JUMP JUMPDEST PUSH2 0x14F SWAP2 SWAP1 JUMPDEST DUP1 DUP3 GT ISZERO PUSH2 0x14B JUMPI PUSH1 0x0 DUP2 PUSH1 0x0 SWAP1 SSTORE POP PUSH1 0x1 ADD PUSH2 0x133 JUMP JUMPDEST POP SWAP1 JUMP JUMPDEST SWAP1 JUMP JUMPDEST PUSH2 0x373 DUP1 PUSH2 0x161 PUSH1 0x0 CODECOPY PUSH1 0x0 RETURN STOP PUSH1 0x60 PUSH1 0x40 MSTORE PUSH1 0x4 CALLDATASIZE LT PUSH2 0x57 JUMPI PUSH1 0x0 CALLDATALOAD PUSH29 0x1000000000000000000000000000000000000000000000000000000000000000000000000000SWAP1 DIV PUSH4 0xFFFFFFFF ET DUP1 PUSH4 0x121B93F EQ PUSH2 0x5C JUMPI DUP1 PUSH4 0x3C32278 EQ PUSH2 0x7F JUMPI DUP1 PUSH4 0xD8BFF5A5 EQ PUSH2 0x10D JUMPI JUMPDEST PUSH1 0x0 DUP1 REVERT JUMPDEST CALLVALUE ISZERO PUSH2 0x67 JUMPI PUSH1 0x0 DUP1 REVERT JUMPDEST PUSH2 0x7D PUSH1 0x4 DUP1 DUP1 CALLDATALOAD SWAP1 PUSH1 0x20 ADD SWAP1 SWAP2 SWAP1 POP POP PUSH2 0x15A JUMP JUMPDEST STOP JUMPDEST CALLVALUE ISZERO PUSH2 0x8A JUMPI PUSH1 0x0 DUP1 REVERT JUMPDEST PUSH2 0x92 PUSH2 0x273 JUMP JUMPDEST PUSH1 0x40 MLOAD DUP1 DUP1 PUSH1 0x20 ADD DUP3 DUP2 SUB DUP3 MSTORE DUP4 DUP2 DUP2 MLOAD DUP2 MSTORE PUSH1 0x20 ADD SWAP2 POP DUP1 MLOAD SWAP1 PUSH1 0x20 ADD SWAP1 DUP1 DUP4 DUP4 PUSH1 0x0 JUMPDEST DUP4 DUP2 LT ISZERO PUSH2 0xD2 JUMPI DUP1 DUP3 ADD MLOAD DUP2 DUP5 ADD MSTORE PUSH1 0x20 DUP2 ADD SWAP1 POP PUSH2 0xB7 JUMP JUMPDEST POP POP POP POP SWAP1 POP SWAP1 DUP2 ADD SWAP1 PUSH1 0x1F ET DUP1 ISZERO PUSH2 0xFF JUMPI DUP1 DUP3 SUB DUP1 MLOAD PUSH1 0x1 DUP4 PUSH1 0x20 SUB PUSH2 0x100 EXP SUB NOT ET DUP2 MSTORE PUSH1 0x20 ADD SWAP2 POP JUMPDEST POP SWAP3 POP POP POP PUSH1 0x40 MLOAD DUP1 SWAP2 SUB SWAP1 RETURN JUMPDEST CALLVALUE ISZERO PUSH2 0x118 JUMPI PUSH1 0x0 DUP1 REVERT JUMPDEST PUSH2 0x144 PUSH1 0x4 DUP1 DUP1 CALLDATALOAD PUSH20 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF FFF ET SWAP1 PUSH1 0x20 ADD SWAP1 SWAP2 SWAP1 POP POP PUSH2 0x31B JUMP JUMPDEST PUSH1 0x40 MLOAD DUP1 DUP3 DUP2 MSTORE PUSH1 0x20 ADD SWAP2 POP POP PUSH1 0x40 MLOAD DUP1 SWAP2 SUB SWAP1 RETURN JUMPDEST PUSH32 0x4D99B9577A2BC29A30EBD96A7BE8E68FE50A3C701DB28A91436490B7 D53870CA4 CALLER DUP3 PUSH1 0x40 MLOAD DUP1 DUP4 PUSH20 0xF FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF AND PUSH20 0xFFFF FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF AND DUP2 MSTORE PUSH1 0x20 ADD DUP3 DUP2 MSTORE PUSH1 0x20 ADD SWAP3 POP POP PUSH1 0x40 MLOAD DUP1 SWAP2 SUB SWAP1 LOG1 PUSH1 0x0 DUP1 PUSH1 0x0 CALLER PUSH20 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF ET PUSH20 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF FFFFFFF ET DUP2 MSTORE PUSH1 0x20 ADD SWAP1 DUP2 MSTORE PUSH1 0x20 ADD PUSH1 0x0 KECCAK256 SLOAD EQ ISZERO ISZERO PUSH2 0x212 JUMPI PUSH1 0x0 DUP1 REVERT JUMPDEST PUSH1 0x0 DUP2 GT DUP1 ISZERO PUSH2 0x222 JUMPI POP PUSH1 0x3 DUP2 LT JUMPDEST ISZERO ISZERO PUSH2 0x22D JUMPI PUSH1 0x0 DUP1 REVERT JUMPDEST DUP1 PUSH1 0x0 DUP1 CALLER PUSH20 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF AND PUSH20 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF FFF FFF ET DUP2 MSTORE PUSH1 0x20 ADD SWAP1 DUP2 MSTORE PUSH1 0x20 ADD PUSH1 0x0 KECCAK256 DUP2 SWAP1 SSTORE POP POP JUMP JUMPDEST PUSH2 0x27B PUSH2 0x333 JUMP JUMPDEST PUSH1 0x1 DUP1 SLOAD PUSH1 0x1 DUP2 PUSH1 0x1 ET ISZERO PUSH2 0x100 MUL SUB ET PUSH1 0x2 SWAP1 DIV DUP1 PUSH1 0x1F ADD PUSH1 0x20 DUP1 SWAP2 DIV MUL PUSH1 0x20 ADD PUSH1 0x40 MLOAD SWAP1 DUP2 ADD PUSH1 0x40 MSTORE DUP1 SWAP3 SWAP2 SWAP1 DUP2 DUP2 MSTORE PUSH1 0x20 ADD DUP3 DUP1 SLOAD PUSH1 0x1 DUP2 PUSH1 0x1 ET ISZERO PUSH2 0x100 MUL SUB ET PUSH1 0x2 SWAP1 DIV DUP1 ISZERO PUSH2 0x311 JUMPI DUP1 PUSH1 0x1F LT PUSH2 0x2E6 JUMPI PUSH2 0x100 DUP1 DUP4 SLOAD DIV MUL DUP4 MSTORE SWAP2 PUSH1 0x20 ADD SWAP2 PUSH2 0x311 JUMP JUMPDEST DUP3 ADD SWAP2 SWAP1 PUSH1 0x0 MSTORE PUSH1 0x20 PUSH1 0x0 KECCAK256 SWAP1 JUMPDEST DUP2 SLOAD DUP2 MSTORE SWAP1 PUSH1 0x1 ADD SWAP1 PUSH1 0x20 ADD DUP1 DUP4 GT PUSH2 0x2F4 JUMPI DUP3 SWAP1 SUB PUSH1 0x1F ET DUP3 ADD SWAP2 JUMPDEST POP POP POP POP SWAP1 POP SWAP1 JUMP JUMPDEST PUSH1 0x0 PUSH1 0x20 MSTORE DUP1 PUSH1 0x0 MSTORE PUSH1 0x40 PUSH1 0x0 KECCAK256 PUSH1 0x0 SWAP2 POP SWAP1 POP SLOAD DUP2 JUMP JUMPDEST PUSH1 0x20 PUSH1 0x40 MLOAD SWAP1 DUP2 ADD PUSH1 0x40 MSTORE DUP1 PUSH1 0x0 DUP2 MSTORE POP SWAP1 JUMP STOP LOG1 PUSH6 0x627A7A723058 KECCAK256 0cheque PUSH30 0x3E1DAE8412EC85045A8EAFC248E37AE506802CC008EAD300DF1AC81A AB49 STOP 0x29 “,
“sourceMap”: “26:576:0:-;; 167:103;;;;;;;;;;;;;;;;;;;;;;;; ;;;;;;;;;;;;;;;;;;::::i;:::;;; 26:576;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;::::i;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;a.a.
;;;;;;;;;;;;;;::::::::::::::::;;;;;;;;;

}

Avec ces valeurs, notre contrat intelligent est prêt à être déployé.

Il peut y avoir quelques améliorations qui peuvent être apportées pour rendre ce contrat plus sûr et plus convivial pourla performance(gas).le code Solidity ne doit pas être pris comme référence. Pour les meilleures pratiques de Solidity, nous vous recommandons de suivre la documentation officielle de solidité et les textes spécifiques à la solidité.

Déploiement du contrat intelligent

Dans cette section, nous allons déployer le contrat intelligent que nous avons développé dans la dernière section pour le réseau privé Ethereum que nous avons créé. Le processus de déploiement du contrat intelligent est le même que ce que nous avons fait dans le chapitre précédent. La seule différence est que cette fois, nous déployons le contrat sur un réseau privé au lieu d’un réseau public. Dans ce chapitre aussi, nous utilisons la même bibliothèque web3.js pour la programmation Ethereum en utilisant JavaScript. Nous recommandons au lecteur de passer en revue le chapitre précédent s’il ne l’a pas déjà fait.

Mise en place de la bibliothèque et de la connexion web3

Tout d’abord, nous installerons la bibliothèque web3 dans une application node.js. C’est exactement ce que nous avons fait dans le dernier chapitre. Cette application node.js sera utilisée pour déployer le contrat intelligent.

npm installer web3@1.0.0-bêta.28

Après l’installation, nous allons d’abord initialiser et instantanément l’instance web3.

var Web3 = require(‘web3’);

var web3 = new Web3(new Web3.providers.HttpProvider(‘http://127.0.0.1:8507’));

Notez que cette fois, notre fournisseur HTTP pour l’instance web3 a changé pour un point de terminaison local au lieu d’un point de terminaison INFURA public, que nous avons utilisé dans le dernier chapitre. C’est parce que nous sommes maintenant en connexion avec un réseau privé local. Notez également que le port que nous utilisons est 8507, qui est ce que nous avons fourni dans le paramètre –rpcport lorsque nous avons mis en place le premier nœud de notre réseau privé.

Cela signifie que nous nous connectons au premier nœud du réseau à partir de notre instance web3.

Déployer le contrat sur le réseau privé

Maintenant que nous avons notre contrat intelligent et ses détails, nous allons préparer un objet de contrat web3 avec les détails de ce contrat, puis nous allons déployer ce contrat à la blockchain Ethereum en appelant la méthode de déploiement sur l’objet du contrat.

Nous avons besoin de créer un objet de la classe web3.eth.Contract qui peut représenter notre contrat. L’extrait de code suivant crée une instance de contrat avec l’ABI de notre contrat comme entrée au constructeur.

var pollingContract = new web3.eth.Contract([

{

“constant”: true,

“inputs”: [

{

“name”: “”,

“type”: “address”

}

],

“name”: “votes”,

“outputs”: [

{

“name”: “”,

“type”: “uint256”

}

],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

},

{

“constant”: true,

“inputs”: [],

“name”: “getPoll”,

“outputs”: [

{

“name”: “”,

“type”: “string”

}

],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

},

{

“anonymous”: false,

“inputs”: [

{

“indexed”: false,

“name”: “_voter”,

“type”: “address”

},

{

“indexed”: false,

“name”: “_value”,

“type”: “uint256”

}

],

“name”: “Voted”,

“type”: “event”

},

{

“constant”: false,

“inputs”: [

{

“name”: “selection”,

“type”: “uint256”

}

],

“name”: “vote”,

“outputs”: [],

“payable”: false,

“stateMutability”: “nonpayable”,

“type”: “function”

}

]);

Maintenant, nous devons déployer ce contrat sur le réseau Ethereum en utilisant la méthode de déploiement de la bibliothèque web3. L’extrait de code suivant montre comment le faire. Dans cet extrait, nous avons ajouté le code octet dans le champ de données de l’objet passé à la méthode de déploiement.

pollingContract

.deploy({

data: ‘0x6060604052608060405190810160405280605060508152602
0017f53686f756c6420636f66666520626265206d6164652074617 820667266653f2081526020017f53656e64203120666f720796573204f52203220666f72206e6f20696e207468152602017f6520766f74652066756e6374696f6e2e00000000000000000000000000000000000000000008152506001908051906020019061009c9291906100ad565b5034156100a857600080fd5b610152565b828054600181600116156101000203166002004906000526020202090601f0160209004810192826010101010600e5705050516082800160010101855521561111c579182015b82811111111111105782518255591602020191906001010190610005555b5b50061012d565b5090565b61014f91905b808211561014b576000816000905550600101610133565b5090565b90565b61037380610161616000396000f300606060405260043610610005776000357c0100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000606301222201221222122122122122121221221221212212123380633bff5a51461010575b6000080fd5b34156100677600080fd5b61007d6007d60080303590602000190190505060677600080fd5b61007d600600600600060006003035590602000190505041561008a57600080fd5b6100922610273565b60405180806020018281038252838181118115260200191508001906020019080838360005b83811010101010257008201518065b50505050905090810190601f1680156100ff57808203805160018360200361010000031916815220200191505b509250505060405180910390f35b3415610118577600080fd5b6101446000480803573fffffffffffffffffffffffffffffffffffffffffffffffffffffff1690201909190505061031b565b60405180281520202020019191500f35b7f4d9b957a2bc29a30ebd96a7be8e68fe50a3c701db28a91436490b7d53870ca43382604051808373ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff16822020281522020200192250505060405180a160008060003373fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff168152602001908152602001600020541151561021257600080fd5b600081118015610222570600381105b1561022d57600080fd5b806000803373ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff1673ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff1673ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff1673ffffffffffffffffffffffffffffffffffffffffffffffff1681526020201526020016002081905550505050555055555555555555555555555555555065027b61033565b60018055460018160011615610100020316002900480601f0160208091040260200160405190810160405280929190818152602001828054600181600116156101000020316002900480156103115780601f106102e657610100808354040283529160200191610311565b820191906000526020600020905b8154815290600101906020018083116102f457829003601f168201915b50505050905090565b60006020528060005260406000206000915090505481565b6020604051908101604052806000815250905600a165627a7a72305820ec7d3e1dae8412ec85045a8eafc248e37ae506802cc008ead300df1ac81aab490029‘

})

.send({

from: ‘0xbaf735f889d603f0ec6b1030c91d9033e60525c3’,

gas: 4700000,

gasPrice: ‘20000000000000’

},

function(error, transactionHash){

console.log(error);

console.log(transactionHash);

})

.then(function(contract){

console.log(contract);

});

Notez que nous avons également utilisé le compte que nous avons créé lors de la configuration du réseau dans le champ “à partir” de la fonction d’envoi. Comme ce compte a été préfinancé avec neuf Éthers et il est également ajouté comme le compte étherbase pour les récompenses de minage, il a assez d’éther pour déployer un contrat. La fonction complète de déploiement du contrat sera

var deployContract = function () {

var pollingContract = new web3.eth.Contract([{

“constant”: true,

“inputs”: [{

“name”: “”,

“type”: “address”

}],

“name”: “votes”,

“outputs”: [{

“name”: “”,

“type”: “uint256”

}],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

},

{

“constant”: true,

“inputs”: [],

“name”: “getPoll”,

“outputs”: [{

“name”: “”,

“type”: “string”

}],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

},

{

“anonymous”: false,

“inputs”: [{

“indexed”: false,

“name”: “_voter”,

“type”: “address”

},

{

“indexed”: false,

“name”: “_value”,

“type”: “uint256”

}

],

“name”: “Voted”,

“type”: “event”

},

{

“constant”: false,

“inputs”: [{

“name”: “selection”,

“type”: “uint256”

}],

“name”: “vote”,

“outputs”: [],

“payable”: false,

“stateMutability”: “nonpayable”,

“type”: “function”

}

]);

pollingContract

.deploy({

data: ‘0x6060604052608060405190810160405280605081526020017f53686f7
56c6420636f66666565206265206d6164652074617820667265653f2081526020017f53656e64203120666f7220796573204f52203220666f72206e6f20696e20746881526020017f6520766f74652066756e6374696f6e2e000000000000000000000000000000008152506001908051906020019061009c9291906100ad565b5034156100a857600080fd5b610152565b828054600181600116156101000203166002900490600052602060002090601f016020900481019282601f106100ee57805160ff191683800117855561011c565b8280016001018555821561011c579182015b8281111561011b578251825591602001919060010190610100565b5b509050610129919061012d565b5090565b61014f91905b8082111561014b576000816000905550600101610133565b5090565b90565b610373806101616000396000f300606060405260043610610057576000357c0100000000000000000000000000000000000000000000000000000000900463ffffffff1680630121b93f1461005c57806303c322781461007f578063d8bff5a51461010d575b600080fd5b341561006757600080fd5b61007d600480803590602001909190505061015a565b005b341561008a57600080fd5b610092610273565b6040518080602001828103825283818151815260200191508051906020019080838360005b838110156100d25780820151818401526020810190506100b7565b50505050905090810190601f1680156100ff5780820380516001836020036101000a031916815260200191505b509250505060405180910390f35b341561011857600080fd5b610144600480803573ffffffffffffffffffffffffffffffffffffffff1690602001909190505061031b565b6040518082815260200191505060405180910390f35b7f4d99b957a2bc29a30ebd96a7be8e68fe50a3c701db28a91436490b7d53870ca43382604051808373ffffffffffffffffffffffffffffffffffffffff1673ffffffffffffffffffffffffffffffffffffffff1681526020018281526020019250505060405180910390a160008060003373ffffffffffffffffffffffffffffffffffffffff1673ffffffffffffffffffffffffffffffffffffffff1681526020019081526020016000205414151561021257600080fd5b6000811180156102225750600381105b151561022d57600080fd5b806000803373ffffffffffffffffffffffffffffffffffffffff1673ffffffffffffffffffffffffffffffffffffffff1681526020019081526020016000208190555050565b61027b610333565b60018054600181600116156101000203166002900480601f0160208091040260200160405190810160405280929190818152602001828054600181600116156101000203166002900480156103115780601f106102e657610100808354040283529160200191610311565b820191906000526020600020905b8154815290600101906020018083116102f457829003601f168201915b5050505050905090565b60006020528060005260406000206000915090505481565b6020604051908101604052806000815250905600a165627a7a72305820ec7d3e1dae8412ec85045a8eafc248e37ae506802cc008ead300df1ac81aab490029’

})

.send({

from: ‘0xbaf735f889d603f0ec6b1030c91d9033e60525c3’,

gas: 4700000,

gasPrice: ‘20000000000000’

},

function (error, transactionHash) {

console.log(error);

console.log(transactionHash);

})

.then(function (contract) {

console.log(contract);

});

};

Après l’exécution de cette fonction à partir de notre application node.js, nous avons reçu la sortie suivante :

Contract {

currentProvider: [Getter/Setter],

_requestManager:

RequestManager {

provider: null,

providers:

{ WebsocketProvider: [Function: WebsocketProvider],

HttpProvider: [Function: HttpProvider],

IpcProvider: [Function: IpcProvider] },

subscriptions: {} },

givenProvider: null,

providers:

{ WebsocketProvider: [Function: WebsocketProvider],

HttpProvider: [Function: HttpProvider],

IpcProvider: [Function: IpcProvider] },

_provider: null,

setProvider: [Function],

BatchRequest: [Function: bound Batch],

extend:

{ [Function: ex]

formatters:

{ inputDefaultBlockNumberFormatter: [Function:

inputDefaultBlockNumberFormatter],

inputBlockNumberFormatter: [Function:

inputBlockNumberFormatter],

inputCallFormatter: [Function: inputCallFormatter],

inputTransactionFormatter: [Function:

inputTransactionFormatter],

inputAddressFormatter: [Function:

inputAddressFormatter],

inputPostFormatter: [Function: inputPostFormatter],

inputLogFormatter: [Function: inputLogFormatter],

inputSignFormatter: [Function: inputSignFormatter],

outputBigNumberFormatter: [Function:

outputBigNumberFormatter],

outputTransactionFormatter: [Function:

outputTransactionFormatter],

outputTransactionReceiptFormatter: [Function:

outputTransactionReceiptFormatter],

outputBlockFormatter: [Function: outputBlockFormatter],

outputLogFormatter: [Function: outputLogFormatter],

outputPostFormatter: [Function: outputPostFormatter],

outputSyncingFormatter: [Function:

outputSyncingFormatter] },

utils:

{ _fireError: [Function: _fireError],

_jsonInterfaceMethodToString: [Function:

_jsonInterfaceMethodToString],

randomHex: [Function: randomHex],

_: [Function],

BN: [Function],

isBN: [Function: isBN],

isBigNumber: [Function: isBigNumber],

isHex: [Function: isHex],

isHexStrict: [Function: isHexStrict],

sha3: [Function],

keccak256: [Function],

soliditySha3: [Function: soliditySha3],

isAddress: [Function: isAddress],

checkAddressChecksum: [Function: checkAddressChecksum],

toChecksumAddress: [Function: toChecksumAddress],

toHex: [Function: toHex],

toBN: [Function: toBN],

bytesToHex: [Function: bytesToHex],

hexToBytes: [Function: hexToBytes],

hexToNumberString: [Function: hexToNumberString],

hexToNumber: [Function: hexToNumber],

toDecimal: [Function: hexToNumber],

numberToHex: [Function: numberToHex],

fromDecimal: [Function: numberToHex],

hexToUtf8: [Function: hexToUtf8],

hexToString: [Function: hexToUtf8],

toUtf8: [Function: hexToUtf8],

utf8ToHex: [Function: utf8ToHex],

stringToHex: [Function: utf8ToHex],

fromUtf8: [Function: utf8ToHex],

hexToAscii: [Function: hexToAscii],

toAscii: [Function: hexToAscii],

asciiToHex: [Function: asciiToHex],

fromAscii: [Function: asciiToHex],

unitMap: [Object],

toWei: [Function: toWei],

fromWei: [Function: fromWei],

padLeft: [Function: leftPad],

leftPad: [Function: leftPad],

padRight: [Function: rightPad],

rightPad: [Function: rightPad],

toTwosComplement: [Function: toTwosComplement] },

Method: [Function: Method] },

clearSubscriptions: [Function],

options:

{ address: [Getter/Setter],

jsonInterface: [Getter/Setter],

data: undefined,

from: undefined,

gasPrice: undefined,

gas: undefined },

defaultAccount: [Getter/Setter],

defaultBlock: [Getter/Setter],

methods:

{ votes: [Function: bound _createTxObject],

‘0xd8bff5a5’: [Function: bound _createTxObject],

‘votes(address)’: [Function: bound _createTxObject],

getPoll: [Function: bound _createTxObject],

‘0x03c32278’: [Function: bound _createTxObject],

‘getPoll()’: [Function: bound _createTxObject],

vote: [Function: bound _createTxObject],

‘0x0121b93f’: [Function: bound _createTxObject],

‘vote(uint256)’: [Function: bound _createTxObject] },

events:

{ Voted: [Function: bound ],

‘0x4d99b957a2bc29a30ebd96a7be8e68fe50a3c701db28a91436490b7d53870ca4’: [Function: bound ],

‘Voted(address,uint256)’: [Function: bound ],

allEvents: [Function: bound ] },

_address: ‘0x59E7161646C3436DFdF5eBE617B4A172974B481e’,

_jsonInterface:

[ { constant: true,

inputs: [Array],

name: ‘votes’,

outputs: [Array],

payable: false,

stateMutability: ‘view’,

type: ‘function’,

signature: ‘0xd8bff5a5’ },

{ constant: true,

inputs: [],

name: ‘getPoll’,

outputs: [Array],

payable: false,

stateMutability: ‘view’,

type: ‘function’,

signature: ‘0x03c32278’ },

{ anonymous: false,

inputs: [Array],

name: ‘Voted’,

type: ‘event’,

signature: ‘0x4d99b957a2bc29a30ebd96a7be8e68fe50a3c701db28a91436490b7d53870ca4’ },

{ constant: false,

inputs: [Array],

name: ‘vote’,

outputs: [],

payable: false,

stateMutability: ‘nonpayable’,

type: ‘function’,

signature: ‘0x0121b93f’ } ] }

La sortie montre les différentes propriétés du contrat que nous avons déployé sur notre réseau privé. Le plus important est l’adresse du contrat à laquelle le contrat est déployé, qui est 0x59E7161646C3436DFdF5eBE617B4A172974B481e.

Le contrat ABI et l’adresse peuvent être utilisés pour appeler une fonction sur le contrat. Dans la section suivante, nous allons construire une application web simple qui appellera la fonction de vote de ce contrat, montrant comment le sondage peut être fait à partir de l’extrémité avant.

Client Application

Comme nous l’avons fait dans le dernier chapitre, nous pouvons utiliser la bibliothèque web3 pour appeler une fonction sur un contrat intelligent. Mais, dans le dernier chapitre, nous l’avons fait en utilisant une application node.js et non dans une application de navigateur. Dans cette section, nous utiliserons web3 dans une application de navigateur pour appeler la fonction de vote de notre contrat intelligent déployé.

L’application web la plus simple que nous pouvons créer pour ce DApp est une seule page web avec quelques commandes de texte et de bouton. Pour la page Web, nous pouvons utiliser le code suivant à l’intérieur d’un fichier html, puis l’exécuter à partir d’un serveur local. Notez qu’il est important de charger les scripts à partir d’un serveur local et de ne pas ouvrir directement le fichier depuis le navigateur, sans faire face à des problèmes de sécurité du navigateur.

<html>

<c>

<meta charset=”UTF-8″>

<title>Beginning Blockchain – DApp demo</title>

<script src=”<source of web3 library from any CDN or local file>”></script>

</head>

<body>

<div>

<p>

<strong>Beginning Blockchain</strong>

</p>

<p>Hi, Welcome to the Polling DApp!</p>

<p>&nbsp;</p>

<p>Get latest poll:&nbsp;

<button onclick=”getPoll()”>Get Poll</button>

</p>

<p>

<div id=”pollSubject”></div>

</p>

<p>Vote: Yes:

<input type=”radio” id=”yes”> No:

<input type=”radio” id=”no”>

</p>

<p>Submit:&nbsp;

<button onclick=”submitVote()”>Submit Vote</button>

</p>

</p>

</div>

<script>

if (typeof web3 !== ‘undefined’) {

web3 = new Web3(web3.currentProvider);

} else {

web3 = new Web3(new Web3.providers.HttpProvider

(‘http://127.0.0.1:8507’));

}

function getPoll() {

var pollingContract = new web3.eth.Contract([{

“constant”: true,

“inputs”: [{

“name”: “”,

“type”: “address”

}],

“name”: “votes”,

“outputs”: [{

“name”: “”,

“type”: “uint256”

}],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

},

{

“constant”: true,

“inputs”: [],

“name”: “getPoll”,

“outputs”: [{

“name”: “”,

“type”: “string”

}],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

},

{

“anonymous”: false,

“inputs”: [{

“indexed”: false,

“name”: “_voter”,

“type”: “address”

},

{

“indexed”: false,

“name”: “_value”,

“type”: “uint256”

}

],

“name”: “Voted”,

“type”: “event”

},

{

“constant”: false,

“inputs”: [{

“name”: “selection”,

“type”: “uint256”

}],

“name”: “vote”,

“outputs”: [],

“payable”: false,

“stateMutability”: “nonpayable”,

“type”: “function”

}

], ‘0x59E7161646C3436DFdF5eBE617B4A172974B481e’);

pollingContract.methods.getPoll().call().

then(function (value) {

document.getElementById(‘pollSubject’).

textContent = value;

});

};

function submitVote() {

var value = 0

var yes = document.getElementById(‘yes’).checked;

var no = document.getElementById(‘no’).checked;

if (yes) {

value = 1

} else if (no) {

value = 2

} else {

return;

}

var pollingContract = new web3.eth.Contract([{

“constant”: true,

“inputs”: [{

“name”: “”,

“type”: “address”

}],

“name”: “votes”,

“outputs”: [{

“name”: “”,

“type”: “uint256”

}],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

},

{

“constant”: true,

“inputs”: [],

“name”: “getPoll”,

“outputs”: [{

“name”: “”,

“type”: “string”

}],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

},

{

“anonymous”: false,

“inputs”: [{

“indexed”: false,

“name”: “_voter”,

“type”: “address”

},

{

“indexed”: false,

“name”: “_value”,

“type”: “uint256”

}

],

“name”: “Voted”,

“type”: “event”

},

{

“constant”: false,

“inputs”: [{

“name”: “selection”,

“type”: “uint256”

}],

“name”: “vote”,

“outputs”: [],

“payable”: false,

“stateMutability”: “nonpayable”,

“type”: “function”

}

], ‘0x59E7161646C3436DFdF5eBE617B4A172974B481e’);

pollingContract.methods.vote(value).send({

from: ‘0xbaf735f889d603f0ec6b1030c91d9033e60525c3’

}).then(function (result) {

console.log(result);

});

};

</script>

</body>

</html>

Analysons maintenant chacune des sections de ce fichier HTML.

Dans la section principale du document HTML, nous avons chargé le script web3 à partir d’une source CDN ou d’une source locale. C’est comme si nous nous référons à n’importe quelle autre bibliothèque JavaScript tierce dans nos pages Web (JQuery, etc.)

Ensuite, dans la section corps du HTML, nous avons les contrôles pour afficher le sujet du sondage et la radio et soumettre des boutons pour capturer l’entrée de l’utilisateur. La page Web globale ressemble à ceci (figure 6-11).

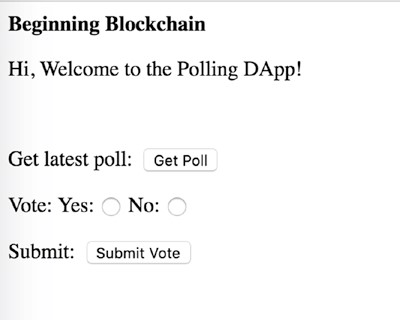
Figure 6-11. Vue d’application Web de sondage

Ce qui est important, c’est la section script dans le corps. C’est là que nous appelons le code d’interaction contractuel intelligent. Examinons-le en détail.

<script>

if (typeof web3 !== ‘undefined’) {

web3 = new Web3(web3.currentProvider);

} else {

web3 = new Web3(new Web3.providers.HttpProvider(‘http://127.0.0.1:8507’));

}

function getPoll() {

var pollingContract = new web3.eth.Contract([{

“constant”: true,

“inputs”: [{

“name”: “”,

“type”: “address”

}],

“name”: “votes”,

“outputs”: [{

“name”: “”,

“type”: “uint256”

}],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

},

{

“constant”: true,

“inputs”: [],

“name”: “getPoll”,

“outputs”: [{

“name”: “”,

“type”: “string”

}],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

},

{

“anonymous”: false,

“inputs”: [{

“indexed”: false,

“name”: “_voter”,

“type”: “address”

},

{

“indexed”: false,

“name”: “_value”,

“type”: “uint256”

}

],

“name”: “Voted”,

“type”: “event”

},

{

“constant”: false,

“inputs”: [{

“name”: “selection”,

“type”: “uint256”

}],

“name”: “vote”,

“outputs”: [],

“payable”: false,

“stateMutability”: “nonpayable”,

“type”: “function”

}

], ‘0x59E7161646C3436DFdF5eBE617B4A172974B481e’);

pollingContract.methods.getPoll().call().

then(function (value) {

document.getElementById(‘pollSubject’).

textContent = value;

});

};

function submitVote() {

var value = 0

var yes = document.getElementById(‘yes’).checked;

var no = document.getElementById(‘no’).checked;

if (yes) {

value = 1

} else if (no) {

value = 2

} else {

return;

}

var pollingContract = new web3.eth.Contract([{

“constant”: true,

“inputs”: [{

“name”: “”,

“type”: “address”

}],

“name”: “votes”,

“outputs”: [{

“name”: “”,

“type”: “uint256”

}],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

},

{

“constant”: true,

“inputs”: [],

“name”: “getPoll”,

“outputs”: [{

“name”: “”,

“type”: “string”

}],

“payable”: false,

“stateMutability”: “view”,

“type”: “function”

},

{

“anonymous”: false,

“inputs”: [{

“indexed”: false,

“name”: “_voter”,

“type”: “address”

},

{

“indexed”: false,

“name”: “_value”,

“type”: “uint256”

}

],

“name”: “Voted”,

“type”: “event”

},

{

“constant”: false,

“inputs”: [{

“name”: “selection”,

“type”: “uint256”

}],

“name”: “vote”,

“outputs”: [],

“payable”: false,

“stateMutability”: “nonpayable”,

“type”: “function”

}

], ‘0x59E7161646C3436DFdF5eBE617B4A172974B481e’);

pollingContract.methods.vote(value).send({

from: ‘0xbaf735f889d603f0ec6b1030c91d9033e60525c3’

}).then(function (result) {

console.log(result);

});

};

</script>

Dans la section de script précédente, nous initialisons d’abord l’objet web3 avec le fournisseur HTTP du nœud Ethereum local (s’il n’est pas déjà initialisé).

Ensuite, nous avons deux fonctions JavaScript. Une pour obtenir la valeur de la chaîne pollSubject du contrat intelligent et une autre pour appeler la fonction de vote du contrat.

L’appel des fonctions de contrat intelligente est exactement comme nous l’avons fait dans le chapitre précédent en utilisant le sous-module web3.eth.Contract de la bibliothèque web3.

Notez que dans la première fonction getPoll nous appelons la fonction call sur l’instance de contrat intelligent, tandis que dans la deuxième fonction submitVote nous appelons send sur l’instance de contrat intelligent. C’est principalement la différence dans les deux appels de fonction.

En utilisant call sur la fonction getPoll du contrat intelligent, nous obtenons la valeur de retour de la fonction getPoll sans envoyer aucune transaction au réseau. Nous montrons ensuite cette valeur sur l’interface triuque en l’attribuant comme texte d’un élément d’interface uI.

Ensuite, en utilisant send sur la fonction de vote, nous envoyons une transaction pour exécuter cette fonction sur le réseau et nous devons donc également définir un compte qui sera utilisé pour exécuter la fonction de contrat intelligent. Voici la sortie obtenue à partir de la fonction submitVote montrée précédemment, qui est essentiellement un reçu de transaction.

{

blockHash: ‘0x04a02dd56c037569eb6abe25e003a65d3366407134c
90a056f64b62c2d23eb84’,
blockNumber: 4257,
contractAddress: null,
cumulativeGasUsed: 43463,
from: ‘0xbaf735f889d603f0ec6b1030c91d9033e60525c3’,
gasUsed: 43463,
logsBloom: ‘0x000000000000000000000000000000008000000000000 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000020000000000200000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000200000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000,
root: ‘0x58bc4ee0a3025ca3f303df9bb243d052a123026519637
30c52c88aafe92ebeee’,
to: ‘0x59e7161646c3436dfdf5ebe617b4a172974b481e’,
transactionHash: ‘0x434aa9c0037af3367a0d3d92985781c50
774241ace1d382a8723985efcea73b3’,
transactionIndex: 0,
events: {

Voted: {

address: ‘0x59E7161646C3436DFdF5eBE617B4A17
2974B481e’,
blockNumber: 4257,
transactionHash: ‘0x434aa9c0037af3367a0d3d929
85781c50774241ace1d382a8723985efcea73b3’,
transactionIndex: 0,
blockHash: ‘0x04a02dd56c037569eb6abe25e003a65
d3366407134c90a056f64b62c2d23eb84’,
logIndex: 0,
removed: false,
id: ‘log_980a1744’,
returnValues: [Result],
event: ‘Voted’,
signature: ‘0x4d99b957a2bc29a30ebd96a7be8e68f
e50a3c701db28a91436490b7d53870ca4’,
raw: [Object]

}

}

}

Si nous regardons attentivement cette sortie, nous voyons que cela a également une section des événements et elle montre le déclenchement de l’événement voted que nous avons créé dans notre contrat intelligent.

events: {

Voted: {

address: ‘0x59E7161646C3436DFdF5eBE617B4A172974B481e’,

blockNumber: 4257,

transactionHash: ‘0x434aa9c0037af3367a0d3d929
85781c50774241ace1d382a8723985efcea73b3’,

transactionIndex: 0,

blockHash: ‘0x04a02dd56c037569eb6abe25e003a6
5d3366407134c90a056f64b62c2d23eb84’,

logIndex: 0,

removed: false,

id: ‘log_980a1744’,

returnValues: [Result],

event: ‘Voted’,

signature: ‘0x4d99b957a2bc29a30ebd96a7be8e68fe
50a3c701db28a91436490b7d53870ca4’,

raw: [Object]

}

}

Dans l’extrait de code précédent, nous avons extrait la section événements reçus de la transaction que nous avons reçu en réponse à la transaction d’envoi à la fonction de vote de notre contrat intelligent. Comme nous pouvons le voir, la section événements affiche également les valeurs de retour et les valeurs brutes de l’appel de fonction.

Nous sommes maintenant arrivés à la fin de notre exercice de programmation DApp. Dans les sections précédentes de ce chapitre, nous avons développé une application décentralisée de bout en bout sur la blockchain Ethereum et nous avons également déployé une blockchain privée pour notre DApp.

Le DApp peut être utilisé avec le réseau public Ethereum aussi- un électeur doit héberger un nœud et ils peuvent voter en utilisant leurs comptes Ethereum existants sur le réseau public (principal).

Il peut y avoir plusieurs façons dont la logique entreprise dans le contrat intelligent peut être améliorée en utilisant des contrôles et des règles différentes.

Cet exercice de programmation nous donne une idée de base sur la façon d’aborder le développement d’applications décentralisées et les composants qui entrent en jeu au cours du processus. Cet exercice peut être considéré comme un point de départ pour le développement d’applications Ethereum, et le lecteur est encouragé à explorer les meilleures pratiques et des scénarios plus complexes sur le sujet.

Résumé

Dans ce chapitre, nous avons compilé un exercice de programmation de développement d’une application décentralisée basée sur la blockchain Ethereum. Nous avons également appris à mettre en place un réseau ethereum privé et à interagir avec lui à l’aide de la DApp.